基于光谱的40 μm保偏光纤参数测量方法
2020-12-10王少华何沛彤谢良平
王少华,何沛彤,陈 琳,卫 炀,谢良平
(中国航空工业集团公司 西安飞行自动控制研究所,西安 710065)
0 引 言
保偏光纤是通过在光纤中人为引入较大的双折射从而使其具有优异的偏振保持能力,其在光纤传感、光信息处理和光通信领域得到广泛应用。拍长和双折射温度系数是保偏光纤的两项重要参数,表征了保偏光纤的温度性能,对其的准确测量具有重要意义[1-2]。针对拍长的测量,目前有磁光调制[3]、剪断[4]、压力调制[5]、偏光干涉[6]和白光测试法[7]等;针对双折射温度系数测量的报道较少,主要有光栅[8]、偏振串扰分析[9]、布里渊光时域测试[10]和Sagnac干涉测量法[11],测试系统一般比较复杂。
受限于40 μm保偏光纤的器件和设备制作技术,很难通过在市场上直接购买商用光纤器件和设备搭建上述参数测试系统。本文提出通过在一根40 μm保偏光纤上制作基于熔融拉锥技术的晶体包裹型光纤偏振器,将光纤输入端与高偏振度超辐射发光二极管(Superluminescent Diode,SLD)芯片进行45 °对轴耦合,光纤输出端接入光谱仪,搭建了一套简单的偏光干涉装置,从理论上分析了保偏光纤拍长和双折射温度系数的测量原理,并组织实验,通过调制光谱周期与保偏光纤长度的关系实现了拍长测量,通过调制光谱平移量与温度的关系实现了双折射温度系数的测量,验证了理论分析的正确性和方法的可行性。
1 测量原理
图1所示为光谱测量装置示意图,其由高偏振度SLD芯片、晶体包裹型光纤偏振器、光谱仪、待测40 μm保偏光纤和温控装置组成。温控装置用于提供温变环境,保偏光纤的起始端与高偏振度SLD芯片进行α角度对轴耦合,输出端接入光谱仪,在保偏光纤中段的某区域进行熔融拉锥,使拉锥后的光纤最细处<10 μm,此时,拉伸区域的光波基本上不在纤芯中,而是在本身是多模波导的石英芯棒中,然后在锥区最细处采用定向温度梯度法生长双折射晶体[12]。假设双折射晶体的o和e光折射率分别为n1和n2,石英芯棒的折射率为nk,且应满足n1 图1 40 μm保偏光纤参数测量装置示意图 假设高偏振度SLD芯片发出光的横电模(Transverse Electromagnetic Mode,TE)和横磁模(Transverse Magnetic Mode,TM)的光振幅分别为Ex和Ey,SLD与偏振器之间的光纤长度为L,偏振器消光系数为ε,保偏光纤中o和e光的折射率分别为no和ne,那么SLD光源中不同波长λ的光强可表示为 由于不同波长λ会对应不同的光程差2π(no-ne)L/λ,因此,光谱仪接收的光谱会发生周期性调制。为了获得最大的光谱调制对比度,应使α=β=45 °,并采用高偏振度光源。 常温下,假设中心波长附近的两个相邻波长λ1和λ2(λ2>λ1)处于峰值位置,那么它们应满足: 式中,n为干涉级次。由式(2)和(3)可知: 假设未处于和处于温变环境中的光纤长度分别为L1和L2,光纤总长度为L=L1+L2,当初始温度为T1时,中心波长附近的波长λ1处于调制光谱的峰值位置,那么λ1应满足: 当温度升高到T2时,若温度的变化量足够小,满足因温度变化导致的调制光谱不会出现跨条纹平移,原调制光谱的峰值波长将由λ1平移到λ2,λ2满足: 综合式(5)和(6),温度为T2与温度为T1时的(no-ne)的差值为 式中:k为峰值波长随温度的平移速率;K为双折射温度系数。因此,只要能获得k,就可计算出K。 实验中SLD芯片选用850 nm波段高偏振度光源芯片,30 mA正常驱动电流下其偏振度约为12 dB,中心波长为843 nm,双折射晶体选用硝酸钠(NaNO3)晶体,待测光纤为北京玻璃研究院提供的850 nm波段40 μm保偏光纤,光谱仪选用Agilent 86140B 型光谱分析仪,最小分辨率为0.01 nm。温控装置是一台具有精确温控功能的加热台,温控精度为±0.2 ℃。 首先,在待测光纤的中段位置制作晶体包裹型光纤偏振器;然后,将光纤输入端与SLD芯片进行45 °对轴耦合,光纤轴向通过高倍显微镜观测光纤端面确定,耦合通过三维调节架实现;最后,将光纤输出端接入光谱仪,旋转与SLD芯片对接侧的拉锥光纤角度,使调制光谱获得最大对比度。 根据理论分析可知,SLD芯片与偏振器之间光纤长度的测量精度决定了拍长测试精度,由于制作偏振器时需要对光纤进行熔融拉伸,拉伸区的光纤双折射会随着拉伸直径变小而逐渐变小,因此,不能直接测量制作好偏振器后晶体根部与SLD芯片之间的光纤长度,在实验中,测量拉伸光纤在拉伸前的中点到SLD芯片之间的光纤长度作为有效长度。 为了提高拍长测试精度,实验中通过改变SLD芯片与偏振器之间的光纤长度来获得不同光纤长度与调制光谱周期之间的多组测试数据,由式(4)可知,调制光谱的周期与光纤长度的倒数呈线性关系,因此,可以先利用线性拟合获得比例系数,再根据式(4)计算出拍长值来提高测量精度。表1所示为实测光纤长度与调制光谱周期数据,其中调制光谱周期取中心波长附近5个调制周期的平均值。 表1 光纤长度与调制光谱周期测试数据 图2 调制光谱周期随光纤长度倒数的变化关系曲线 实验中SLD芯片与偏振器芯片之间的保偏光纤总长为193.0 cm,将中间40 cm的保偏光纤(即L2=40 cm)固定到加热台上,控制加热台从25 ℃开始以0.5 ℃/min的升温速率加热到75 ℃,每2 ℃记录一次光谱数据,此条件下测量的调制光谱没有发生跨条纹移动,图3(a)所示为25和27 ℃下光谱仪记录的调制光谱数据,图3(b)所示为局部放大图。25 ℃下的某级峰值波长A点(854.4 nm)平移至27 ℃下的B点(853.9 nm),通过始终追踪测量该峰值波长就可计算出波长随温度的平移速率。 图3 25和27 ℃下调制光谱图 图4所示为上述峰值波长随温度变化的关系数据和线性拟合后的曲线。由图可知,随着温度的逐渐升高,峰值波长近似线性地向左平移,线性拟合函数为y=-0.279 25x+861.4,斜率k=-0.279 nm/℃,代入式(8)可得双折射温度系数为-4.2×10-7/℃。 图4 某峰值波长随温度变化的关系曲线 针对40 μm超细径保偏光纤拍长和双折射温度系数存在测试装置搭建困难和测量精度低的问题,本文提出了一种基于调制光谱的双参数测量方法,通过在线制作偏振器和光源耦合,搭建出一套简单的偏光干涉装置;分别从理论分析和实验组织两个层面对测试方法进行了阐述和验证。本文虽然是针对40 μm保偏光纤提出的测试方法,但同样适用于其他更细直径和商用的80 μm及以上直径的保偏光纤参数测量,且测试装置搭建将会更加简单。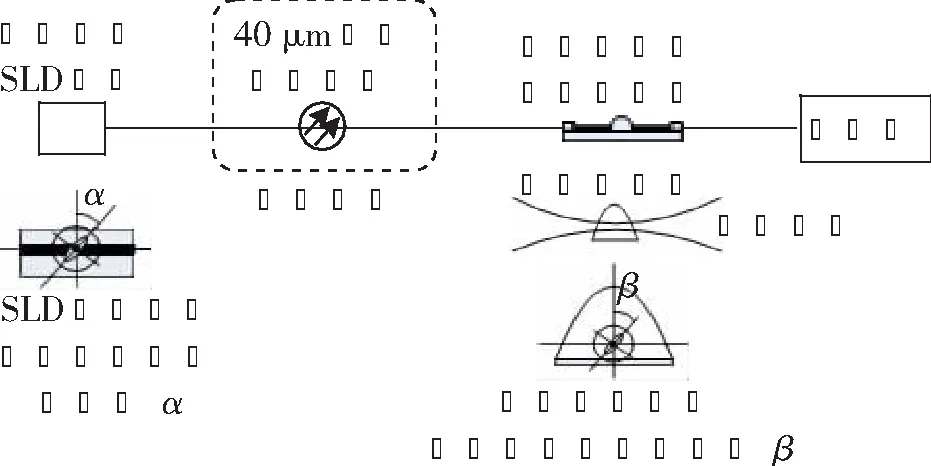

2 实验研究
2.1 拍长测量

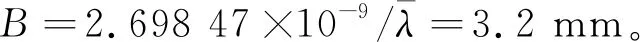

2.2 双折射温度系数测量


3 结束语
