基于WM/C的牛头刨床六杆机构运动特性研究

王智森，韦洪新

(景德镇学院 机械电子工程学院，江西 景德镇 333000)

牛头刨床因滑枕和刀架形似牛头而得名，刨刀装在滑枕的刀架上作往复运动，多用于切削各种平面和沟槽[1-4]。刨刀切削运动的模型可以简化为由摆动导杆机构和导杆滑块机构组合而成的六杆机构，因此，从保证工作精度，缩短空行程时间的角度，研究牛头刨床六杆机构的急回运动特性尤为重要[5-8]。为了使刨刀工作行程中速度尽可能平稳、均匀，传统设计采用的经验法或试凑法耗时长、成本高且精度低，难以保证工作行程中速度的稳定性和系统的可靠性[9-10]。

在已知机构尺寸及原动件运动规律的情况下，可以推导出其余构件上各点的轨迹及位移、速度、加速度方程。不论是设计新的机器，还是为了了解现有机械的运动性能，这些要素，都是十分必要的，而且这也是研究机械动力性能的必要基础和前提[11-12]。对于牛头刨床来说，其刨刀在有效工作行程中应该接近等速运动，且回程速度应高于前者速度，从而提高效率[13]。为了确定牛头刨床的设计是否满足要求，就必须对其进行运动分析。

本文结合Working Model与C语言编程对牛头刨床六杆机构模型进行简化，添加尺寸约束、几何约束分别确定各连杆外形轮廓尺寸、运动副以及驱动，对简化模型进行运动特性分析，得到刨刀位移、速度和加速度变化规律曲线，并通过C语言编程程序执行结果加以验证。该仿真分析方法为降低机床的设计成本和提高机床的工作精度提供了有效手段。

1 牛头刨床六杆机构模型建立

将牛头刨床六杆机构模型进行简化，画出其运动简图如图1所示，结构组成为：原动部分是电机，传动部分是齿轮、曲轴连杆机构，执行部分是滑枕，控制部分是离合手柄、变速控制手柄等。其中自由构件数n=5，低副数Pl=7，高副数Ph=0，故自由度F=3n-(2Pl+Ph)=1。

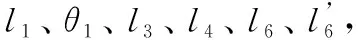
(1)

将矢量方程变换成投影方程为：

(2)

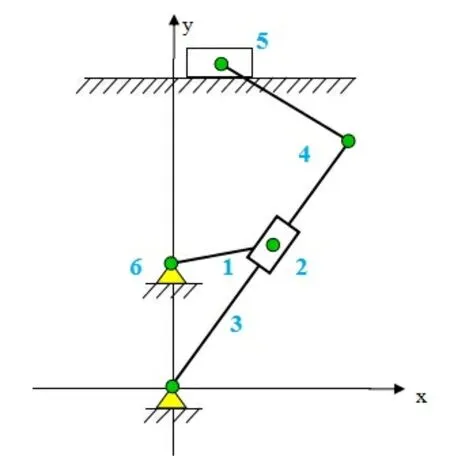
图1 牛头刨床六杆机构运动简图

根据投影方程设定牛头刨床六杆机构的参数为：曲柄1尺寸l1=100 mm，导杆3尺寸l3=300 mm，连杆4尺寸l4=150 mm，机架6尺寸l6=150 mm。利用Working Model软件导入机构参数，为便于分析和计算，整体放大20倍，建立的简化模型如图2所示，其中滑块与导杆、刨刀与床身之间为滑动杆连接，其余为销钉连接。

图2 牛头刨床六杆机构简化模型

Working Model软件在2D环境下为利用复杂的编辑功能来提供一个完整的专业的动态模拟，可以模拟牛顿运动力学上的机构，并且提供一些简易的图解让设计者更容易从事实验及分析不同的运动情况。本文利用Working Model的建模、仿真功能，对牛头刨床六杆机构进行虚拟设计和运动分析，直观、便捷、高效地得到相关参数，利于机构优化设计。

2 牛头刨床六杆机构运动分析

在建立的牛头刨床六杆机构简化模型的基础上，设定曲柄1的转速参数为n1=50 r/min，逆时针转动，利用Working Model软件模拟仿真牛头刨床切削加工过程，得到刨刀的工作行程轨迹及导杆、连杆连接处的运动轨迹，如图3所示，图中白色细线为运动轨迹线。

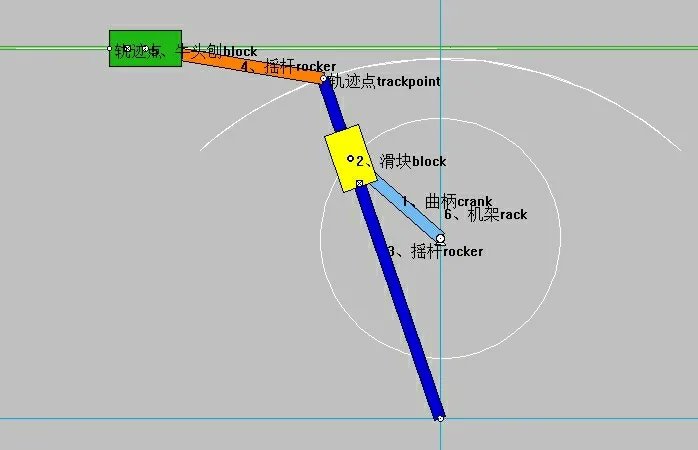
图3 刨刀工作行程轨迹

用Working Model软件实时求解，得到刨刀位移、速度及加速度等相关运动参数随时间变化的曲线，便于让设计者直观地了解和捕捉到牛头刨床六杆机构的运动规律。仿真得到的各项数据为机构尺寸的优化设计提供了参考。

2.1 刨刀位移曲线分析

刨刀的工作行程可以通过由刨刀和床身组成的滑动副位移来测量。在Working Model建立的机构简化模型中选择该滑动副，通过滑动副添加刨刀的轨迹点，该轨迹点记录了刨刀位移随时间变化的曲线，如图4所示。从刨刀位移曲线图中可以直观读取一次切削周期内，刨刀工作行程的范围。由此分析得出牛头刨床单刃刨刀加工，且在滑枕回程时不切削，刨刀工作行程平稳。

图4 刨刀位移曲线

将公式(2)进行整理化简得如下方程：

(3)

将整体放大20倍的机构各项参数代入公式(3)，以曲柄1的θ1从0°～360°为一个周期，通过C语言编程得到刨刀位置程序，如表1所示。

将程序输出的位置结果绘制成刨刀位移曲线，如图5所示，该曲线与Working Model仿真结果完全拟合。

表1 刨刀位置程序

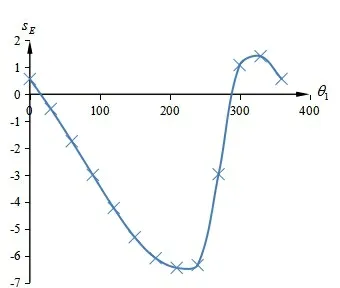
图5 C语言实现的刨刀位移拟合曲线

2.2 刨刀速度曲线分析

用上述方法，选择刨刀和床身组成的滑动副创建速度函数，用Working Model仿真得到刨刀速度曲线，如图6所示。

图6 刨刀速度曲线

从刨刀速度曲线图中可以看出：在0.25 s和3 s两个时刻，刨刀的速度为0，分别处在位移的两个极值上。0.25～3 s，刨刀向左移动，切削工件；3～3.75 s，刨刀向右回程。分析可得：牛头刨床刨刀工作行程的平均速度、速度波动明显小于回程的平均速度、速度波动，切削运动平稳，验证了Working Model运动仿真结果的正确性。在牛头刨床刨刀工作行程中，速度较为平稳，近似于等速，这样能够保证刨刀的工作精度和使用寿命。

将位置方程对时间取一次导数，得到速度方程式(4)。

(4)

经过化简整理得：

(5)

利用C语言编程，可以得到刨刀速度程序(见表2)。将程序输出的速度结果绘制成刨刀速度曲线，如图7所示，该曲线与Working Model仿真结果接近拟合。

2.3 刨刀加速度曲线分析

同理上述分析过程，选择刨刀和床身组成的滑动副创建加速度函数，用Working Model仿真得到刨刀加速度曲线，如图8所示。

表2 刨刀速度程序

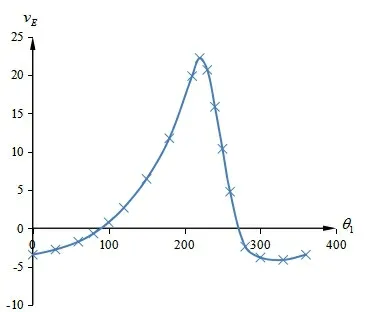
图7 C语言实现的刨刀速度拟合曲线

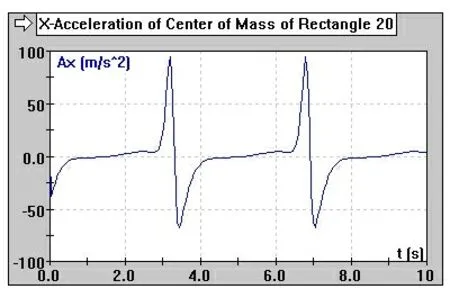
图8 刨刀加速度曲线

由刨刀加速度曲线图分析可得：牛头刨床在回程时速度变化很快，验证了牛头刨床的急回特性，这个特性提高了切削工件时的生产效率。通过设定曲柄不同的转速值，比较刨刀位移、速度、加速度分析结果发现：在电机转速改变的情况下，牛头刨床刨刀的速度和位移曲线变化不大，刨刀加速度曲线变化较大。基于此规律，设计者可以根据调试牛头刨床六杆机构尺寸参数和电机转速参数设计满足切削加工要求的最优值。

将位置方程对时间取二次导数，得到加速度方程式。方程式如下：

(6)

通过C语言编程得到刨刀加速度程序，如表3所示。将程序输出的加速度结果绘制成刨刀加速度曲线，如图9所示，该曲线与Working Model仿真结果接近拟合。

图9 C语言实现的刨刀加速度拟合曲线

表3 刨刀加速度程序

3 结论

研究牛头刨床六杆机构运动特性的软件工具很多，本文联合Working Model与C语言软件对牛头刨床六杆机构的运动特性进行了仿真与验证，该方法操作简便、直观，省去了三维建模的繁琐过程，运动分析结果输出实时、高效，优化效率相比传统设计采用的试凑法和解析法提高了20%。利用该方法，设计者根据所需切削加工要求可以实时修改机构形状、尺寸参数，得到最优值方案。