自适应模糊PID控制超声波电机研究

甘家梁,熊曾刚,刘桂涛,郭海如

(湖北工程学院 计算机与信息科学学院，湖北 孝感 432000)

超声波电动机(Ultrasonic motors，USM)由于体积小巧，重量轻，噪声低，惯量低，响应速度非常快，具有高精度和纳米级分辨率及在断电状态下能自我锁定、不存在电磁辐射等优点，因此在许多高科技领域中得到了广泛的应用[1-2]。由于USM工作特性是一个非线性时变系统，它不仅会受到驱动电源电压的大小、频率、相位差以及工作环境的影响，并且随着电机运转时间的增长，温度也会随之升高，这会影响电机转子与定子摩擦层参数的变化[1-3]，单个的PID控制器或模糊逻辑控制器(Fuzzy Logic Controller，FLC)控制USM，难以达到生产过程中良好的控制效果，因此提出了自适应模糊逻辑PID控制器控制超声波电机。

设计的自适应模糊PID控制器，在PID控制系统中引入模糊逻辑控制法则，用于建立参数KP、KI和KD之间的二元连续函数，根据速度输入的误差信号e、误差信号变化ec和误差信号的变化率de(误差信号的二阶导数)的隶属度函数，能够在线调节KP，KI和KD参数，自动实现PID各个参数的最优调整，补偿PID增益不好的区域来提高PID的控制性能，既可以发挥模糊控制良好的动态响应，快速达到稳定和超调量小的优势，又可以增强FPID控制器的能力，以便很好地捕获超声波电机驱动系统的非线性，以适应超声波电机在不同的运行条件下，提高控制系统处理具有高度非线性过程的能力，改善电机压电驱动机构中定子与转子之间接触的摩擦效应引起的温度变化、负载扰动等参数不确定性。这是实现模糊自适应PID控制器设计的关键。

在Matlab环境下，采用简化的超声波电机混合模型，对所提出的控制器的性能进行了仿真评估。达到了电机的动态性能的需要，效果明显优于单个的控制器。最后，自适应模糊PID控制器在实验条件下，应用于型号规格为GTUSM-60-R-A的USM，效果符合要求。

1 模糊PID控制USM系统设计与仿真

1.1 构建超声波电机的仿真模型

为了更好地对超声波电机进行应用研究，首先需要解决的问题是构建超声波电机的数学模型[4-5]。其次，由于 USM 为阻容性负载，需要设计一个体积小且能满足控制系统性能要求的驱动器[6]。根据文献[7-8]，参照型号为GTUSM-60-R-A的行波型超声波电机出厂参数和其定子模型和旋转运动模型，获得一个行波型USM 的等效模型，图1为简化的超声波电机混合模型。

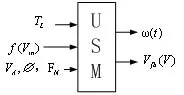
图1 简化的超声波电机混合模型

在图1中，简化的USM输入输出混合模型共有5个输入端和2个输出端。其中有2个主要输入端口：负载转矩TL(0～0.3 N·m)和驱动信号f(vin(t))，其频率为40～42 KHz，其他输入端信号为常数：加在电机两端的电压为VA=100 V，相移∅(π/2)和法向力FN(160 N)的振幅。2个输出端口是电动机速度ω(t)和一个与驱动行波信号A幅度成比例关系的反馈信号电压Vfb(V)。

1.2 模糊PID控制USM系统设计

在USM的控制过程中，传统的模糊PID控制器仅使用误差E和误差变化EC作为输入来满足不同时刻的自调节PID参数要求，这样解决了多变量模糊控制规则的数量爆炸式增长问题，得到了更大的可控范围。然而，当USM控制系统的输出进入稳态近似阶段时，这种模糊PID控制的稳定性将下降，并且控制器将无法产生误差信号以消除这种不稳定性。此时，如果将误差的变化ec改为误差的加速度变化de(误差的二阶导数)作为模糊PID控制输入，则使系统具有良好的稳定精度。但是，规则的增加肯定会增加控制算法的难度，并影响控制对象的响应速度。

鉴于上述分析，为了有效地利用模糊控制器解决传统PID控制器不能快速响应和稳定的问题，提出了一种基于新的模糊控制规则在线调整PID参数的控制器，控制原理如图2所示。其中，ω*是控制系统需要的参考速度，ωfb是USM输出的反馈速度，G0和G1分别是速度误差e及其微分de归一化因子，G2和G3去归一化因子。提出的模糊逻辑推理系统包括三个主要处理过程，即输入数据的量化过程，任务是根据需要对G0和G1进行调节，得到量化的论域；模糊逻辑控制过程，建立模糊规则库，确定模糊关系，进行推理和去模糊化；最后是对模糊控制增量进行归一化处理，通过因子G2和G3完成去归一化过程和控制变量dVin的整合。

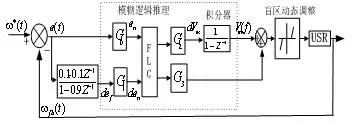
图2 模糊PID控制系统框图

速度误差信号ω(t)=ω*(t)-ωfb(t)。 模糊PID控制器的输出变量为vin(t)，转换为驱动频率以应用于超声波电机驱动系统。

模糊PID结构设计完成后，针对输入输出模糊变量设计模糊归属函数。表1给出了组合输入语言变量论域，根据专家实验经验建立的模糊规则库和输入/输出隶属函数关系。

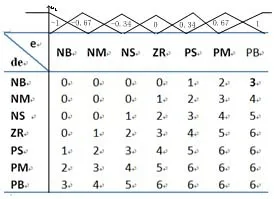
表1 组合输入变量论域，模糊规则库和(输入/输出)隶属函数

应用Mamdani推理，模糊控制语言变量的一条模糊规则R表示如下：

R(J):If {e is ZR and de is NS} then {dVin is NS}

(1)

式中：e为语言输入变量速度误差，de为速度误差变化值，在这个特定的规则中分别使用语言变量值ZR和NS与之对应。最后，模糊控制的输出由重心方法确定。

模糊PID控制输出vin(t)和模糊PID增益的等效控制表达式由方程式(2)给出：

(2)

式中：G0， G1，G2和 G3前面已经定义， dVin=PKPe+DKdde/dt，D和P是模糊变量的量化级别，分别与e与de相对应，根据表1，D和P的基本域分别为[-1，0.34]和[0.34，1]。

1.3 仿真与分析

为了验证所提出的行波型超声波电机的控制方案，应用图1的USM混合模型。用仿真软件Matlab进行了该控制方案的仿真对比实验。把归一化增益参数设置为G0=0.5，G1=0.01，去归一化因子设置为G2=250和G3=100，转矩T1=0.3 N·m，采样时间=77 μs，未知的扰动由Matlab函数库中的randn函数模拟给出，仿真结果如图3所示。

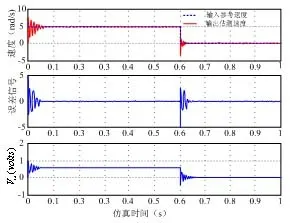
图3 USM动态仿真图

由图3的仿真结果可知，当输入的参考速度为5 rad/s时，输出的响应速度，在到达稳态值时，出现了明显的振荡，振荡幅度在2.5～7.5 rad/s之间，超调量δ=50%，即超调量明显较大；速度的响应到达稳态值的时间为ts=0.05 s，比较长，动态响应效果并不是很好。

2 自适应模糊控制系统设计

2.1 自适应模糊控制系统设计

为了改善模糊PID控制器控制USM的瞬态响应，对图2进行了改造，设计了一个自适应模糊PID控制器，增加了一些在线调整元素，如图4所示。 一些控制增益因子可以通过自适应技术，在实际速度的作用下进行自调整，以便改善动态响应。

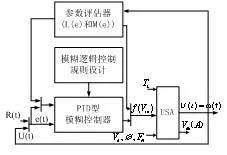
图4 自适应FPID控制系统图

由图4 可知，改造的自适应控制系统由一个实时速度ω(t)的反馈输入端和两个控制因子的输出端的参数评估模块组成。

自适应调整算法由方程(3)给出。

(3)

式中：G2a=G2a，G1c=G1c， 增益 a， c， L(emin)和M(emax) 是相对于稳态和瞬态状态调整的常数。L(e)和M(e)可以用误差[emin，emax]粗略调整，以获得具有良好的扩展调谐区域。

为了消除稳态误差，需要调整模糊控制的过程变量与控制输出变量，得到调整后的输出隶属度函数如图5所示。

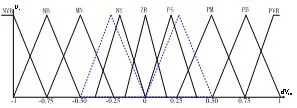
图5 输出隶属度函数

也就是说，通过调整隶属函数和扩展比例因子的自整定区域，可以提高系统的稳定性，改善控制系统的动态响应。

2.2 仿真和实验结果

为了验证所提出的自适应模糊PID控制器控制行波型USM的控制方案，在Matlab/simulink环境下，构建了简化的USM混合模型仿真系统，获得的仿真结果如图6所示。与图3相比，图6具有良好的阻尼响应，响应时间小于25 ms，输出的响应速度跟踪效果良好，显示出动态响应得到显著的改善。

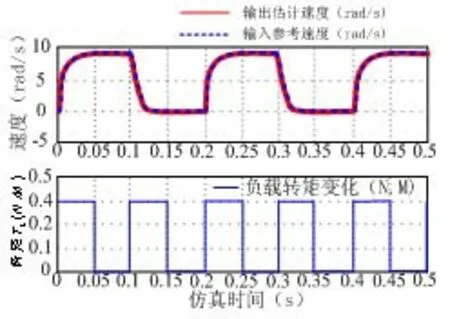
图6 自适应FPID控制器在不同的工作条件下的仿真效果

为了进一步对所提出的控制方案进行验证，使用Shinsei USR 60TWUSM，其参数如下：驱动电压为100 V，驱动频率为40 KHz，额定输出功率为4 W，额定转矩为0.32 N·m，额定转速为10 rad/s。设计了基于计算机的自适应模糊逻辑PID控制系统，并制造了超声波电动机驱动系统。 在不同负载条件下，负载转矩在0和0.3 N·m之间，测量了电动机的正转和反转速度的动态性能。实验结果如图7所示，示波器的速度刻度调节到20 rad/s，输入的参考速度设定为-8～+8 rad/s。图7A 是模糊PID控制器控制USM的观测结果，可以看出，测量速度明显滞后于输入的参考速度值，并有速度振荡存在；图7B是应用自适应模糊PID控制器控制USM的观测结果，可以看出速度跟踪效果得到显著改善，并且匹配较好；图7C为精细调整自适应控制系统中增益因子G2的响应情况，可以看到跟踪可以完全匹配，意味着调整增益因子G2，可以处理具有极端非线性和参数不确定性的系统。通过实验验证了所设计的控制器对环境的适应性强，并且鲁棒的平衡性能良好。

3 结论

本文采用模糊自适应PID控制方法，通过模糊推理在线调整控制变量的输出，以弥补PID增益不佳的区域，减少了USM系统的响应时间，同时减少了超调量，最终改善了稳态表现。本文详细描述了USM上的自适应模糊PID控制器实现过程。所提出的控制器的控制方案，其显著特性是不需要受控设备的精确模型，并且设计过程简化。基于Matlab的仿真和实际控制效果表明，该控制器不仅鲁棒性良好，且与传统控制器相比，还具有良好的动态和稳态特性。

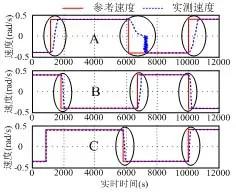
图7 示波器观测的自适应模糊PID控制USM速度响应图