测量高度对盐碱土光谱响应的对比分析研究
2020-12-10任建华臧淑英
隋 敏,任建华,陈 强,赵 悦,臧淑英
(哈尔滨师范大学 寒区地理环境监测与空间信息服务 黑龙江省重点实验室,黑龙江 哈尔滨 150025)
0 引 言
土壤盐碱化是一定的气候、地形及水文地质等自然条件对土壤水、盐运移产生作用的结果[1],随着人口的迅速增长和人类的不合理活动,土壤盐碱化程度日益加剧并降低了土壤肥力,这直接影响到植物生长,导致作物产量下降[2]。据统计,盐碱化土壤占世界陆地总面积的6.5%,其中尤以印度恒河平原、亚马逊平原东北部等地区最为严重[3]。我国盐碱化土地面积约为0.35亿hm2,主要分布在东北松嫩平原、西北干旱半干旱地区、黄淮海平原以及东部沿海地区[4]。因此,及时获取土壤信息,针对土壤盐分进行高效的分析监测对解决区域土壤盐碱化问题具有重要意义。
20世纪70年代起,国外学者开始将卫星遥感应用于土壤盐碱化的监测,到90年代日趋完善。21世纪以来,随着技术的不断发展,拥有精细光谱分辨率、纳米级连续光谱的光谱遥感实现了对盐碱化土壤快速、无损的测量[5]。其中,利用遥感手段所获取的土壤反射率数据被广泛应用于土壤盐分评估模型的建立。Chen等[6]利用Landset7 ETM+与Landset8 OLI数据提取反射光谱,通过改进后的植被指数来判别土壤盐碱化程度,并在此基础上建立了中国黄河三角洲垦利区的季节SCC反演模型,发现了长三角盐碱化土壤的季节盐分动态变化过程并绘制了土壤盐分季节变化图。Moreira等[7]将混合光谱分析应用于Landset8 OLI与Hyperion遥感影像,他们使用盐度指数对比分析了两种影像在对巴西东北部盐碱土与非盐碱土的识别能力,结果表明Hyperion遥感数据对土壤盐分的估算误差更小,识别精度更高。Nawar等[8]借助Landset7 ETM+数据与土壤电导率重建了土壤反射光谱,利用偏最小二乘回归与多元自适应回归样条模型来估算埃及西奈半岛埃尔蒂娜平原土壤盐分,结果表明多元自适应回归样条模型R2达到了0.70,模型精度高,适合高盐地区土壤盐分的估算与制图。Elhafyani等[9]利用Landset8 OLI数据与土壤电导率构建了摩洛哥的塔菲拉勒特平原土壤盐度指数的多元线性回归模型,结果表明不同波段的模型精度较高,决定系数R2在0.53~0.75间,表明该方法在此研究区具有一定的适用性。再屯古丽·亚库普等[10]针对中国新疆于田绿洲利用四极化ALOS-2 及PALSAR2数据,使用多元回归模型、地理加权回归模型、BP神经网络模型建立了土壤含盐量、含水量及pH值的雷达后向散射系数定量反演模型,结果表明三层BP模型盐分反演精度最高,RPD达到5.53。
除从航空和航天遥感平台上获取高光谱数据外[11],地面光谱仪作为一种重要的数据获取手段,也被广泛用于与遥感数据进行比较验证及土壤理化性质的定量分析等研究当中。地基高光谱测量实验主要包括室内测量与室外测量两种类型[12-14]。其中,室内测量实验主要指在光学暗室条件下,利用光谱仪传感器镜头照射土样来获取光谱数据,一般测量高度以近土壤表面为主;室外实测中测量高度主要取决于地面植被覆盖状况,同时还受土壤表面状况、天气条件及研究尺度等诸多因素的影响[4]。Farifteh等[15]在荷兰特赛尔岛田间采集粉砂质黏土、砂壤土、沙土三种质地不同的盐碱化土壤,在暗室利用ASD光谱仪设置实验高度3cm获取土壤光谱数据,比较不同质地的土壤的盐碱化程度及其光谱信息,结果表明随着土壤中盐分浓度的增加,波段在1 300nm以上观测到的吸收特征变宽,最大反射率位置向短波长方向偏移,总反射率呈比例变化。Srivastava等[16]在印度哈里亚纳邦稻麦种植区获取盐碱土,在暗室内使用ASD光谱仪设置实验高度5 cm获取数据,分析表明土壤盐分在光谱1 390 nm~2 400 nm区间对盐度变化最为敏感,反射率一阶微分处理后的偏最小二乘模型对土壤盐分的预测精度R2达到0.93。Luis等[17]在巴西北部灌溉盐碱土,获取土样暗室,并在内使用ASD光谱仪在7 cm高度下对比测量了原始土壤以及加入石膏后土样含盐量的光谱响应,研究结果表明石膏对灌溉区盐碱土的改良效果明显。Fu等[18]以中国新疆天山准噶尔盆地为研究区,使用ASD光谱仪采集15 cm下室外土壤样品的光谱数据,并结合粒子群优化概率神经网络模型对土壤盐分进行定量分析,进而区别和判定人类活动在研究区内的不同干扰强度对盐碱土的影响。Lin等[19]将SVC光谱仪在室外测量了10 cm实验高度下的土样光谱,同时结合HJ-1A卫星遥感影像建立了最佳土壤盐碱化反演模型,并用此模型实现了大尺度下松嫩平原北部扎龙湿地土壤盐分与pH值的高精度定量反演。Bouaziz等[20]在突尼斯东南部土壤表面8 cm距离上,收集了土壤样本的光谱数据,同时结合该区域的Landset影像,并对数据进行了主成分分析与集群分析处理,以期提供有关多光谱数据与地面真实性之间相互关系的大量信息,从而有助于更好地理解多光谱数据与地面实况测量之间的相互关系,实现对受盐污染土壤状况的监测。
从现有研究来看,虽然地面实测光谱实验更有针对性,且反射率数据在采集过程中受干扰也较少,但大多的地面实测光谱实验都是在某一固定高度下进行,所获取的光谱数据仅作为地面参考数据与遥感影像进行比较或者直接加入到模型中进行运算研究,而较少考虑光谱实验中实验高度对测量结果的影响。因此,本研究从室外实测光谱实验入手,通过确定不同的光谱测量高度,定量研究不同测量高度下土壤含盐量对光谱响应的差异,在此基础上寻找特征谱段并建立合理的土壤盐分预测模型,通过对光谱分析与模型结果的对比,以期优化松嫩平原苏打盐碱土光谱实验方法,针对后续实验操作中测量高度的确定提供参考建议,从而能够更好的提高土壤含盐量的预测精度,为东北松嫩平原土壤盐碱化改良提供准确的数据支持。
1 材料与方法
1.1 研究区概况
松嫩平原不仅是世界三大苏打盐碱土集中分布区之一,也是我国土壤盐碱化最严重的地区之一[21]。该区域土壤低洼部分堆积了近代湖相粘质和细砂质沉积物,且土壤质地粘,渗透性差,使得土壤pH值普遍在8.5以上,属于中度或重度盐碱土[22]。本文选取吉林省白城市为研究区,该区域属于温带大陆性季风气候,年降水量为400 mm~500 mm,年蒸发量达到1 200 mm,较高的蒸发降水比加上剧烈的人类活动干扰使得土壤盐碱化现象日趋加剧,是典型的重度盐碱土分布区域。
1.2 土样采集与处理
为保证采集的土壤样本的均质性,本研究于2018年10月至11月,利用网格法采集土壤样本共计56个,采样范围在44°13′57″~46°18′46″N,121°38′35″~124°22′50″E之间,取样深度为0~20 cm之间,研究区采样点示意图见图1。对采集回来的土壤样本进行的烘干和研磨后,统一过80目筛以剔除土壤样本中的杂草和植物根系,用于后续的土壤理化性质测定和光谱采集。实验室内使用电导仪DDB-303A结合电导法测定土壤样本的EC值,使用LPII5PHMeter结合酸度计法测量土壤样本的pH值。
1.3 光谱数据测量与处理
本研究采用SVC-HR1024i便携式地物光谱仪对土壤样本进行光谱数据测量,其有效光谱范围是350~2 500 nm,其中350~1 000 nm的采样间隔为3.5 nm、1 000~1 850 nm的采样间隔为9.5 nm、1 850~2 500 nm的采样间隔为6.5 nm。光谱采集实验在上午11时至下午1时的连续晴朗无云的天气条件下进行,土壤样品放置于尺寸为直径4.6 cm、高度3 cm的黑色圆柱形铝盒内,铝盒内装满土样并稍稍刮平,使其表面平整,放置于黑色的15 cm×15 cm的正方形升降台中心上,选取25°镜头光纤测量,实验高度3 cm测量对应的照射面积为9.14 cm2;实验高度4cm测量对应的照射面积为16.75 cm2;实验高度5 cm测量对应的照射面积为26.17 cm2;实验高度6 cm测量对应的照射面积为37.68 cm2;实验高度7 cm测量对应的照射面积为51.29 cm2;在考虑到光纤镜头的照射面积以及铝盒的土样面积下,本研究最终选取3 cm、4 cm、5 cm、6 cm、7 cm等5个不同高度对土壤光谱数据进行测量,探头保持垂直向下正对铝盒,每次测量保证铝盒在升降台位置不变,精准控制测量高度的变化。为每个样本均进行重复测量20条取平均值作为最终的光谱反射曲线,并将光谱间隔重采样为1 nm。
由于光谱数据的低阶微分处理对噪声的敏感性低,因此为了达到更好地反演效果并突出光谱的混合特征信息,本研究对Savitzky-Golay平滑处理后的数据利用公式(1)公式(2)对原始光谱进行一阶微分与二阶微分的数学变换[23]。
(1)
(2)
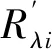
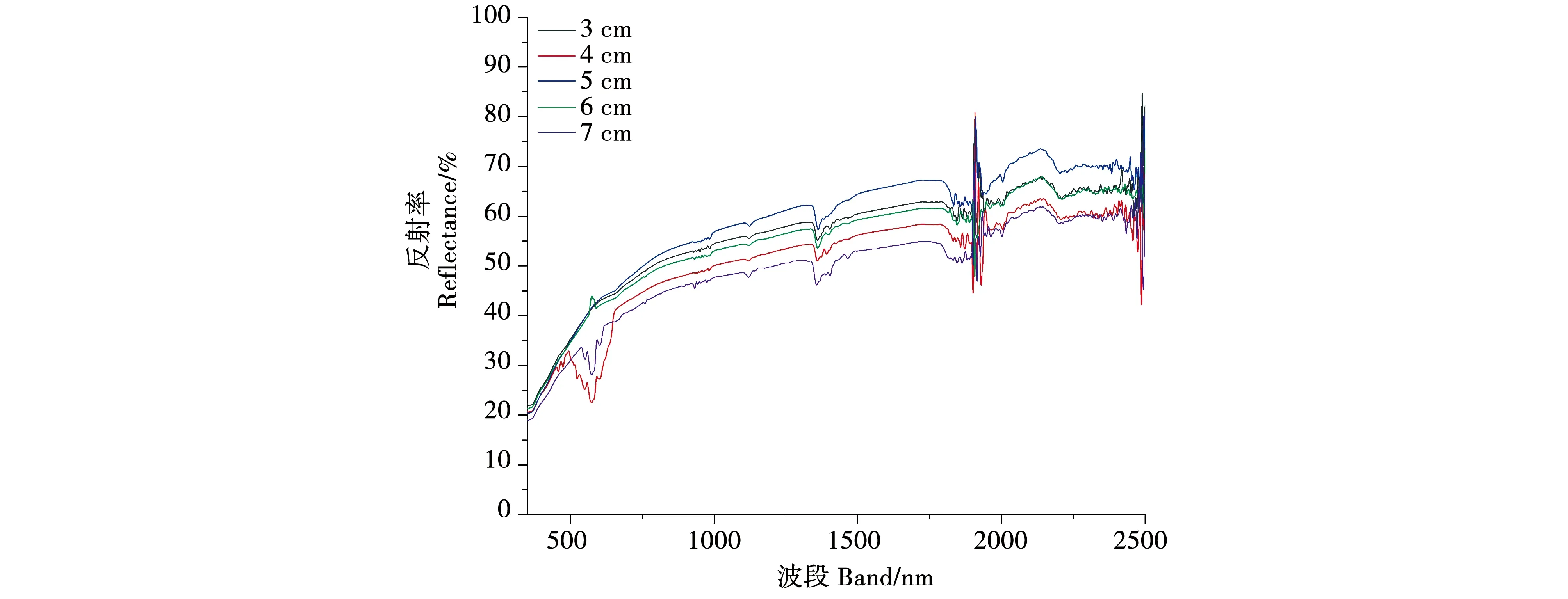
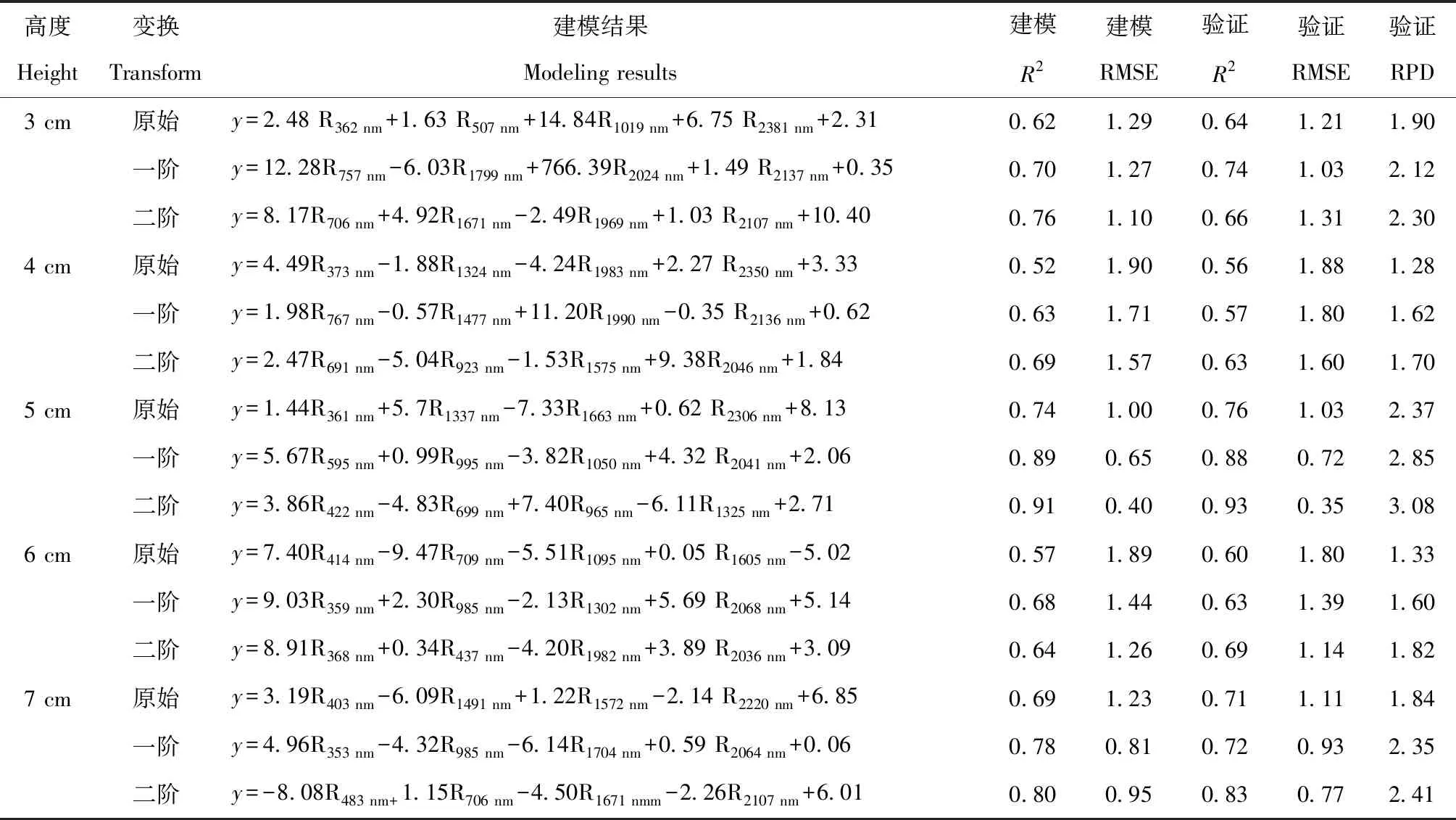
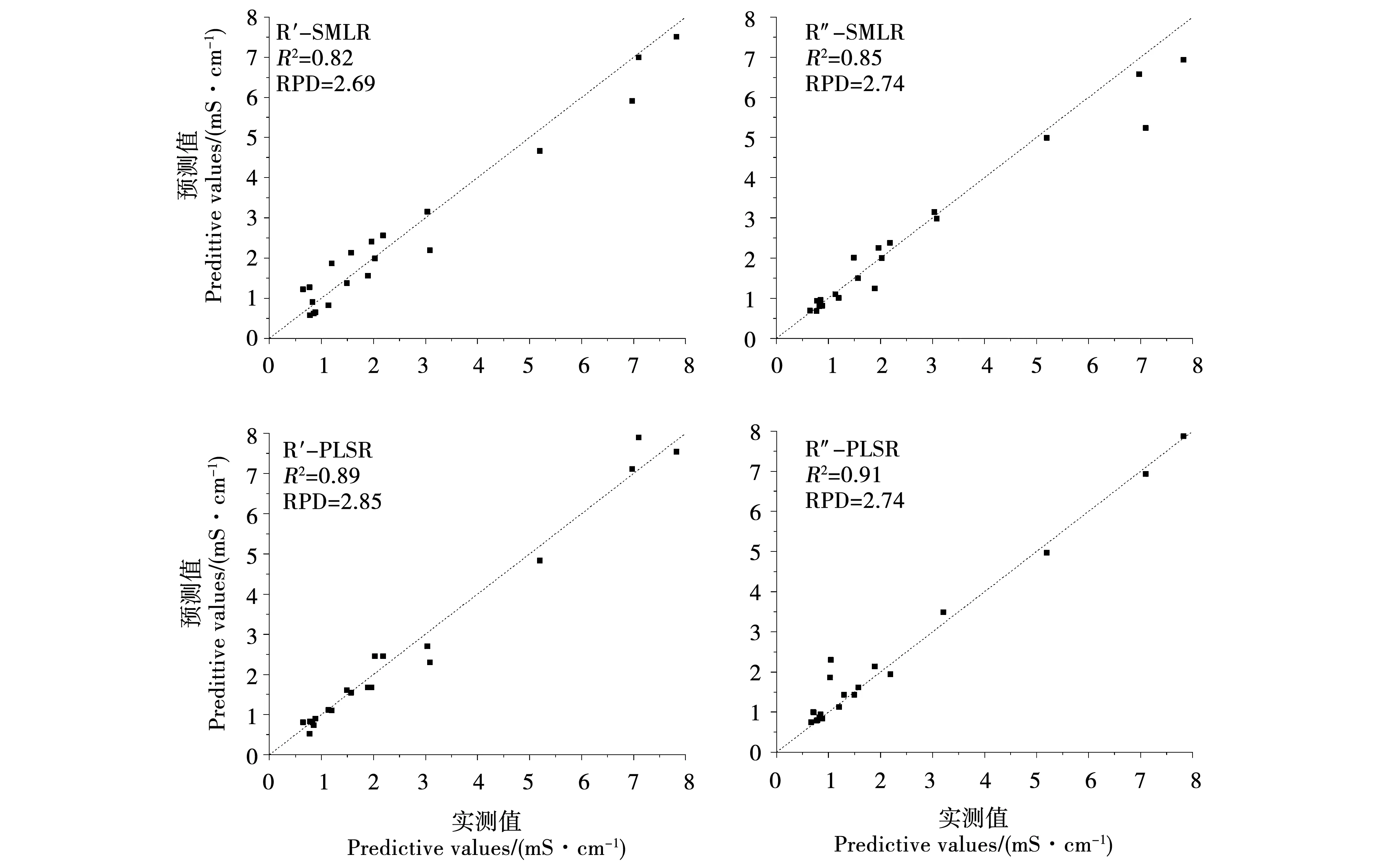
对处理后的敏感光谱波段数据带入到多元线性模型与偏最小二乘模型中进行分析运算,基于土壤盐分EC的实测值和模型结果的预测值来计算评级指标。估算精度通过决定系数R2、均方根误差RMSE、相对分析误差RPD这3个指标进行衡量,模型的R2越大,RMSE越小,模型估算准确度越高;反之越差。当RPD>2时,模型预测精度极佳;当1.4 R2=∑ni=1(Y^-Y-)2∑ni=1(Yi-Y-)2RMSE=∑ni=1(Yˊ-Y)2nRPD=SDP(∑ni=1(Yˊ-Y)2-{[∑ni=1(Yˊ-Y)]2/n}/n-1)1/2SDP={∑ni=1Yˊ2-[(∑ni=1Yˊ)/n]/(n-1)}1/2 对56个样本的电导率与pH值进行统计分析的结果如下表1所示。模型计算得出,土壤样本的电导率平均值为1.89 mS·cm-1,标准差为1.78 mS·cm-1,变异系数为94%。土样的pH值最小为8.39,最大值达到10.8,变异系数为4.7%。分析结果表明研究区内所采集的56个样本的盐分含量较高,并且盐分变异系数大,能较好的反映该地区的苏打盐碱土的盐分状况。 表1 土样电导率与pH值统计分析结果Table 1 Statistics of conductivity and pH of soil samples 根据样本EC值的范围,选取EC值的中值的9号样本作为代表样本,展示3 cm、4 cm、5 cm、6 cm、7 cm这5个实验高度下代表样本的原始光谱反射率在不同实验高度下的对应表现,图中光谱曲线经过平滑与重采样1 nm处理(图2)。 图2 代表样本不同实验高度下原始光谱曲线Fig.2 The original spectral curves of samples at different experimental heights 如图2所示,为代表样品在不同实验高度下的原始光谱曲线,样本的原始光谱在波段350~2 500 nm区间内呈现波动上升趋势,实验5个不同高度下波段与反射率的整体趋势保持一致,不同高度的表现差异较小,在350~400 nm、2400~2 500 nm间信噪比较低,与前人研究结果一致[26]。实验高度5 cm下全波段反射率最佳,数值最高。其次为实验高度3 cm、6 cm、4 cm、7 cm。原始光谱波段反映了不同实验高度下光谱整体的吸收特征,盐碱土的光谱曲线总体上较平缓,但是反射率数值不同,说明不同实验高度下土样的光谱反射强度不同。在350~2 500 nm间特征吸收带的出现位置也不尽相同。整体趋势为在350~1 500 nm区间内平缓上升,部分高度存在小部分波段区间波动;1 500~1 800 nm间增速较缓,1 800~1 950 nm以及2 450~2 500 nm区间内受室外测量的大气中水汽影响发生剧烈上下波动。 将3 cm、4 cm、5 cm、6 cm、7 cm等5个实验高度下土壤样本的原始光谱反射率按在不同高度下与土壤样本的EC值进行逐波段的相关性分析,结合图2以及考虑到室外实验的开放特性,容易受到空气中水汽的影响,因此在进行相关分析时去除波段1 350~1 400 nm、1 810~1 950 nm、2 450~2 500 nm这3个受水汽影响较大的波段。计算350~2 500 mn间波段与土壤盐分的相关系数,用于选取建模敏感波段(图3)。从图3可以看出,不同实验高度下所获取的土壤原始光谱反射率在350~2 500 nm间呈现正相关关系。不同实验高度下的波段趋势较为一致,以实验高度5 cm和7 cm表现较好。不同实验高度下的光谱反射率与盐分的相关性在350~550 nm间呈现良好相关性。在350~1 000 nm间相关系数波动下降,在区间1 000~1 810 nm内波动缓慢,较为平滑。区间1 950~2 450 nm对盐分反映较为敏感,存在连续的上下波动态势,相关系数数值也较好。 图3 不同实验高度下土壤原始光谱反射率与EC值的关系Fig.3 Correlation coefficients between soil original reflectance and EC values at different experimental heights 将3 cm、4 cm、5 cm、6 cm、7 cm等5个实验高度下土壤样本的反射率的一阶和二阶微分变换结果,按在不同高度下与土壤样本的EC值进行350~2 500 nm间波段的相关性分析(图4)。从图4可以看出,5个实验高度下经过微分数学变换后的光谱数据与土壤EC值的相关性明显增强,表现为相关系数在0附近快速震荡,并呈现明显的正负相关区域,表明经过微分变换放大了原始光谱中的隐晦信息,提升了相关性,并且在不同的实验高度下的反射率二阶微分变换优于一阶微分。综合分析5个实验高度下一阶微分和二阶微分变换后的相关系数绝对值来分析,实验高度5 cm表现最好,通过显著性检验的特征波段数量最多,与土壤EC值相关系数高,集中体现在波段400~420 nm、1 020~1 100 nm、1 200~1 340 nm等这3个区间内,其中波段1 672 nm处的一阶微分相关系数达到0.702,波段853 nm处的二阶微分相关系数达到了0.711。此外,实验高度7 cm的反射率二阶微分变换后的706 nm、1 709 nm等波段的相关系数数值超过0.662,实验高度3 cm的反射率二阶微分变换后的562 nm、2044 nm等波段的相关系数数值均超过0.553,实验高度4 cm与6 cm较其他实验高度表现较差,且经过显著性检验的波段数量少于其他实验高度。实验高度6 cm的二阶微分变换后的波段709 nm、874 nm等波段出相关系数数值超过0.506,实验高度4 cm的一阶微分变换后的波段752 nm、789 nm处相关系数数值超过0.429。 图4 不同实验高度下一阶、二阶微分光谱数据与EC的相关系数Fig.4 The correlation coefficients of the second and second-order differential data with EC at different experimental heights 由图3和图4分析得到,不同的实验高度下原始光谱反射率与经过一阶微分、二阶微分数学变换后的光谱反射率与土壤的EC值的相关系数,光谱反射率经过一阶微分和二阶微分的数学转换后,与盐分的相关系数绝对值有明显提升,按照紫(350~455 nm)、蓝(455~492 nm)、绿(492~577 nm)、黄(577~597 nm)、橙(597~622 nm)、红(622~780 nm)、近红外短波(780~1 100 nm)、近红外长波(1 100~2 500 nm)的划分[27],在这8个波段范围(除去受水汽影响的噪音部分波段)内,对应不同测量高度分别选择原始反射率以及不同微分形式下的反射率变换结果与盐分相关系数绝对值最大的4个波段作为土壤盐分敏感波段,并且均通过1%水平验证,将其确定为建模波段,结果如表2所示。 表2 不同实验高度下的敏感波段(波长nm)Table 2 Sensitive bands(wavelength) at different experimental heights 据表2所得出的相关分析结果,在56个样本中随机选取36个作为建模集,建立土壤EC值与反射率及其一阶微分、二阶微分的逐步多元线性回归方程,不同测量高度下多元线性回归模型建模结果如表3示。 表3 多元线性回归方程模型分析统计表Table 3 Statistics of three-element linear regression equation model analysis 据表2所得出的相关分析结果,在56个样本中随机选取36个作为建模集,建立土壤EC值与反射率及其一阶微分、二阶微分的偏最小二乘线性回归方程,不同测量高度下偏最小二乘模型建模结果如表4所示。 从表3和表4可以看出,不同实验高度的光谱数据对样本含盐量的响应差异较大。原始光谱反射率在两种模型计算后对盐分的拟合精度较差,估算能力不高,不同高度下两种模型中指标R2范围在0.48~0.74之间,RPD值范围为1.13~2.37,经过数学微分变换后,5个实验高度下反射率一阶微分、二阶微分建立的两种模型精度均有所上升,且二阶微分变换优于一阶微分。此外,不同实验高度的3种光谱形式在两种模型中的表现差异也较大,整体上偏最小二乘回归模型在对盐分的精度与拟合上优于多元线性回归模型。综合5个实验高度下3种不同光谱形式在两种模型中的结果,实验高度5 cm为最佳高度,其反射率二阶微分在偏最小二乘回归模型中R2=0.91、RMSE=0.40、RPD=3.08;其次为实验高度7 cm,反射率二阶微分在偏最小二乘回归模型中R2=0.80、RMSE=0.95、RPD=2.41。第三为实验高度3 cm,反射率二阶微分在偏最小二乘回归模型中R2=0.76、RMSE=1.10、RPD=2.30。另外两个实验高度4 cm与实验高度6 cm表现较差,所得全部实验结果中R2较小、RPD数值小于2,模型精度低且模型不稳定,针对盐分进行估算的精度不高。 选取5 cm测量高度作为最佳光谱测量高度,利用20个验证样本分别对其一阶和二阶微分变换的多元线性回归模型和偏最小二乘回归模型进行验证(图5)。 表4 偏最小二乘回归方程模型分析统计表Table 4 Statistics of partial least squares regression equation model analysis 图5 土壤含盐量的多元线性模型与偏最小二乘模型预测结果检验(n=20)Fig.5 Test of prediction results of multivariate linear model and partial least squares model of soil salinity(n=20) 从图5显示的结果可以看出反射率二阶微分变换优于一阶微分,且偏最小二乘回归模型的预测精度高于多元线性回归模型的精度。此外,从两种模型预测比较来看,多元线性回归模型中预测值与实测值中存在异常值,异常值存在与含盐量的较高的区域,偏离对角线附近;而偏最小二乘模型的预测值与实测值的表现整体较好,聚集在对角线附近,说明其稳定性和预测精度均优于多元线性回归模型。而异常值出现的另一个原因可能也是由于本文所用的多元线性模型与偏最小二乘模型只是运用了全波段中筛选后的敏感波段加入模型进行计算,容易造成局部有效信息的丢失,但是选取敏感波段进行计算有精简计算模型、计算量小的优势,可以用于盐分信息的快速估测。 原始的光谱数据包含的数据量巨大,与土样EC值进行相关分析后相关系数较低,因此,将原始光谱数据进行微分处理,可以放大光谱中的隐晦信息,提高土壤含盐量模型的预测精度。同时,结合其他实验高度数据分析表明二阶微分变换后的光谱数据更能有效的提升与土样EC值的相关系数,是本文最佳的光谱变换形式,这与杨爱霞等和李志等的研究结果相同[28-30]。 对土壤EC值的多元线性回归方程与偏最小二乘方程的建模结果与预测效果进行检验,通过比较模型指标R2、RMSE、RPD的大小,表明偏最小二乘回归模型的稳定性与预测能力优于多元线性回归,模型研究结果与前人的研究结果较为一致[31-32]。这是由于多元线性回归模型在建立过程中会出现多种共线性的问题,导致结果的不稳定性,影响了估算精度,而偏最小二乘回归模型是建立在传统的回归方法上,同时引入了方差分析和主成分分析,是一种多变量回归方法,因此在对土样EC值的估算中表现更好[33]。而本文仅考虑多元线性回归方程与偏最小二乘方程这两种线性模型进行实验,后续研究中应该采用多种非线性模型进行计算来对比分析,以寻求更好更适合的反演模型。 不同的实验高度在估算土壤盐分中差异存在且无明显规律性,实验高度5 cm表现最佳,其次为实验高度7 cm和实验高度3 cm,而实验高度4 cm和实验高度6 cm的光谱数据在经过数学变换后在两种模型中精度上升较小,RPD范围在1.13~1.82之间,预测精度不高。综上考虑,不同的实验高度针对盐分的估算表现不同,这种现象出现的原因可能是由于实验为室外实验,实验调控中外在环境的不可控性以及大气中的水汽影响仍然存在;同时,土样经过烘干研磨后碱土表面颜色深浅不一,这也可能直接影响了光谱反射率大小,从而影响光谱信息对盐分指标的拟合精度;此外,盛用土样的铝盒面积较小,且土样表面的颗粒度的差异也会影响光谱数据的测量结果,这也可能导致不同高度下回归模型精度和预测结果的差异性。同时,本文在设计实验高度上结合实验用铝盒面积选取为3 cm~7 cm,这一实验高度间隔为1 cm,在后续研究中,可以进一步调整测量高度范围和测量间隔,进一步提高预测模型的精度和适用范围。 本研究使用松嫩平原典型盐碱土地区土壤样本,通过室外光谱实测实验调控不同实验高度,定量研究不同实验高度对土壤盐分反演精度的的影响,对样本的光谱反射率进行一阶微分与二阶微分的数学变换结果可以有效提高与土壤电导率间的相关性,通过在多元线性回归方程与偏最小二乘回归方程中进行盐分的估算结果表明实验的高度中表现最好的为5 cm,反射率二阶微分变换后在偏最小二乘回归方程中R2=0.91,RPD=3.08,模型稳定,预测精度较高,可以用于对盐碱化土壤含盐量进行估算。不同实验高度的建模结果对盐分的估算结果存在差异,但规律性不明显,表现优良程度从高到低为5 cm、7 cm、3 cm、6 cm、4 cm,说明室外实验中实验高度的不同对于光谱数据影响较大,且偏最小二乘模型建模结果优于多元线性回归模型。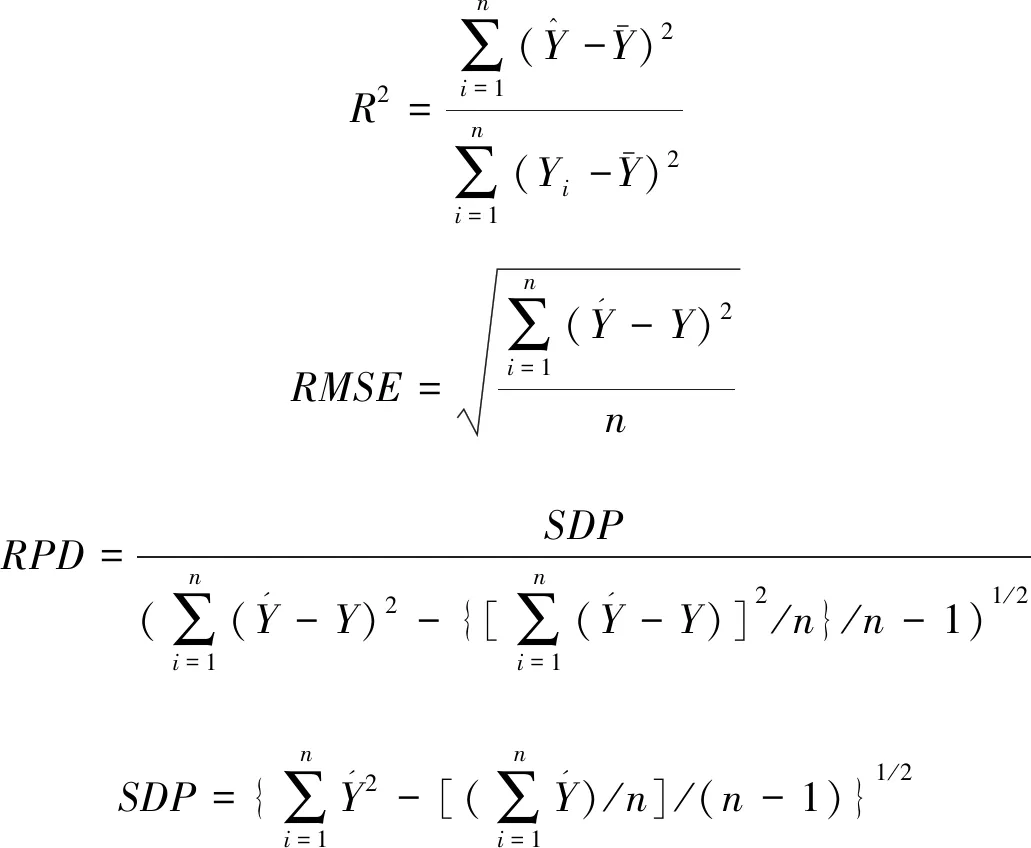
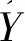
2 结果与分析
2.1 相关分析

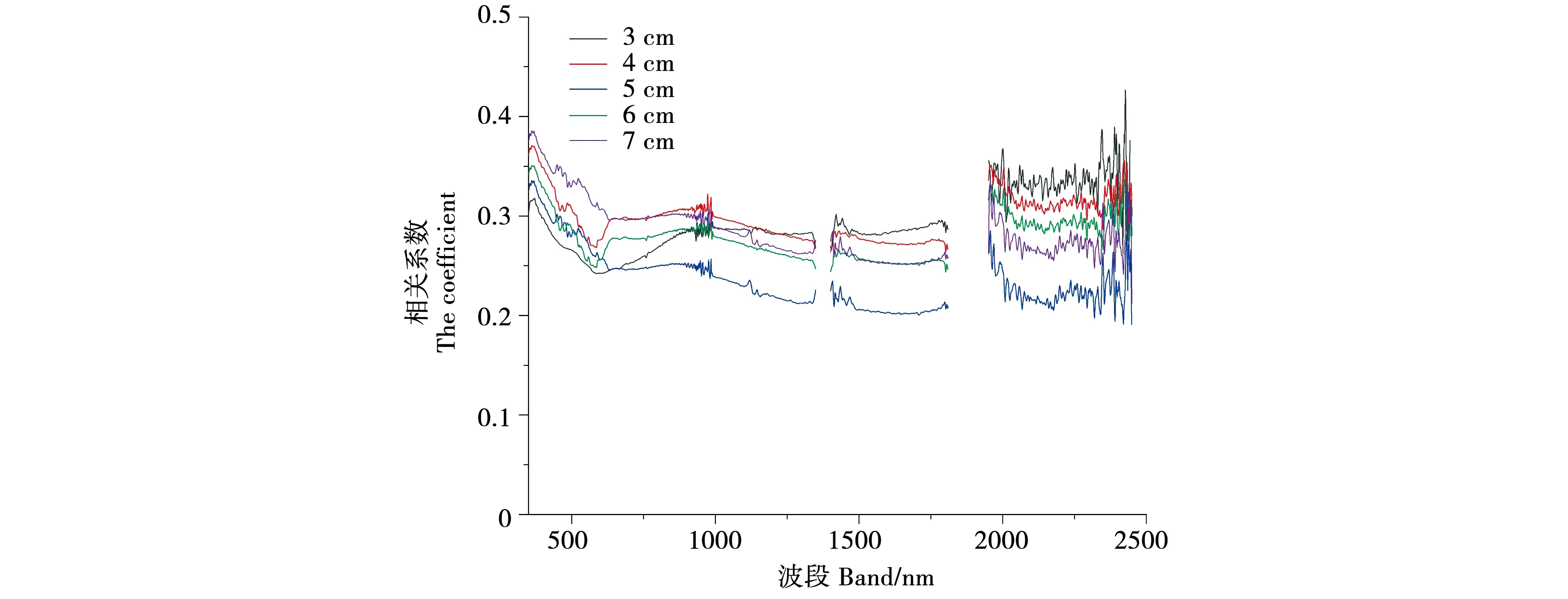
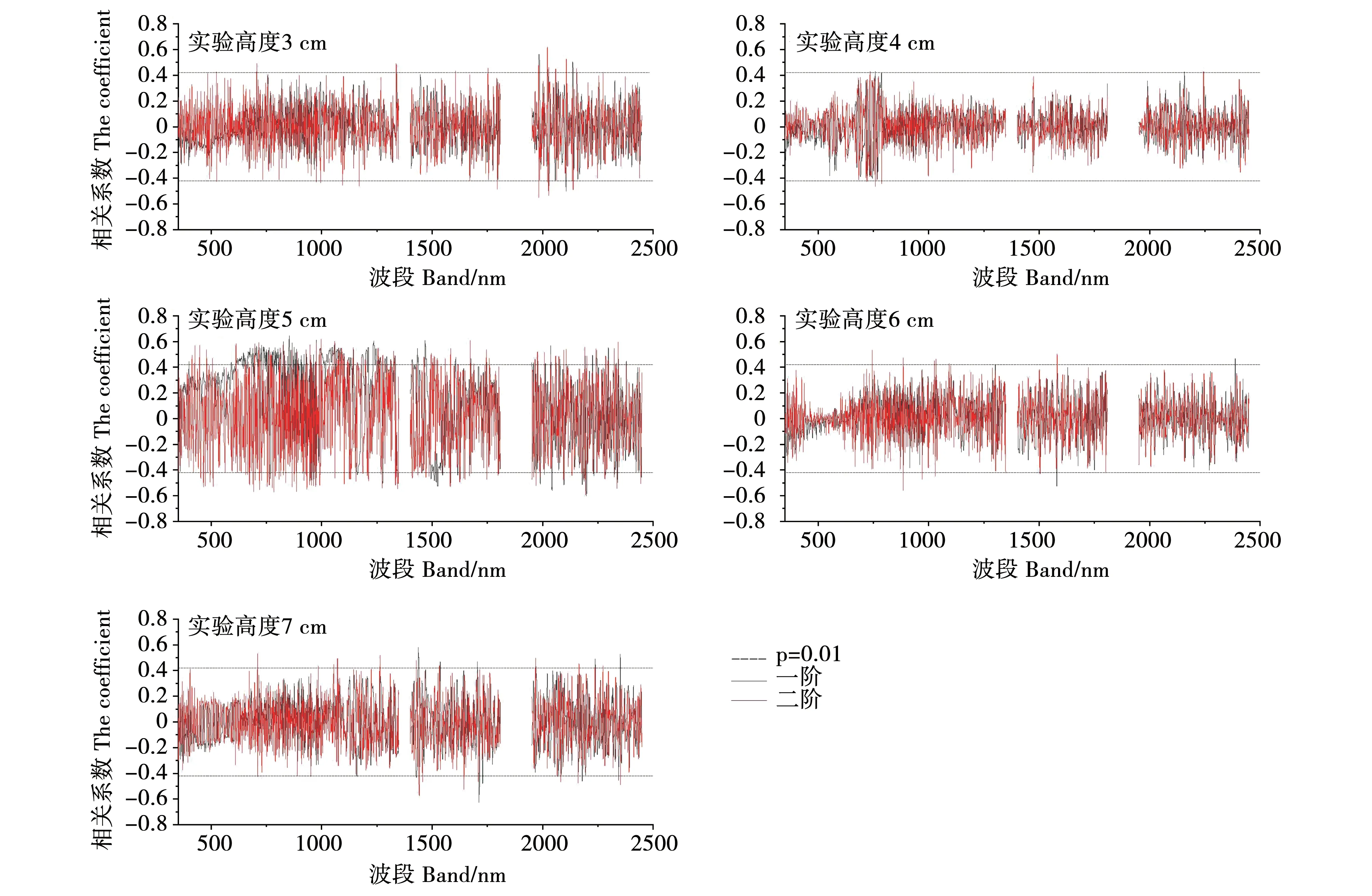
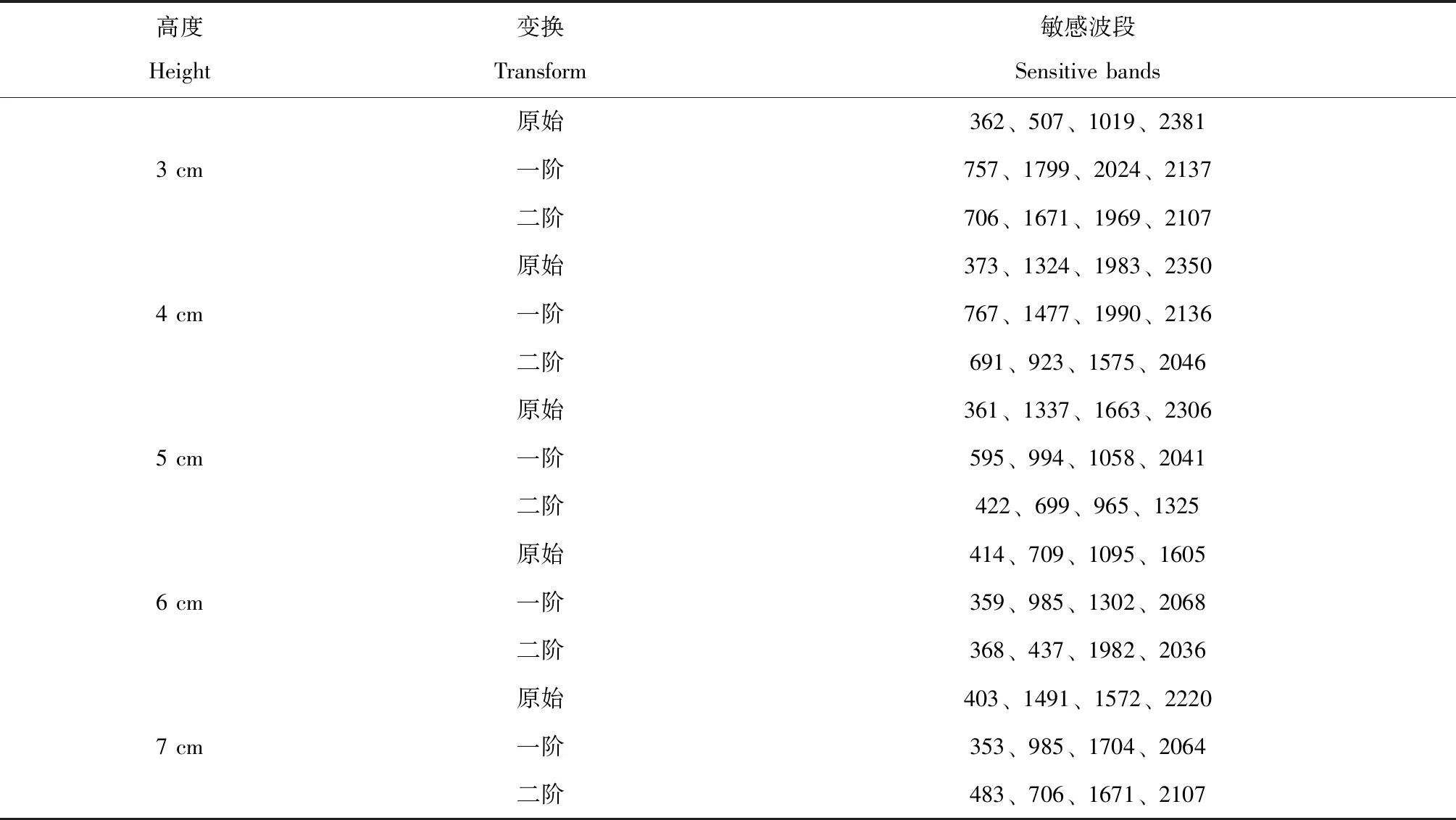
2.2 土壤盐分的光谱模型
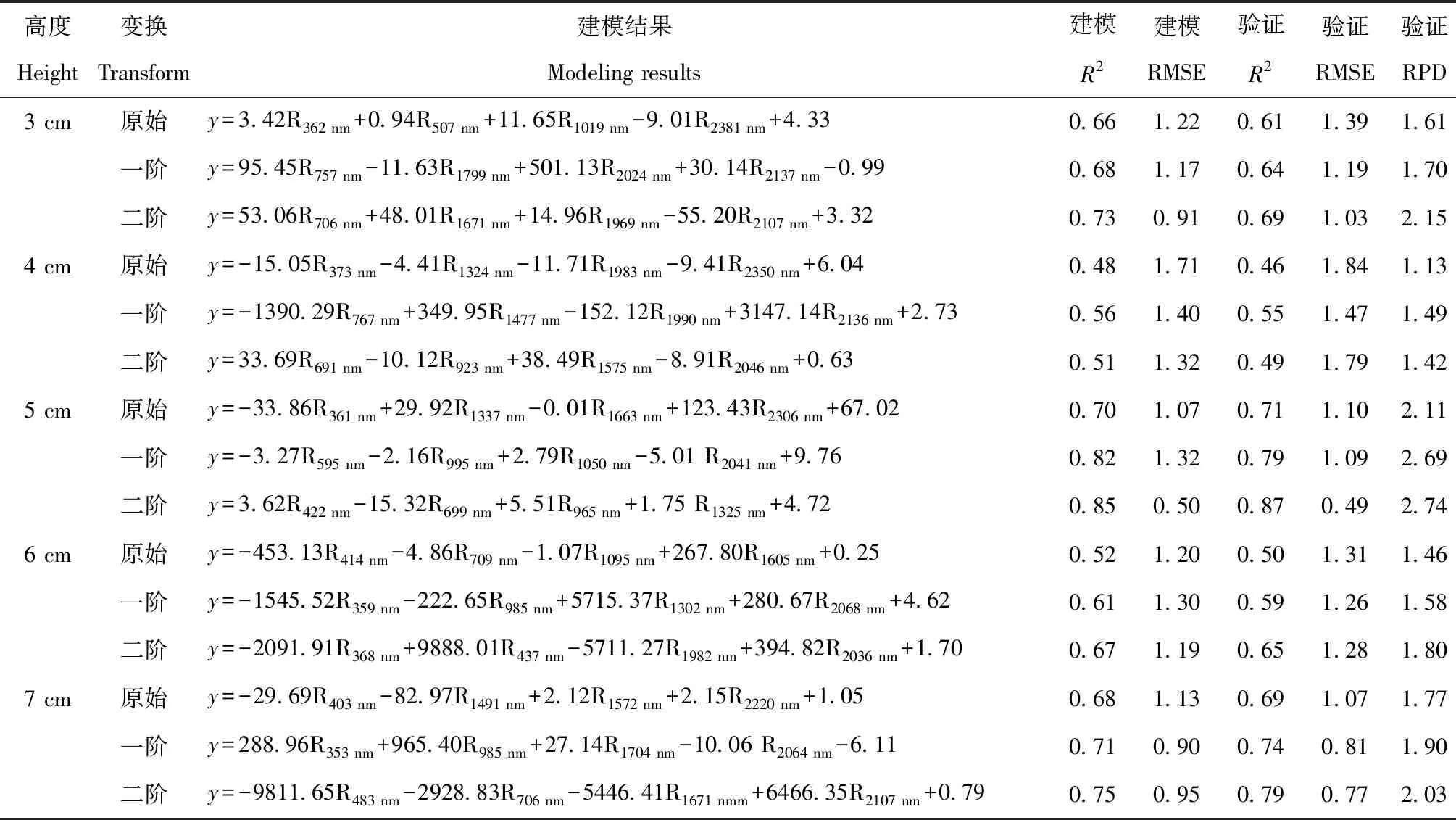
3 讨 论
4 结 论
