二维单程波有限差分法叠前时间偏移技术应用
2020-12-10何鑫
何 鑫
(中国石化勘探分公司勘探研究院,四川成都610041)
偏移技术是地震数据处理的三大基本技术之一[1-3]。 在确定反射界面真正空间位置时,最好用最常用的就是偏移处理。 早期的地震偏移技术是手工操作的制图技术, 只能确定反射点的空间位置,对地震波的波动特性无法反映, 效率低且精度不高。上世纪70年代后,随着计算机技术的发展,地震数字处理也获得了空前的发展,偏移结果能够同时反映地震波的运动学和动力学特征,反映的地下构造细节更加丰富,促进了油气勘探技术的进步。
早期的计算机运算能力有限,偏移处理技术是叠后偏移,输入的是水平叠加结果,即先叠加后偏移,应用条件为地下构造简单、倾角不太大的情况。当地下构造复杂,倾角较大,不满足自激自收的假设条件时,就需要用到叠前偏移。 叠前偏移是先偏移后叠加,理论上不存在倾角限制,更符合复杂构造的成像需要。 叠前偏移有叠前时间偏移和叠前深度偏移,叠前深度偏移相比叠前时间偏移,多考虑了地震波在两个速度界面传播时的偏折, 在横向速度变化剧烈的地区成像精度更高, 难点是复杂构造速度建模, 而且运算效率比叠前时间偏移低。 在横向速度变化不大时,叠前时间偏移精度就基本可以满足勘探需要了, 且对速度的精度要求没有叠前深度偏移高,运算速度更快,在地下构造倾角较大但横向速度变化不大的地区有较大的优势[4-9]。
描述地震波在地下传播情况的是波动方程,偏移技术的数学本质是在一定边界条件和初始条件约束下求解波动方程的数值解。 求解波动方程有微分解和积分解两大类。 20世纪70年代, 美国的Claerbout教授首先利用有限差分求解单程波波动方程近似式[2],得到第一张数字处理偏移剖面,此后,Schneider发展了利用波动方程积分解的Kirchhoff积分偏移技术[10]。 Kirchhoff积分偏移技术由于适应观测系统能力强,运算效率高,在叠前时间偏移里居主流地位,诸多叠前时间偏移技术应用的文献也主要是Kirchhoff积分偏移技术[11-20],有限差分叠前时间偏移较少。Kirchhoff积分偏移通过射线追踪,把接收点的波场反推到地下反射点,通过积分求和获得偏移结果,计算效率高,该方法对观测系统特性要求较低,所以适用性广,但射线追踪天然存在多值性,焦散是其缺陷,偏移结果保幅性稍差。 差分法通过差分逼近微分的方法进行波场延拓,把地表接收的波场反推到地下反射点,不需要射线追踪,克服了焦散问题,保幅性更好。 该方法对观测系统的规则性要求较高。 差分法由于使用离散的方法,存在数值频散的隐患,需要选择合适的步长把数值频散控制到可接受的程度。
1 基本原理
地震勘探中我们通过观测,得到地面的地震波波场,为了得到地下结构图像,需要将地表波场向下外推,利用一定的成像条件,获得地下反射界面的正确位置,这个过程就是偏移。 数学上主要通过求解波动方程边值问题来实现,二维声波波动方程表示如下:
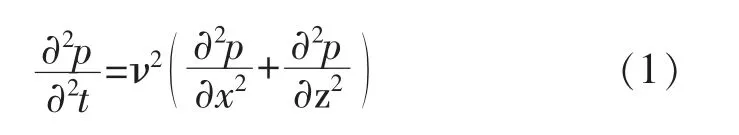
混合条件表示为:

式中,p(x,z,t)是待求地下地震波场,ν是地下介质速度,m/s,φ (x,t) 是地表接收的波场。 在式(2)约束下求解式(1)条件不充分,需要补充以下条件:

但实际地震勘探中,式(3)中的φ(x,t)是地表接收波场关于z的一阶导数, 实际中是无法观测的,有限差分法求解式(1)时为避免式(3)的限制,需要对式(1)中的z降阶。 主要办法是上、下行波分解。
分别对式(1)中x,z,t进行傅里叶变换,可得:

式中,ω为圆频率,kx,kz分别是x,z方向的波数。(4)式中取正号描述下行波,取负号描述上行波。 对(4)式取负号并对z取傅里叶反变换可得二维上行波方程:

求解(5)式时,马在田提出通过对根式进行连续分式展开[1],根据近似式的不同,得到适应不同角度的波动方程近似式。 令ω,(5)式根号内容连续分式可表示:
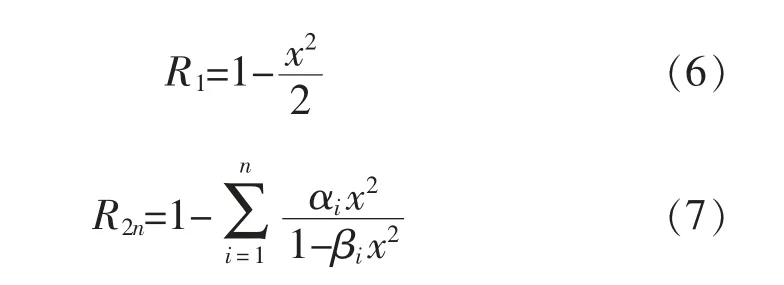
(6)式代入式(5)时反变换回x-t域就是Claerbout15°上行波方程。 Lee 和Sub(1985)[1]求出了式(7)某个特定的倾角和最佳参数组合(αi,βi),一直求到第十阶(表1)。

表1 最优化分式单程波动方程的参数(Lee 和Suh,1985)[1]
时间偏移与深度偏移的本质区别是偏移所用的速度场,式(3)中的是均方根速度νrms(t)时,求解(3)式就是时间偏移,式(3)中的ν是深度-速度ν(x,z)时,求解(3)式就是深度偏移。
波动方程成像原理主要有三种[10]:①爆炸反射面成像原理;②测线下延成像原理;③时间一致性原理。
爆炸反射面成像原理由D.Leowenthal 首先提出[10]。 该原理把地下反射界面上每一个点看成爆炸源,假设在t=0时刻,反射界面上所有的爆炸源同时起爆,上行反射波到达地面的观测点,波的传播速度为ν'=ν/2。 实际记录的地震波包括了上行波又包含下行波,但爆炸反射面原理仅考虑上行波,所以传播时间减半,速度为地震波真实速度。 将地面测得的波场利用波动方程式做反时间方向传播,即向下延拓,则t=0时的波场值就正确的描述了地下反射界面的位置,从而实现偏移成像。 该成像条件适用于叠后偏移。
测线下延成像原理也叫沉降观测原理,在双平方根方程叠前偏移过程中, 只对上行波场进行延拓,相当于向地下同时延拓震源与接收点,当二者重合时(零偏移距),零时间的波场值就作为该空间点的成像值。
时间一致性原理是:反射界面总是存在于下行波的到达(或产生)与上行波的产生(或到达)同一时刻的地方。 同时向下延拓震源和接收波场,二者时间相同的地方认为是反射点。
当φ(x,t)为叠加剖面时,应用爆炸反射面原理得到的偏移结果就是叠后偏移剖面,当φ(x,t)为叠前记录,常用CMP域道集,应用测线下延成像原理得到偏移结果就是叠前偏移剖面。
总之,当(3)式中ν是均方根速度νrms(t),φ(x,t)为二维CMP域道集,应用有限差分法求解(3)式,并应用测线下延成像原理取成像值,就是本文的二维单程波波动方程叠前时间偏移技术。
2 应用
本文的实际地震数据来自南方某区块,勘探目标区地表出露地层为二叠系的碳酸盐岩, 在风化、溶蚀等作用下,溶洞、裂缝发育,整体表现为喀斯特地貌,地表岩石弹性差,导致能量衰减严重,地震波传播路径和地震波场复杂, 原生和次生干扰严重,影响地震信号接收质量。 激发和接收条件的不利导致地震勘探资料信噪比低, 采集到的地震信号较弱,要求在处理上更加注意弱信号成像,因此选择了理论上保幅性更好的有限差分法进行试验。
有限差分叠前时间偏移要求采用偏移距规则的数据。 采集时是二维直线观测,观测系统规则性较好,处理时再借助偏移距规则化处理技术,能够满足有限差分法对资料偏移距规则的要求。 本次处理在Echos系统上完成。
影响偏移结果质量的因素包括:偏移前数据质量,包括静校正、信噪比、偏移距规则化等;偏移速度;偏移方法。 偏移前数据质量是基础,需要做好静校正、去噪等基础工作。 偏移速度是关键,本文尝试了在DMO速度基础上优化初始偏移速度场。 偏移方法是核心,本文尝试了不同于常规的克希霍夫积分法的有限差分法。
(1)偏移前数据质量保证。 综合运用多种保幅去噪手段,多域压制各种噪声,提高叠前资料信噪比。 在低信噪比资料处理中,静校正的重要性尤显重要,除了层析静校正,采用了具有全局寻优特点的模拟退火剩余静校正技术,很好地解决了山地低信噪比的静校正问题。 图1是初始叠加(图1a)与最终叠加(图1b)的对比,可以看出综合运用多种保幅去噪与静校正手段后,地震资料的信噪比有了很大改进,叠加同相性改善明显,波组特征清晰。 为叠前偏移奠定了良好的数据基础。

图1 叠加效果
(2)偏移速度场建立。 克希霍夫积分法运算效率高, 其CRP道集具有指示偏移速度场是否合适的能力:CRP道集下弯则偏移速度偏高,CRP道集拉平则偏移速度合适,CRP道集上翘则偏移速度偏小,适合作为偏移速度场建立的工具。 叠加速度场平滑作偏移初始速度场只适合水平地层,南方山地资料多数不具备这个条件。 DMO是一种部分偏移技术,具有一定校正叠加速度倾角效应的能力,DMO速度作为偏移初始速度场相比叠加速度更有优势, 但在DMO速度基础上作一定范围的扫描,通过道集拉平程度选择合适的初始偏移速度效果更好。 图2是不同初始偏移速度场计算出来的同一个CMP位置的CRP道集,叠加速度(图2a)对应的道集下弯最严重,说明是严重偏高的,DMO速度(图2b)对应的道集下弯程度有所改善,但下弯依然明显,说明DMO速度作初始偏移速度场依然偏高。 在DMO速度基础上通过百分比扫描方式优化初始偏移速度场(图2c),道集基本拉平,此时初始偏移速度场是合适的。 在此基础上进行剩余速度优化, 得到最终的偏移速度场。

图2 不同初始偏移速度场对应的CRP道集
(3)偏移方法。 本文比较了主流的克希霍夫积分法叠前时间偏移和有限差分法叠前时间偏移在同一个偏移速度场下的结果。 积分法存在多路径、高频近似的缺陷,有限差分法是波场延拓,不存在射线路径问题,保幅性更好。 如图3所示,在深层有限差分法(图3b)波组特征稳定性更好,弱信号成像自然。 而克希霍夫积分法(图3a)波组稳定性较差,弱信号成像蚯蚓化,保真度低。 断背斜边界是断裂带,信噪比低;克希霍夫积分法偏移画弧严重,差分法偏移画弧轻, 反映在剖面上就是差分法更加自然,如图3a所示。

图3 不同叠前时间偏移方法深层结果对比
图4是浅层的对比,克希霍夫积分法(图4a)浅层成像较差,受到偏移画弧干扰明显;而有限差分法(图4b)的波组特征明显好于克希霍夫积分法,偏移画弧干扰不明显,反射层能追踪。 图3、图4显示的剖面均位于测线中部。

图4 不同叠前时间偏移方法浅层结果对比
该区部署的X井钻探的是页岩气勘探目的层志留系龙马溪组,是一套海相泥页岩,页岩气钻探一般是通过水平井,对井轨迹的精度要求很高,相比常规直井勘探,对地震剖面的质量要求更高。 图5是X井设计井轨迹叠合在克希霍夫叠前时间偏移剖面,图6是X井设计井轨迹叠合在有限差分叠前时间偏移剖面上,总的趋势上,两种方法的结果差异不大,同相轴和井轨迹都较吻合,区别在于水平井段(红色箭头)起始端的同相轴成像质量,有限差分法的成像略有优势。 图6应用有限差分叠前时间偏移结果的改进使得圈闭解释的面积比图5克希霍夫叠前时间偏移的结果略有扩大,实钻也证实井轨迹水平段起始就是稳定的优质泥页岩, 按照图5的解释容易误认为水平段起始位置地层破碎,不利于水平井钻进。
在喀斯特地质形态等地区,由于地表复杂造成地震信号较弱的地区,有限差分叠前时间偏移相比克希霍夫偏移具有更好的保幅性和弱信号成像能力,构造位置成像与克希霍夫偏移相当,因而有限差分叠前时间偏移既适合构造油气藏的勘探,也适合岩性油气藏的勘探,值得尝试。

图5 X井设计井轨迹—克希霍夫PSTM剖面

图6 X井设计井轨迹—有限差分PSTM剖面
3 结论
(1)地表为喀斯特地貌的地震勘探区,存在着地震信号信噪比低的问题, 需要在处理中考虑保幅、弱信号成像的问题。 克希霍夫积分法叠前时间偏移是目前地震数据处理主流的叠前时间偏移方法,其运算效率高、适应观测系统能力强。 但由于需要射线追踪,存在射线多路径问题,成像聚焦性差。有限差分法通过差分近似微分, 延拓地震波场成像,避免了射线追踪,地震保幅性更好,在喀斯特地区地震资料处理中更有优势。
(2)通过实际资料对比,在喀斯特地型地震信号信噪比低的地区,有限差分法计算的效果相比克希霍夫积分法无论是浅层还是深层,在波组特征稳定性、 保幅性和弱信号成像等方面都有明显优势,值得推广。 当然,任何偏移都需要做好偏移前数据处理和合适的偏移初始速度场的建立。
