地震作用下空间网格结构倒塌模式分析

2020-12-09吴冲戴君武彭卿吴碧野成维根

地震研究 2020年3期

吴冲戴君武彭卿吴碧野成维根

摘要：以显式动力分析方法为基础，模拟了强震作用下3种跨度网格结构的倒塌全过程，通过数值分析发现：水平地震作用下网格的倒塌形式以强度破坏为主，竖向地震作用下以动力失稳破坏为主，三向地震作用下为水平与竖向地震作用倒塌形式的耦合。对比分析了3种跨度网格结构倒塌形式和倒塌时地震波幅值，结果表明：平板网格结构倒塌形式与跨度关系不大，但易倒塌程度与跨度直接相关。得到了网格结构的倒塌形式和倒塌时构件首先失效的位置，可为实际工程结构的倒塌预防与控制提供一定的参考。

关键词：地震作用;倒塌模式;数值模拟;空间网格结构

0 引言

空间网格结构诞生于20世纪初，是一种新颖的大跨空间结构体系，具有平面布置灵活、空间造型美、自重轻等诸多优点，现已被大量应用于大型体育建筑、公共建筑、工业建筑中（董石麟，姚谏，1994;张毅刚等，2005）。这些建筑中一般会有大量人群活动，一旦出现质量缺陷或遭遇非预期荷载而导致结构倒塌，将会造成巨大的生命和财产损失。近年来，大跨度空间结构连续性倒塌事件屡有发生（黄兴淮等，2012;高亮，2012）。

结构连续性倒塌分析可以分为2种类型：连续性倒塌风险评估和连续性倒塌仿真（胡晓斌，钱家茹，2006）。多年来国内外学者对钢筋混凝土结构、钢框架、空间钢结构连续性倒塌分析做了很多研究（王亚勇，2017;高峰等，2009;胡学仁等，1995;曹正罡等，2008;沈世钊，支旭东，2005;Semenyuk，Zhukova，2006），形成了统一的设计思想和相应的设计规范（建筑抗震设计规范，GB 50011—2010;空间网格结构技术规程，JGJ7—2010;钢结构设计标准，GB 50017—2017），但这些研究主要集中于连续性倒塌风险评估，而对连续性倒塌全过程的仿真还比较缺乏。对于“跨度是否是影响倒塌形式的关键因素”“结构发生倒塌时构件首先失效的位置在哪里”等问题，现有研究還没有给出明确具体的结论。

为了深入了解在强震作用下空间网格结构的全过程倒塌形式，探究跨度是否是影响倒塌形式的因素和发生连续性倒塌时首先失效构件的位置，就需要对在地震作用下结构从破坏直至倒塌整个过程中的塑性状态进行全面而深入的分析。因此，本文对在强震作用下3种不同跨度的网格结构的倒塌形式进行仿真，深入分析了在地震作用下构件首先失效的位置以及不同跨度对网格的倒塌形式的影响。

1 分析案例概况

本文分析案例的抗震设防烈度为Ⅷ度，设计基本地震加速度为0.2 g，场地类别为Ⅲ类，地震分组为一组，特征周期为0.45 s。设定10 m×10 m，20 m×20 m，30 m×30 m的3种跨度的正方四角锥钢管球节点双层平板网格进行研究;3种空间网格结构均采用3D3S软件进行两阶段设计，即上部平板网格依据现行钢结构设计标准设计，下部竖向支承柱子依据混凝土结构设计规范设计。3种空间网格结构的顶层高分别设为6，6.2和6.5 m，下层平面尺寸分别为9 m×9 m，18 m×18 m，28.5 m×28.5 m;下弦杆竖向支承柱高5 m，直径分别为300，500和700 mm的混凝土圆柱，所有杆件材性为Q235B钢材。

2 有限元模型参数设置

有限元模型的参数设置是数值模拟过程中重要的内容，参数设置的合理与否直接关系到数值模拟结果的可信度。

2.1 有限元分析软件的选取与模型验证

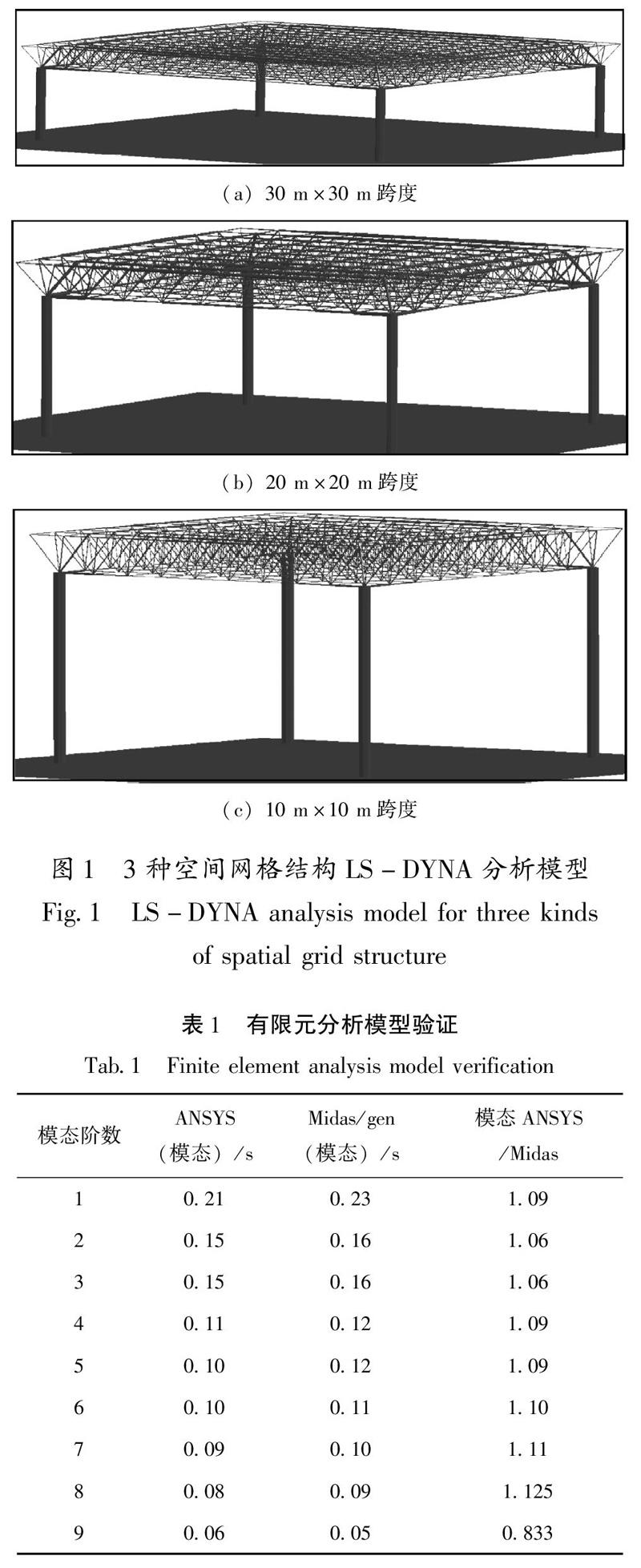
本文采用ANSYS/LS-DYNA软件进行分析，该软件以中心差分法为基础，能够很好地处理各种非线性收敛问题（张凯，2017）;同时，综合了ANSYS的前处理与LS-DYNA强大的非线性分析功能，可以得到在强震作用下结构完整的动力响应以及损伤失效过程，是一种较为精确的分析方法。3种空间网格结构的分析模型如图1所示。

在对空间网格结构进行有限元分析时，杆件单元的选择通常有2种方式：杆单元和梁单元（两端约束释放）。虽然梁单元的地震组合、荷载组合系数与杆单元有区别，但本文仍选择了梁单元进行分析，原因如下：①本文是模拟在强震作用下结构的倒塌形式以及失效机理，因为杆件相对较长，产生的弯矩相对较小，其节点刚度对整体结构倒塌模式影响不大;②笔者参考了黄兴淮等（2012）进行的空间网格结构的倒塌模式分析研究及其杆件单元的选取，该研究指出在分析空间网格结构倒塌时，使用杆单元与梁单元得出的倒塌模式相差不大，可以使用梁单元代替。综上，本文采用简化处理，网格结构下弦杆竖向支承柱和上部平板网格杆件采用BEAM161梁单元模拟;地面采用SHELL163梁单元模拟，且定义为刚体。

由于节点与弦杆、腹杆之间采用螺栓球的方式连接，螺栓球节点本身具有一定的质量，为了考虑这部分增加的质量，通常在设计过程中通过增大1.2倍的重力加速度来简化考虑，本文采用同样的简化方式。通过数值模拟结果发现，进一步细化网格虽能提高精度，但会消耗巨大的计算时间，还可能出现意外中断的情况（黄兴淮等，2012），因此本文空间网格结构的弦杆和腹杆在有限元的网格划上均为1份，柱子为5份。在数值模拟之前应进行结构模态分析及模型验证，其结构的频率如表1所示。由于涉及3种跨度结构模型，本文仅验证其30 m×30 m跨度的网格结构，通过2种软件（Midas/gen，ANSYS）计算对比得出，结构周期相差很小，证明此ANSYS有限元模型合理。

2.2 材料模型选取

在强震作用下结构构件会发生断裂甚至结构整体会发生倒塌，此时材料进入塑性阶段。为使模拟结果更加准确，则需定义合理的材料参数。由于数值模拟过程中涉及到钢材的弹塑性本构关系，参考陆新征和江见鲸（2001）利用LS-DYNA程序模拟的世贸中心遭受恐怖袭击造成的连续性倒塌，并借鉴林红等（2016）进行的结构倒塌的数值模拟，本文材料模型选取考虑失效的Plastic Kinematic（塑性随动模型）的材料模型。

在数值模拟过程中若某单元材料应变值达到限值时，LS-DYNA程序自主认定该单元失效，将该单元在原有结构中删除，在之后的计算过程中忽略该单元的影响。因此单元材料失效应变的限值设定十分重要，目前还不存在统一结论。本文失效应变值参考刘成清和何斌（2014）的研究结果，见表2。

2.3 材料的应变率效应

在地震作用下应考虑材料的塑性应力强化和高应变率对材料屈服应力的影响，Cowper-Symonds（与应变率相关的参数模型）模型可以考虑应变速率对材料屈服应力的影响。材料屈服应力表示为：

式中：σ0为初始屈服应力;ε为应变率;C和P为应变率参数;β为硬化参数;εeffP为有效塑性应变;EP为塑性硬化模量，由下式给出：

式中：E为材料的弹性模量;Etan为切线模量。

定义该模型时需要输入包含弹性模量、密度、泊松比、屈服强度、切线模量、硬化参数以及应变率参数，本文参数的选取参考张凯（2017）的研究结果，见表2。

2.4 接触类型与阻尼参数设置

本文采用LS-DYNA软件提供的Contact Automatic Single Surface（自动单面接触）模拟上部结构之间和上部结构与刚性地面之间的碰撞。质量加权和刚度加权阻尼在显示动力分析中是阻止非真实震荡的有效方法。本文摩擦参数设置依据金焕和戴君武（2013）进行的结构抗震分析参数选取;阻尼参数设置参照周颖等（2012）进行的钢框格架振动台试验参数的设置，见表2。

2.5 结构承受恒、活荷载组合

本文依据吴莉莉（2017）提出的荷载组合原则，在结构分析时采用1倍恒荷载和0.25倍活荷载组合，不考虑侧向力，比如风、雪载组合等，其荷载组合为：

式中：W为结构所承受的恒、活荷载组合;WD为结构恒荷载;WL为活荷载。恒载取0.5 kN/mm2，活荷载取0.6 kN/mm2。由于结构发生倒塌时，结构上满布活荷载的可能性较小，故荷载组合中只考虑了0.25倍的活荷载作用，且施加荷载时使用EDLOAD命令对节点进行施加。

2.6 地震动施加方式

为了更加合理地模拟地震作用，本文将地震动加速度记录以动力荷载的形式作用于地面，计算得到模型上层的位移变形以及损伤演化过程，分析在地震荷载作用下结构的倒塌破坏过程。本文数值模拟采用的地震动记录为美国1940年加州El Centro地震波，其地震波时程曲线及频谱曲线如图2所示。

3 双向水平地震作用下的倒塌模拟

根据规范规程要求结构抗震设计时应考虑双向水平地震作用，即施加X，Y两个方向的地震动。

3.1 30 m×30 m网格结构

本文输入地面加速度峰值（PGA）时，按0.1 g的增量从小到大依次试算，选取使结构发生倒塌的最小地震强度。通过试算，当PGA=3.5 g时，结构刚好发生倒塌。图3给出了典型时刻倒塌过程模拟结果。结果表明：0～10.76 s，结构基本完好;10.76 s时，支座附近下弦杆突然达到失效应变限值并从整个结构中消失;10.76～11.62 s，随着持续的地震作用，与失效构件相连的腹杆、弦杆持续达到失效应变;当达到11.62 s时，支座附近腹杆开始失效;11.62～11.98 s，随着失效构件数量的增加，结构发生了很大的变形，结构中原来力的传递路径被改变，结构重力无法由剩余的杆件支撑并传递到柱上;11.98 s时，在重力作用下结构发生倒塌。由于在水平地震作用下，柱子附近的下弦杆首先达到失效，在整个破坏过程中没有杆件屈曲，因此该破坏类型定义为在强震下结构的动力强度破坏（沈世钊，支旭东，2005）。

3.2 20 m×20 m网格结构

在进行20 m×20 m网格结构倒塌形式模拟时，通过试算，发现当PGA=4.0 g时，该网格结构刚好发生倒塌。图4表明：0～10.08 s，结构完好;到10.08 s时，支座附近下弦杆突然破坏;10.08～10.96 s，与失效构件相连的腹杆、下弦杆达到失效应变;到10.96 s时，与支座连接的下弦杆、腹杆开始失效;10.96～11.54 s，随着失效构件数量的增加，结构中原来受力的传递路径被改变，结构重力无法由剩余的杆件支撑并传递到柱上;11.54 s时，在重力作用下结构发生倒塌。

3.3 10 m×10 m网格结构

在进行10 m×10 m網格结构倒塌形式模拟时，通过试算，当PGA=6.0 g时，该网格结构刚好发生倒塌，结构随时程倒塌分布形式如图5所示。倒塌过程及形式与3.1，3.2节两例类似，不再赘述。

从图3～5可以看出：10 m×10 m，20 m×20 m，30 m×30 m网格结构倒塌时间分别为6.58，11.54和11.98 s;倒塌时PGA分别为6.0，4.0和3.5 g;可见跨度越大抗倒塌能力越弱。3种跨度网格结构的双向水平地震波幅值（PGA）远大于Ⅷ度（0.2 g）地区罕遇地震进行的弹塑性时程分析时得出的PGA=0.4 g，说明本文按规范设计的3种网格结构在双向水平地震作用下是非常保守安全的。综上得出：双向水平地震作用下网格结构倒塌模式与跨度关系不大，但易倒塌程度与跨度直接相关;在双向水平地震作用下3种网格结构首先破坏的杆件位置均发生在支座附近的下弦杆。

4 竖向地震作用下的倒塌模拟

为了研究结构的竖向倒塌规律以及倒塌模式，需要施加竖向地震动即沿Z向施加地震动。

4.1 30 m×30 m网格结构

模拟在构竖向地震作用下30 m×30 m网格结倒塌形式模拟时，通过试算发现当垂直于地面的PGA=2.5 g时，该网格结构刚好发生倒塌。由图6可见：0～7.02 s，在竖向地震作用下，结构跨中上弦杆发生弹性屈曲，当上弦杆弹性屈曲后，结构进行内力重分布，随着地震作用的增加，整体结构初现V字形，此时结构上弦杆受压，下弦杆受拉;到7.02 s时，跨中的下弦杆首先达到失效应变;7.02～7.96 s时，与失效构件相连的下弦杆、腹杆不断失效;7.96 s，与支座相连接的上弦杆、腹杆出现失效;7.96～8.2 s时，结构中原有力的传递路径被明显改变，结构整体出现明显的凹陷，即整体呈现明显V字形;8.2 s时，结构重力无法有效地传递到柱子上，在重力作用下结构发生倒塌。该类型破坏存在典型的失稳屈曲，所以该类型破坏为动力失稳破坏（沈世钊，支旭东，2005）。

4.2 20 m×20 m网格结构

模拟在竖向地震作用下20×20 m网格结构倒塌形式模拟时，通过试算，发现当垂直于地面的PGA=3.0 g时，该网格结构刚好发生倒塌。由图7可见：0～6.92 s，跨中上弦杆进入屈曲阶段;6.92s，跨中的下弦杆首先达到失效应变;6.92～9.22 s，与失效构件相连的下弦杆、腹杆不断失效;9.22 s时，与支座相连的上弦杆、腹杆出现失效;9.22～13.02 s，结构中原有力的传递路径被改变，结构整体呈现明显的凹陷;13.02 s时，结构重力无法有效地传递到柱子上，在重力作用下该结构发生倒塌。

4.3 10 m×10 m网格结构

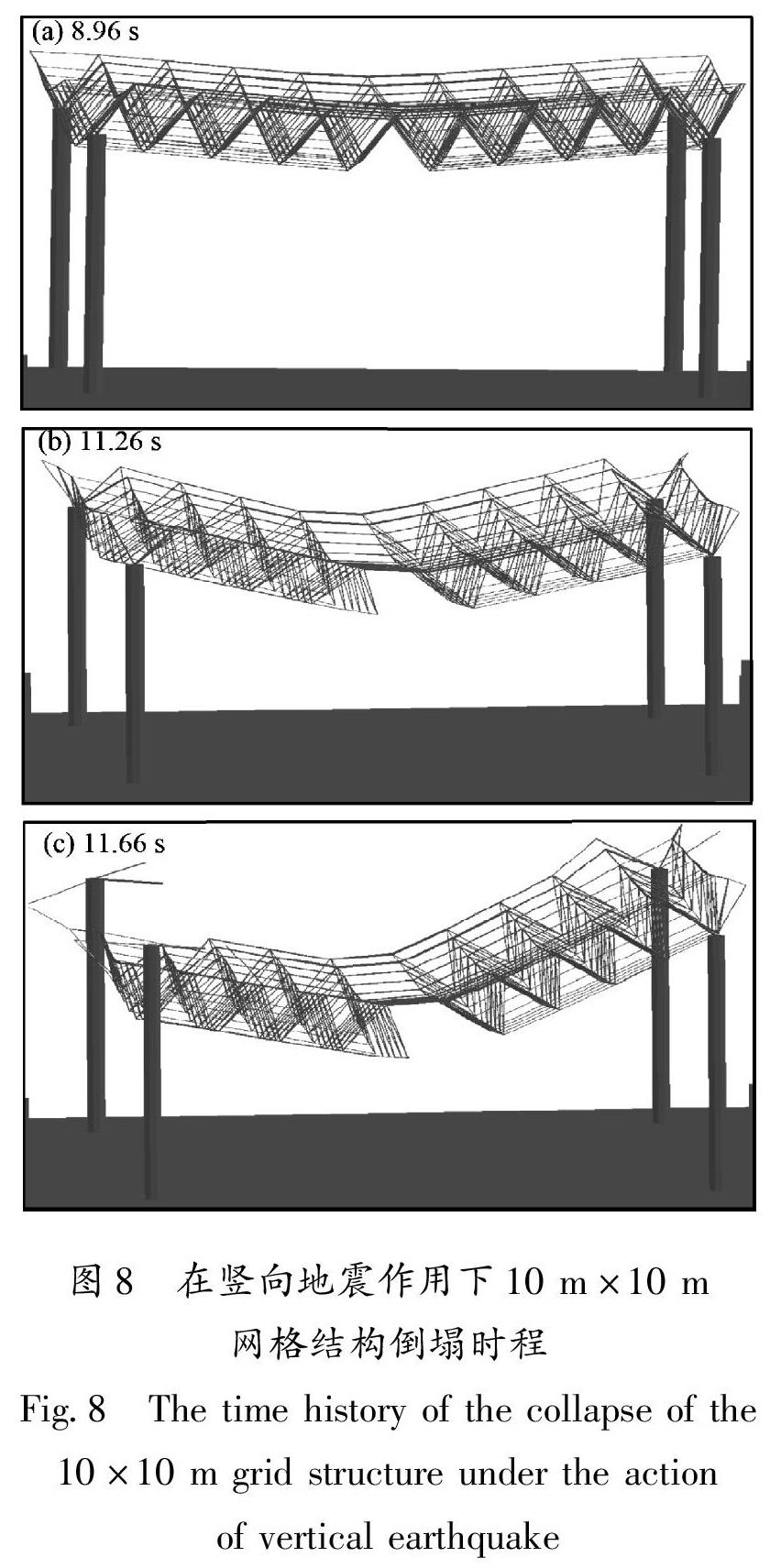
模拟在竖向地震作用下10×10 m网格结构倒塌形式模拟时，经试算，发现当垂直于地面的PGA=5.0 g时，结构刚好发生倒塌。图8给出结构随时程倒塌分布形式，其倒塌过程及形式与图6，7类似，不再赘述。

从图6～8得出：10 m×10 m，20 m×20 m，30 m×30 m网格结构倒塌时间分别为11.66，13.02和8.2 s;倒塌时输入的地震波幅值为5.0，3.0和2.5 g。

3种跨度的网格结构竖向地震波幅值（PGA）远大于Ⅷ度（0.2 g）地区罕遇地震进行的弹塑性时程分析得出的 PGA=0.4 g，说明在竖向地震作用下按规范设计的网格结构也有很大的安全裕量。由此得出：竖向地震作用下结构的倒塌模式与跨度关系不大，但易倒塌程度与跨度直接相关;在竖向地震作用下3种网格结构首先破坏的杆件位置均发生在结构跨中的下弦杆。

对竖向地震作用的分析表明：网格跨度越大其抗倒塌能力越弱;相同跨度的网格结构，发生倒塌时的竖向与双向地震PGA值对比表明：竖向抗倒塌能力弱于双向，即竖向地震作用对该类网格结构的倒塌起控制作用。

4.4 竖向倒塌模式与试验模型以及实际灾害现象对比 Mwakali（1990）对一个双层平板网格结构进行了竖向加载试验，实验中结构整体呈现明显的凹陷，即整体呈现V字形，如图9a所示。本文通过LS-DYNA得到的3种网格结构在竖向地震作用下的倒塌模式与试验结果表现一致。

1998年某地区由于遭受雪灾造成一批轻型网格结构发生倒塌（黄兴淮，2015），结构倒塌后呈现明显的V字形，其倒塌后结构形式如图9b所示，说明通过本文数值模拟计算得出的倒塌模式与实际灾害现象表现比较吻合。

5 三向地震作用下的倒塌模拟

由于篇幅限制，以及3种倒塌模式的相似性，所以本节只列举其中30 m×30 m跨度的网格结构来进行分析。

通过试算，发现水平双向、竖向和三向PGA=1.6 g时，该网格结构刚好发生倒塌。由图10可见：三向地震作用下，0～7.16 s，结构基本完好，到7.16 s时，跨中的下弦杆达到失效应变;7.16～7.86 s，与失效构件相连的下弦杆和腹杆不断失效;7.86 s时，与支座相连接的上弦杆、腹杆出现失效;7.86～8.18 s，结构中力的传递路径被改变，结构整体呈现明显的凹陷;8.18 s时，网格重力无法由剩余构件有效的传递到柱子上，在重力作用下结构发生倒塌。

通过分析可知，三向地震作用下30×30 m跨度网格结构倒塌时对应的PGA幅值远小于双向、竖向地震，表明网格结构设计中应取三向地震作用同时输入进行分析。显然，即使是在三向地震作用下，30 m×30 m网格结构倒塌时对应的PGA幅值也远大于设防烈度Ⅷ度、设计基本地震加速度值为0.2 g地区大震弹塑性时程分析所采用的罕遇地震的PGA=0.4 g。

6 结论

通过对3种不同跨度网格结构进行多维地震作用下倒塌数值模拟分析，得到如下主要结论：

（1）当仅受水平地震作用时，网格结构的倒塌模式偏于动力强度破坏，其首先破坏杆件位置发生在支座附近的下弦杆。当仅受竖向地震作用时，网格结构的倒塌模式偏于动力失稳破坏，其首先破坏杆件位置发生在结构跨中的下弦杆;倒塌前网格结构整体呈现V型凹陷。当受三向地震作用时，网格结构的倒塌形式既包含动力强度破坏又包含动力失稳破坏。

（2）将本文3种网格结构发生倒塌的PGA与按规范设防烈度8度、设计基本地震速度值为0.2 g地区大震弹塑性时程分析所采用的罕遇地震的PGA=0.4 g 对比可见，本文的结果均更大，说明在地震作用下3种网格结构均偏于安全保守。

（3）从不同跨度网格结构倒塌形式对比得出，网格倒塌形式与跨度关系不大，但易倒塌程度与跨度直接相关。加强在地震作用下网格结构首先破坏的杆件，可以提高其抗连续倒塌能力。

参考文献：

曹正罡，范峰，沈世钊.2008.大矢跨比单层球面网壳弹塑性稳定性研究[J].哈尔滨工业大学学报，40（2）：183-186.

董石麟，姚谏.1994.网壳结构的未来与展望[J].空间结构，1（1）：3-10.

高峰，楊大彬，靳卫恒.2009.K6型单层网壳极限承载力对杆件失效的灵敏度分析[J].工程建设与设计，（8）：16-19.

高亮.2012.双层柱面网壳结构抗倒塌能力的分析[D].太原：太原理工大学.

胡晓斌，钱家茹.2006.结构连续倒塌分析与设计方法综述[J].建筑结构，36（S1）：573-577.

胡学仁，罗永峰，凌冰.1995.穹顶网壳的优化形体和试验分析[J].空间结构，1（1）：29-37.

黄兴淮，徐赵东，杨明飞.2012.多维地震下大跨网格结构倒塌分析与抗倒塌措施[J].东南大学学报（自然科学版），42（1）：109-113.

黄兴淮.2015.大跨网格结构倒塌模式与多维隔减震控制研究[D].南京：东南大学.

金焕，戴君武.2013，外廊式RC框格结构教学楼的抗震性能研究[J].土木工程学报，46（5）：71-77