四阶椭圆型方程组主次特征值之比的下界
2020-12-09黄振明
湖南城市学院学报(自然科学版) 2020年6期
黄振明
(苏州市职业大学 数理部,江苏 苏州 215104)
微分算子特征值的研究是几何分析中的一个重要课题.有学者曾说过,有振动的地方就有特征值和特征向量,在不同的情形下,特征值具有相应的物理含义,常表示为物体振动的频率、物体受力变形的临界压力或微观粒子在不同运动状态时的能级等.同样的,广义特征值也具有很强的实际意义.例如,经典的Buckling 问题[1]就是一类广义特征值问题,即

其中,Δ2是 Rm上的双调和算子;ν 是有界区域Ω边界∂Ω 的单位外法向量.问题(1)描述了夹持薄板在受到外部压力后变弯曲的临界负荷,在工程和建筑力学等方面有着重要的意义.因此,广义 特征值问题越来越受到国内外学者们的重视.数十年来,人们在此领域取得了一些研究成果[1-7],但迄今为止,鲜有学者对问题(1)所描述的方程组进行过讨论.笔者尝试将其进行推广,讨论如下四阶椭圆型方程组的广义特征值问题:

其中, i = 1,2, … ,l ,l 为大于或等于1 的整数;Ω ⊂ Rm( m≥2); X= ( x1, x2, …, xm);常数 aij=aji(i, j = 1,2, … , l ).
1 准备知识

2 引理
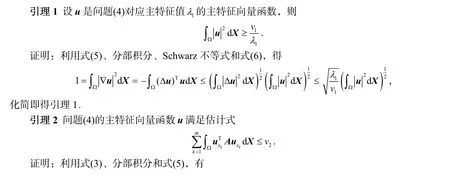


3 主要结果

4 一般情形


