不规则形超材料电磁隐身斗篷的设计研究
2020-12-09刘冶李竹影夏江敏
◆刘冶 李竹影 夏江敏
(海军工程大学湖北 430033)
超材料作为21世纪初逐渐兴起的新型人工材料,由于具备一系列自然界材料所不具备的超常物理性质,从问世起十多年来,关于超材料的研究一直是国际上的研究热点。2006年Pendry教授团队在《Science》杂志上发表文章,论述基于坐标变换理论设计的超材料能够实现对电磁波传播的控制[1]。随着世界上第一个二维简化参数的超材料电磁隐身斗篷的问世[2],越来越多的科学家们开始对超材料隐身器件及超材料新型装置展开了广泛而深入的研究,并取得了很多开创性的成果[3-10]。在前人研究的理论基础上,本文基于坐标变换理论,对不规则形超材料电磁隐身斗篷进行电磁参数设计并及进行数值仿真验证,使隐身斗篷在构型得到了拓展。
1 不规则形超材料电磁隐身斗篷的电磁参数推导
这里所提及的不规则形,指的是仅用一个极坐标方程就能够表示的曲线。由于极坐标方程可以用来表示各种不同形状的封闭曲线,相比于圆柱形、椭圆柱形、正多面体形等具有规则形状的斗篷,横截面为不规则形状的柱状理想斗篷(以下简称“不规则形斗篷”)的研究更具有一般性。这一类斗篷的空间变换示意图如图1所示。
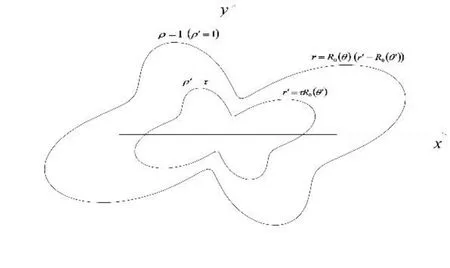
图1 不规则形超材料电磁隐身斗篷的横截面空间变换示意图
在图1中,原空间由极坐标方程为r=R0(θ)所表示的曲线围成的封闭空间,变换空间由极坐标方程分别为r′=R0(θ′)与r′=τR0(θ′)所夹的环域空间。图中,设ρ为矢径归一化系数,定义为
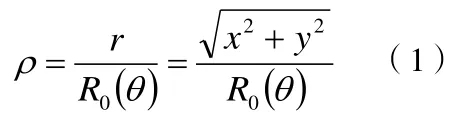
从(1)式可以得到直角坐标系下的坐标分量为
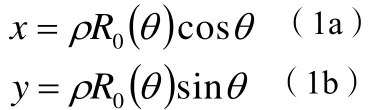
从(1)式可以看到,取ρ=1(ρ′=1)时将得到不规则形斗篷的外轮廓曲线,取ρ′=τ时将得到不规则形斗篷的内轮廓曲线,当ρ取0到1之间的数值时,会得到与斗篷外轮廓线(或内轮廓线)共形的一系列封闭曲线,因此从ρ(ρ′)的定义可以对不规则形斗篷空间变换的过程进行阐述:原空间(ρ,θ,z)中 0 <ρ<1的柱形区域压缩为变换空间(ρ′,θ′,z′)中τ<ρ′<1的环状柱形区域。上述的空间变换的表达式为ρ′=(1-τ)ρ+τ。
此时变换空间中的直角坐标分量为
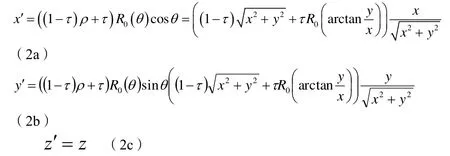
此时,空间变换的雅可比矩阵的行列式为
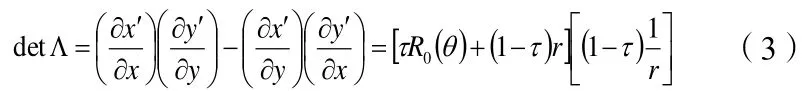
根据坐标变换理论[3],可推导得出该斗篷的电磁参数张量的分量为:
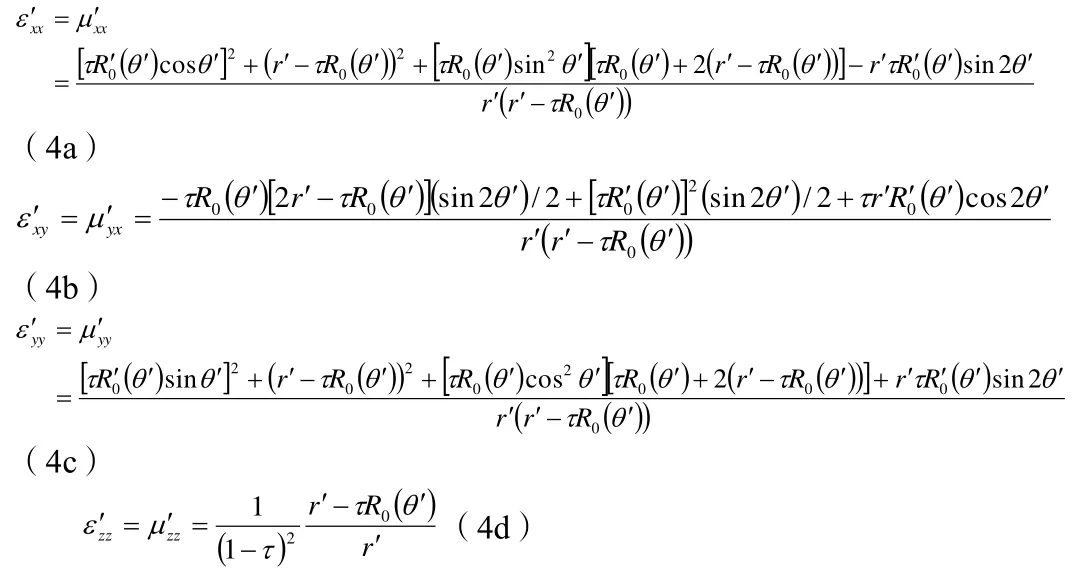
2 数值仿真验证
根据(4)式,采用Comsol Multiphysics商用仿真软件,对不规则形斗篷进行数值仿真验证。波源选取工作频率为8.5GHz的平面TM波,四周为吸收边界,求解域为 0 .46m× 0.36m的矩形区域,TM波是从求解域的左端进行垂直入射。在斗篷模型的设计上,设计了内外轮廓线共形的不规则形斗篷,其中:外轮廓线的极坐标方程为
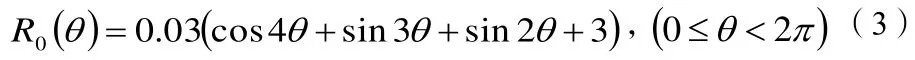
压缩系数τ=0.5。对于TM波,将(5)式中的设置为不规则斗篷的电磁参数张量的分量,即可完成仿真中对斗篷材料参数的设计。最终得到的仿真计算结果如图1所示。
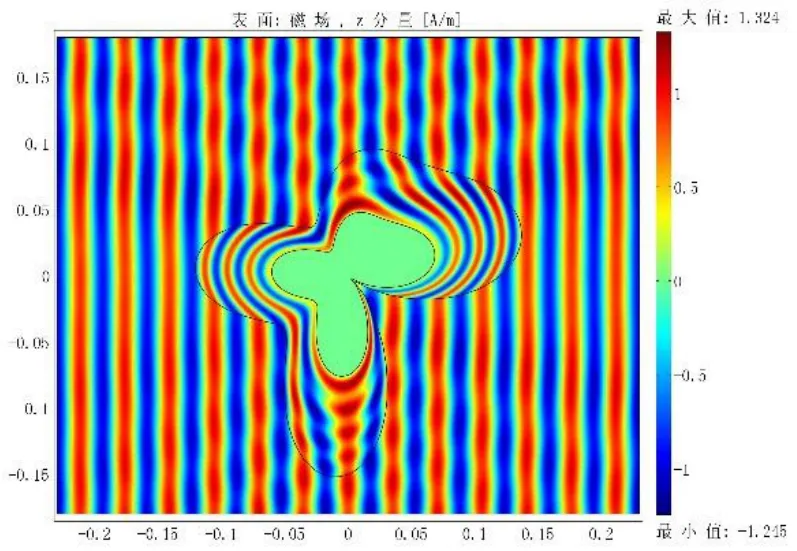
图2 不规则形超材料隐身斗篷的磁场分布
图2显示了不规则形斗篷的磁场分布,验证了该斗篷电磁参数张量表达式的正确性。从图中求解域的磁场分布情况来看,TM波从外部自由空间进入斗篷区域后,等相位面基本上是沿着斗篷内边界曲线的形状进行弯折的;当TM波从斗篷区域透射至外部自由空间时,透射波的等相位面又恢复至初始的形状。从外部自由空间的磁场分布来看,空间中不规则形斗篷的存在并没有对TM波在自由空间中的传播产生影响。从整个求解域的磁场分布可以看到,TM波在求解域空间传播的过程中,并没有发生散射,反射和波被吸收等现象,再一次地验证了不规则形斗篷具有理想的电磁隐身性能
3 结论
应用坐标变换理论,本文设计出不规则形超材料电磁隐身斗篷,并采用有限元仿真软件对斗篷的电磁特性进行数值仿真,结果显示所设计的斗篷实现了电磁隐身功能,从而验证了该装置电磁参数张量推导的正确性,该研究成果对于超材料电磁隐身斗篷形状设计的拓展有一定的促进作用。
