图形翻折中的“勾股定理”

文 季黎明

与基本图形相关的图形的翻折变换历来都是中考热门，其中直角三角形占有一席之地。与直角三角形息息相关的是勾股定理，它揭示了直角三角形三边之间的数量关系，是解决问题的有力工具。当直角三角形“遇上”翻折变换，会发生什么呢？下面，通过一道中考改编题，我们一起来看看勾股定理是如何帮我们解决问题的。

例（2017·江苏无锡改编）如图1，在四边形ABCD中，已知：∠DAB=∠B=∠C=∠D=90°，AB=CD=10，BC=AD=6，若点P为射线BC上的一点，将△ABP沿直线AP翻折至△AEP的位置，使点B落在点E处。当△PEC为直角三角形时，求PB的长。

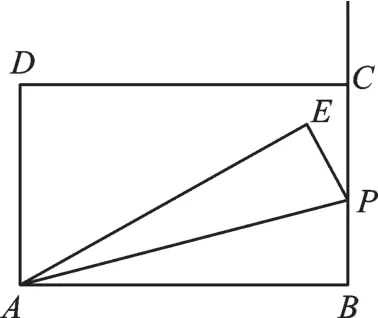
图1

【分析】首先，由“P为射线BC上的一点”，我们将点P按“在线段BC上”和“在线段BC的延长线上”这两种位置关系进行讨论。

其次，“△PEC为直角三角形”。哪个角是直角呢？题中并未指明。所以，我们围绕直角同样要展开讨论。

接下来，如何进一步解决问题呢？以“当点P落在线段BC上且∠PEC=90°时”这一情况为例，此时点E刚好落在对角线AC上（如图2）。借助翻折，自然地可以得到AB=AE，EP=PB。我们的目标是线段PB的长度。线段PB满足PB+PC=6，即EP+PC=6，而线段EP、PC恰好构成了Rt△PEC的直角边与斜边。另一条直角边EC又是可求的。所以，在Rt△PEC中由勾股定理可以得到PE2+EC2=PC2。利用线段EP、PC的和为定值，可以设EP=x，则PC=6-x，将其代入PE2+EC2=PC2，建立关于x的方程。把握好这个方法后，我们可以“以不变应万变”。

【略解】（1）当点P落在线段BC上时：

①当∠PEC=90°时（如图2），设PB=x，由翻折可得△ABP≌△AEP，所以AB=AE=10，EP=PB=x，则PC=6-x。

在Rt△ABC中（对于数值的化简，同学们在以后的二次根式中会学）。

因为AE=10，所以EC=2 34-10。

在Rt△PEC中，PE2+EC2=PC2，解得x=。

图2

图3

②当∠PCE=90°时（如图3），点E刚好落在线段CD上，不难得出CE=2。

在Rt△PEC中，同样以PC2+EC2=PE2为等量关系列方程，解得。

③当∠EPC=90°时，这种翻折情形并不存在，舍去。

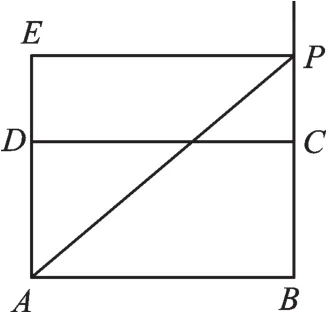
图4

图5

（2）当点P落在线段BC的延长线上时：

①当∠EPC=90°时（如图4），点E刚好落在AD的延长线上。

此时，四边形ABPE是正方形，所以PB=AB=10。

②当∠PCE=90°时（如图5），点E落在CD的延长线上。

由翻折得AB=AE=10，设EP=PB=x且PC=x-6，易得CE=18。

在Rt△PEC中，结合勾股定理列方程解得PE=PB=30。

③当∠PEC=90°时，这种翻折情形并不存在，舍去。

综上，△PEC为直角三角形时，PB=或30。

【小结】本题是一道常见的翻折变换问题，回首上述4种情形，每一次翻折变换均可以得到三角形全等。利用全等得到线段之间的数量关系并以此设未知数，表示出相关线段，我们不难发现：翻折中出现的Rt△PEC的三边要么可求，要么可用未知数表示，于是，在Rt△PEC中用勾股定理建立方程，求解未知数。本题还可以这样设计，已知E点到四边形某边的距离，考查P点的位置。2017年无锡市的中考数学第28题的最后一问正是这样的问题。同学们试试自己设计并解决，相信你一定行！