说说“高”的“那些事”

文 任 蕾

提起“高”，同学们一定会想到直角三角形，想到勾股定理。下面，我们的话题就从一道关于“高”的习题说起：

习题在△ABC中BC边上的高AD=6，求边BC的长。

【错解】如图 1，画△ABC，并过点A作AD⊥BC，垂足为D。在Rt△ABD中，BD=同理，在 Rt△ACD中，CD=，所以BC=BD+CD=8+2=10。

【分析】运用勾股定理求线段长是常见方法，上述按照“常规”思路得出的答案有错吗？有。错在何处？本题没有图形，所以要将“文字语言”转化成“图形语言”。在实际操作中多数同学会画出图1，即三角形的高AD在三角形内部，殊不知BC边上的高的位置并不确定，AD还可能在三角形外部。

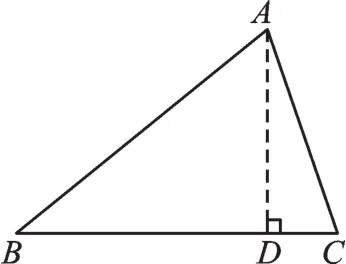
图1

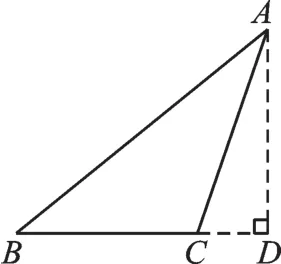
图2

【正解】除了上述情况，当AD在△ABC外部时（如图2），过点A作AD⊥BC交BC的延长线于点D。这里求得BC=BD-CD=6。所以BC边长为10或6。

【点评】关于“高”的问题常用勾股定理解决。三角形的高可能在三角形内部，也可能在三角形外部，甚至在三角形的边上。我们在解题时要根据三角形的形状进行分析，若无法确定三角形形状，要进行分类讨论。

拓展已知等腰△ABC中，AB=AC=5，△ABC的面积为10，求边BC的长。

【解析】由三角形面积可以联想到三角形的高，但是高的具体位置还要根据三角形的形状进行讨论。

若△ABC为锐角三角形（如图3），BC=2 5；若△ABC为钝角三角形（如图4），BC=4 5。同学们可以尝试写出具体解答过程。

图3

图4

【归纳】通过以上例题，我们不难看出，运用勾股定理求有关三角形的高的问题时，往往需要分类讨论，这样才能全面地分析问题的本质。因为“三角形的高在形内或形外”是不能一概而论的，我们应考虑有多个解的可能性。

分类讨论是一种基本而又重要的数学思想方法，也是考试的热点之一。掌握了这个思想，可使我们的数学思维更加灵活、缜密，更有条理。