勾股定理——“数”与“形”的纽带

文 徐松兵

数学家华罗庚说过，数缺形时少直观，形少数时难入微。我们本章学习的勾股定理就真正做到了“数”与“形”的完美结合，下面让我们一起来感受一下。

一、以形解数

例1在数轴上确定表示的对应点。

【解析】众所周知，数轴上的点除了可以表示有理数，也可以表示无理数。如何在数轴上确定表示的点呢？我们在学习勾股定理时，利用勾股定理可以作出长为、等的线段，依次做下去，总可以作出长为的线段（如图1）。除此之外，我们还可以联想到数的拆分：5=1+4或者5=9-4（同学们可以思考一下：为什么找1、4、9），即可以考虑在直角三角形中直接构造长为的边。

方法1如图1，在点A处作AB⊥OA，且AB=1，则OB=；作CB⊥OB，且CB=1，则OC=；作DC⊥OC，且DC=1，则OD=2；作DE⊥OD，且DE=1，则OE=。以点O为圆心，OE的长为半径作弧，交数轴于点M，则点M所对应的数为 5。

图1

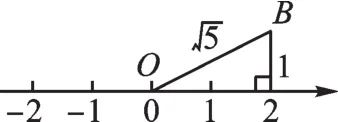
图2

图3

方法2如图2，考虑直接构造直角边长分别为1和2的直角三角形，则斜边长为。

方法3如图3，构造斜边长为3、直角边长为2的直角三角形，则另一条直角边长为。

【归纳】“以形助数”，将数量关系和几何图形巧妙结合，使复杂问题简单化，抽象问题具体化，有助于把握数学问题的本质，发现问题中隐含的意义。

二、以数解形

例2如图4，AB为一棵大树，在树上距离地面10m的点D处有两只猴子，它们同时发现地面上的C点处有一筐水果。一只猴子从D处向上爬到树顶A处，利用挂在A处的滑绳AC滑到C处，另一只猴子从D处滑到地面B，再由B跑到C。已知两只猴子的路程都是15m，求树高AB。

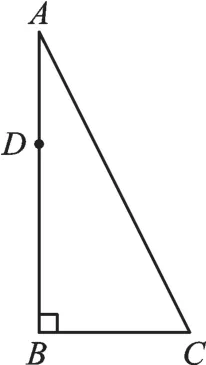
图4

【解析】Rt△ABC中，∠B=90°，则满足AB2+BC2=AC2。设AD=x，根据两只猴子经过的路程都是15m，建立等量关系，构造方程即可解决。

解：设AD=x，则AC=15-x，由BD=10，得BC=5，在Rt△ABC中，AB2+BC2=AC2，即（10+x）2+52=（15-x）2，得x=2，即AD=2，所以AB=AD+DB=2+10=12m。答略。

【归纳】方程历来是研究数学的一个重要工具。勾股定理反映了直角三角形中三边的关系，在其应用中，最常见也是最基本的一类问题就是，已知两边，求第三边，或关于此类问题的变式。方程思想在此类问题的求解过程中得到了广泛的运用。用字母表示线段，用方程解决问题，有效地沟通线段之间的数量关系，这种通过代数方法解决几何问题的策略，有助于解题思路的寻求和优化。

三、以形得数，以数定形

例3如图5，在正方形ABCD中，点E是CD的中点，点F是边BC上的一点且FC=，求证：∠FEA=90°。

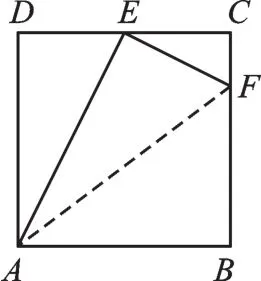
图5

【解析】勾股定理的逆定理是证明一个三角形是直角三角形或一个角是直角常用的方法。连接AF，若设正方形的边长为4a，则线段FC、EC、DE、BF的长应运而生，利用勾股定理，线段AE、EF、AF也可以用含a的代数式表示出来，再利用勾股定理的逆定理即可得结论。

证明：如图5，连接AF，设正方形ABCD的边长为4a。由题意得CE=DE=2a，CF=a，BF=3a。在Rt△ADE中，AE2=AD2+DE2=16a2+4a2=20a2。同理，在 Rt△ABF中，AF2=25a2；在Rt△ECF中，EF2=5a2。在△AEF中，AE2+EF2=AF2，所以∠FEA=90°。

勾股定理及其逆定理揭示了直角三角形的三边关系，其本身就拥有了数形兼备的特点，无论是定理的证明还是定理的运用，都充分展示了数与形的完美结合。