基于非线性制导的四旋翼轨迹跟踪控制

陈运剑,刘 畅,马武举,帅 超

(中国船舶重工集团公司 第七一〇研究所，湖北 宜昌 443003)

0 引言

四旋翼是一种能够垂直起降、空中悬停的无人飞行器，由于其机动灵活、操作简便、体积轻便等特点，四旋翼飞行器在科研、民用以及军用领域上得到了广泛的运用[1]。在四旋翼无人机的相关研究中，最为引人关注的是轨迹跟踪控制问题，也就是四旋翼能够按照一定的速度沿着预置的轨迹飞行，执行相关的任务[2]。四旋翼轨迹跟踪在民用方面可以应用于快递投送、商业表演、电力巡检等用途，在军用方面可以应用于执行无人侦察、战场巡逻等任务。

轨迹跟踪一般作为无人机控制系统的外回路，也就是导引回路，目前常用的算法主要有PID算法、反步法以及非线性制导算法等。文献[3]研究了PID算法在四旋翼无人机定点跟踪控制中的运用，通过PID位置控制并逆向求解得到所需的期望姿态来构建控制系统的导引回路。文献[4]研究了基于反步法的四旋翼无人机轨迹跟踪，通过反步法构建李雅普诺夫函数来设计无人机控制率。文献[5]研究了自适应反步法轨迹跟踪，提高了反步法轨迹跟踪器的控制精度。文献[6-7]详细介绍了非线性制导算法，并证明了其适用性。文献[8]研究了非线性制导算法中引导长度的限制问题，并通过大量仿真计算验证了其正确性。文献[9]研究了非线性制导算法在固定翼无人机中的运用，并通过自适应调整引导长度来提高轨迹跟踪的精度。

本文将非线性制导算法运用于四旋翼轨迹跟踪控制，通过构建导引回路与控制回路来实现轨迹跟踪控制器的设计，并通过Simulink构建了该轨迹跟踪控制器模型，实现了对二维以及三维复杂轨迹的跟踪仿真，分析验证了该控制器能够很好的跟踪复杂轨迹，论证了算法的可行性、正确性。

1 导引回路设计

导引回路主要任务是引导四旋翼按照期望轨迹进行飞行，具体通过非线性制导算法以及对非线性制导算法的补充部分生成四旋翼当前的加速度指令，并传递给控制回路进行姿态控制。

1.1 非线性制导算法

非线性制导算法的实现过程如图1所示。L为导引长度，通过L可以在期望轨迹上选取导引点，实现过程可以理解为以四旋翼当前位置为原点画半径为L的圆球，此圆球与期望轨迹的交点即为导引点，随着时间变化，导引点沿着期望轨迹向前运动。在控制周期里，四旋翼通过做圆周运动沿着圆弧的预期轨迹飞向导引点，随着时间的推移，四旋翼的真实轨迹逐渐向期望轨迹逼近。图中，V为四旋翼当前速度，R为做圆周运动的半径，η为四旋翼与导引点连线方向与速度方向的夹角，a⊥为向心加速度，于是可以得到如下关系：

L=2Rsinη

(1)

根据牛顿第二定律与式(1)的几何关系可以得到，四旋翼做圆周运动所需要的垂向加速度，其大小可以表达如下：

(2)

所需的垂向加速度方向通过方向向量矢量叉乘可以得到，计算过程如下：

e⊥=eV×eL×eV

(3)

式中，e⊥为垂向加速度方向单位矢量，eV为速度方向单位矢量，eL为四旋翼与导引点连线方向单位矢量。结合式(2)和式(3)可以得到垂向加速度指令的表达式，如下：

(4)

由式(4)可以看出，确定了导引长度，知道了四旋翼当前的位置、速度，就可以通过非线性制导算法得到当前的加速度指令。为了简化控制过程，在飞行过程中可以控制速度大小的不变，这就需要对式(4)得到的加速度指令进行修正。

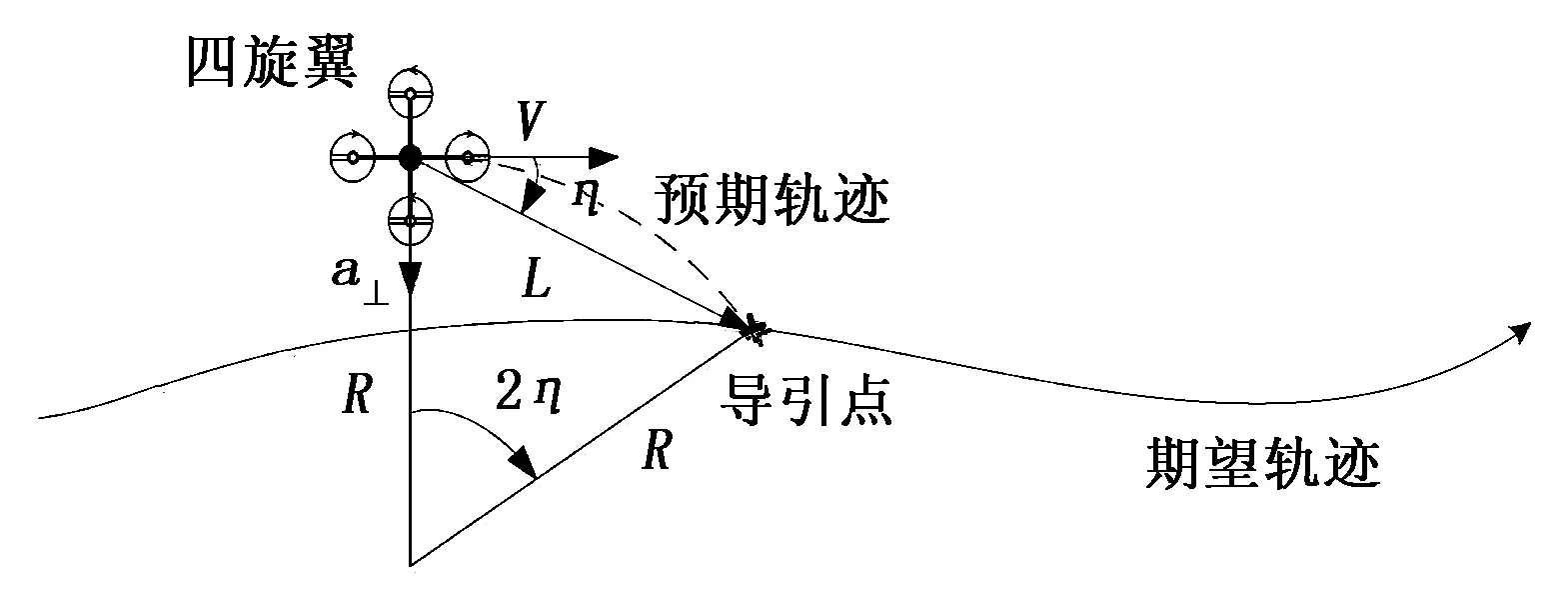
图1 非线性制导算法示意图

1.2 对非线性制导算法补充

通过非线性制导算法可以生成垂向加速度指令，理想状态下四旋翼的加速度总是垂直于速度方向，于是在飞行过程中可以保持速度的大小不变。但是由于四旋翼各通道的响应速度不同，在执行加速度指令过程中，会在速度方向上产生附加加速度，从而导致四旋翼不能保持设定的速度飞行。因此需要产生速度方向加速度指令对非线性制导算法得到垂向加速度指令进行补充修正。

本算法采用比例控制来产生速度方向加速度指令，其计算过程如下所示：

a//=KV(VS·eV-V)

(5)

式中，VS为期望速度标量，KV为速度修正系数。结合式(4)和式(5)可以得到修正后的导引回路加速度指令，表达式如式(6)所示：

(6)

通过非线性制导算法以及其补充修正设计的四旋翼轨迹跟踪导引回路不仅可以引导四旋翼沿着期望轨迹飞行，也可以控制速度大小为固定期望值。通过式(6)可以发现，导引回路的输入为期望轨迹、期望速度，输出为加速度指令，得到的加速度指令作用于姿态控制回路引导旋翼按照期望轨迹飞行。

2 控制回路设计

图2展示了四旋翼轨迹跟踪控制器结构组成，控制回路将导引回路的加速度指令信息进行逆向求解得到姿态控制指令，然后姿态控制器执行姿态指令，控制四旋翼按照期望加速度飞行。导引回路、控制回路构成了轨迹跟踪控制器的内外环，形成反馈闭环。

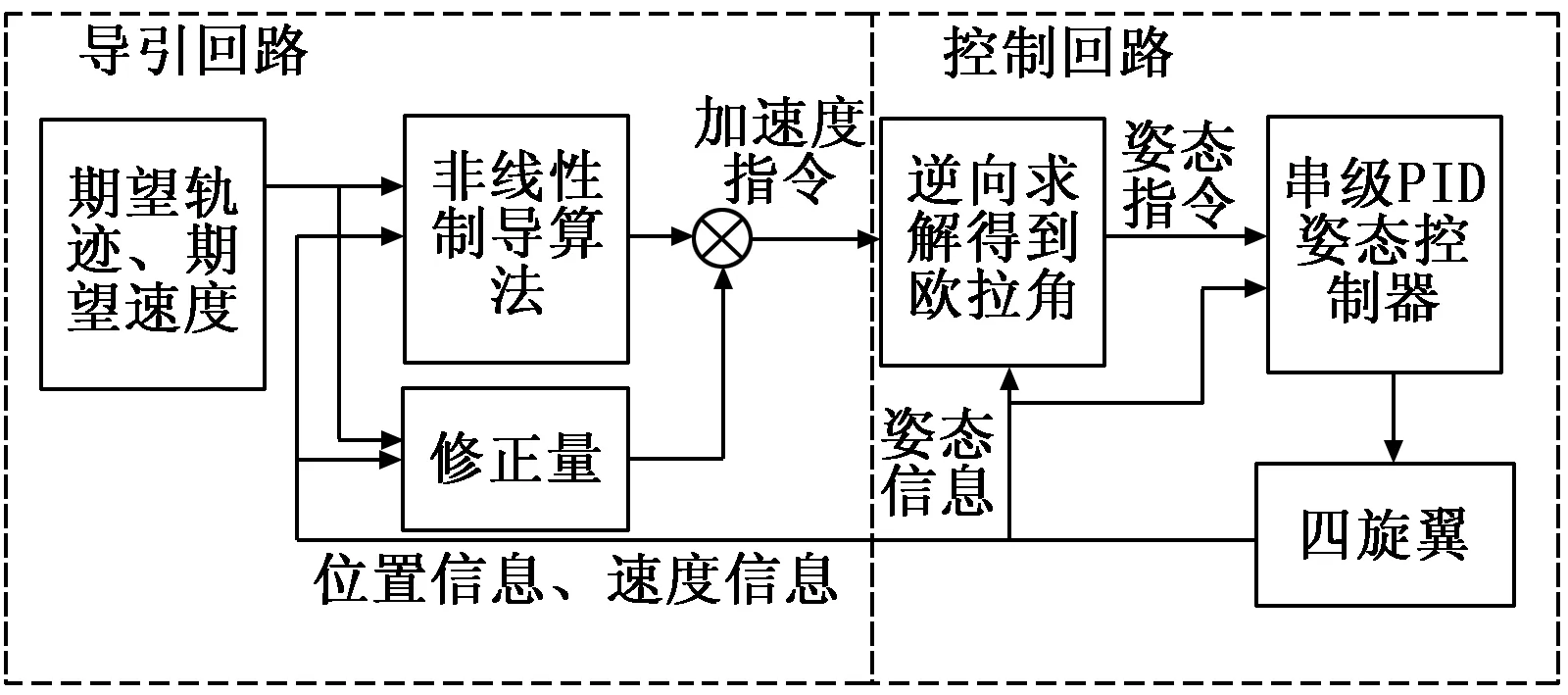
图2 轨迹跟踪控制器结构框图

2.1 逆向求解姿态指令

由导引回路得到加速度指令不能直接作用于飞行控制器，需要将其逆向求解转化为姿态控制指令，这就需要建立加速度与姿态角之间的关系，其关系可以由下述表达式进行描述。

(7)

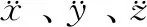
(8)

通过式(8)可以将加速度指令转换为姿态指令，在求解过程需要知道四旋翼的偏航角，在对偏航角不作特殊要求情况下为方便计算可以将其期望值设置为固定值ψS。由于四旋翼载重能力以及安全裕度的限制，需要对式(8)的桨叶拉力指令T做进一步的限幅处理，处理过程如下：

TS=Lim(T，Tmin，Tmax)

(9)

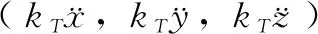
θS=Lim(θ1，θmin，θmax)

φS=Lim(φ1，φmin，φmax)

(10)

式中，θmin，θmax，φmin，φmax分别为俯仰角、滚转角限幅范围，所设计的控制器中，偏航角为期望值，因此不做限幅处理。

通过上述加速度指令的逆向求解以及限幅处理，可以得到姿态控制器能够接受的姿态控制指令(TS，θS，φS，ψS)。

2.2 姿态控制器设计

四旋翼姿态控制器的结构框图如图3所示，采用串级PID作为姿态控制算法。通过串级PID算法生成俯仰通道、滚转通道、偏航通道的控制量U2、U3、U4，高度通道控制量U1即为旋翼桨叶拉力指令TS。姿态控制量与姿态角的关系可以用下式描述。

(11)

上式为四旋翼绕质心运动的动力学方程，推导过程见文献[10]，式中，Jx、Jy、Jz为四旋翼绕机体轴的转动惯量。通过控制U2、U3、U4可以控制四旋翼的姿态。

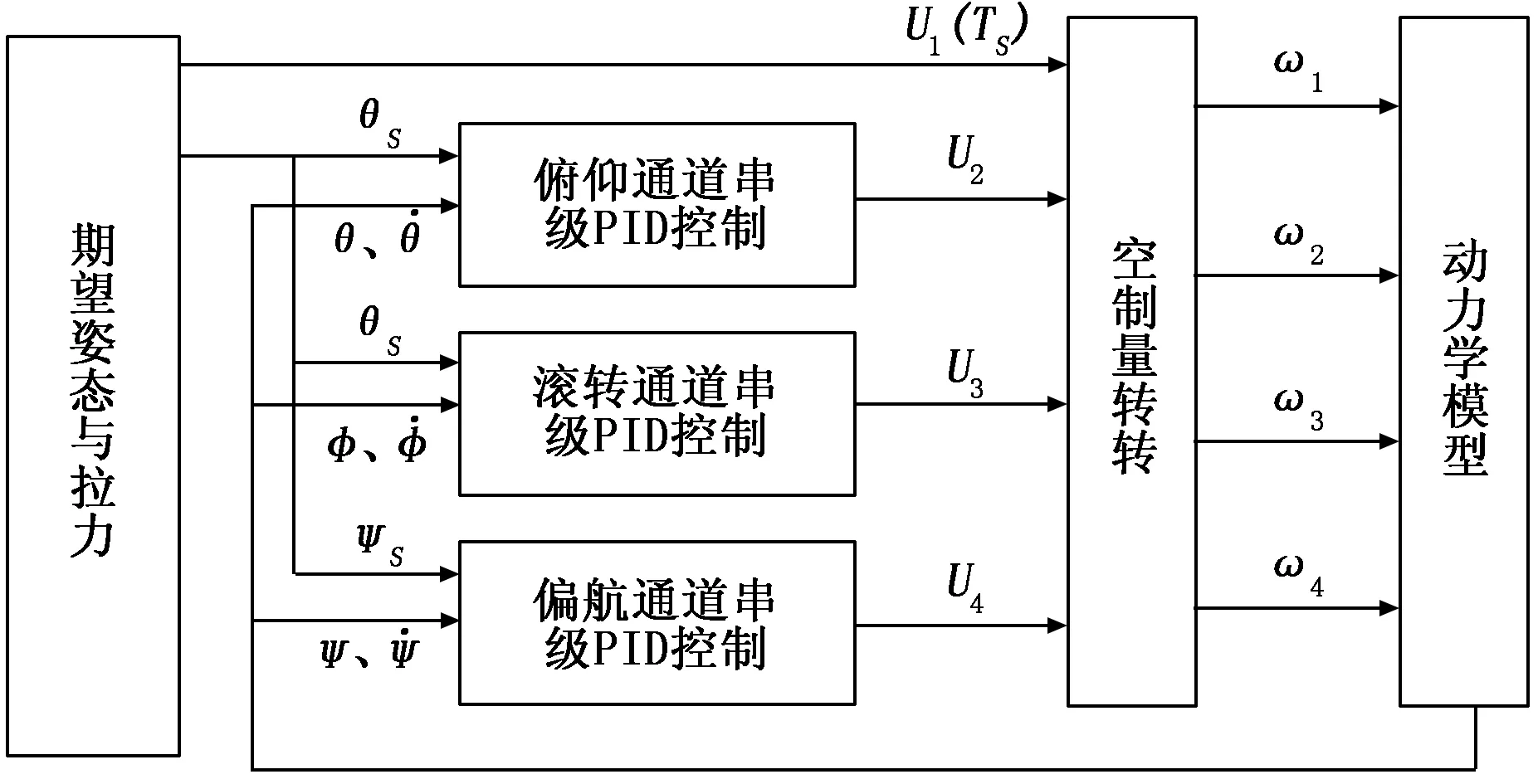
图3 姿态控制器框图

四旋翼的动力来源为四个中心对称电机的旋转，其通过改变四个电机的转速来产生偏转力矩，从而改变旋翼当前的姿态，对于“X”字型四旋翼，四个通道的控制量与电机的转速关系可以用下式进行描述。

U4=Kd(ω12+ω22-ω32-ω42)

(12)

式中，ω1、ω2、ω3、ω4为四个电机转速、d为四旋翼机体臂长，Kp为旋翼桨叶升力系数，Kd为桨叶力矩系数。

四旋翼三个姿态通道的控制信号由串级PID控制算法计算得到，以俯仰通道为例，串级PID控制框图如图4所示。

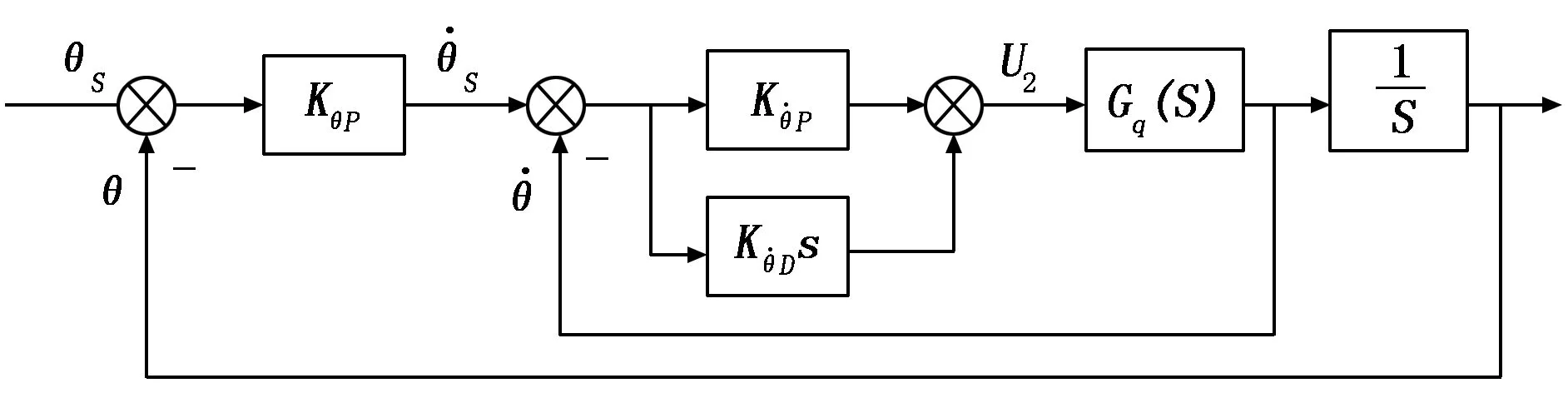
图4 俯仰通道串级PID控制框图

串级PID控制相对于单级PID，其具有更好动态特性，抗干扰性、适应性，为了获得更好的控制性能，选择串级PID算法设计姿态控制回路。本文所设计的姿态控制器，外回路控制姿态角，采用P控制得到期望角速率，内回路控制姿态角速率，采用PD控制输出期望的姿态控制量，控制方程如下：

U1=TS

(13)

控制回路将导引回路的加速度指令转换为姿态指令并进行限幅处理，最后通过串级PID算法计算输出四个通道的控制量，来控四旋翼按照期望加速度飞行，最终效果是四旋翼能够按照期望轨迹、期望速度飞行。

3 仿真验证

3.1 仿真模型搭建

采用Matlab/Simulink搭建图2框图所示的轨迹跟踪控制器来仿真四旋翼轨迹跟踪控制器轨迹跟踪效果。仿真所采用的四旋翼参数如表1所示。

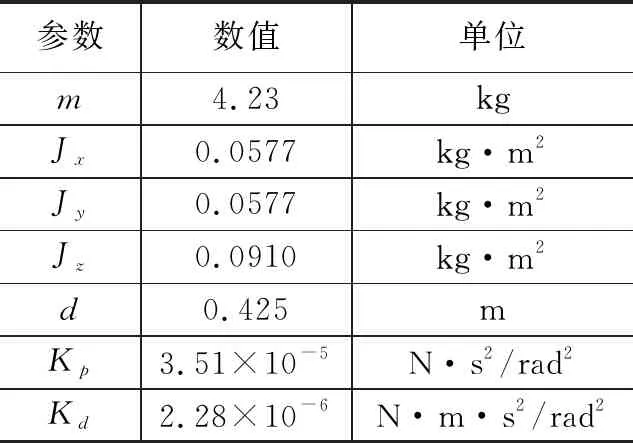
表1 四旋翼参数

轨迹跟踪控制器控制参数选取如表2所示。导引回路的控制参数L、KV取为经验值，分别为20、0.2;推力与姿态角限制取所采用的四旋翼模型的真实值；控制回路中的串级PID控制器调节参数利用工程试凑法来确定。对飞行过程中的偏航角不做特殊要求，为简化仿真过程，本文取期望偏航角为0°。

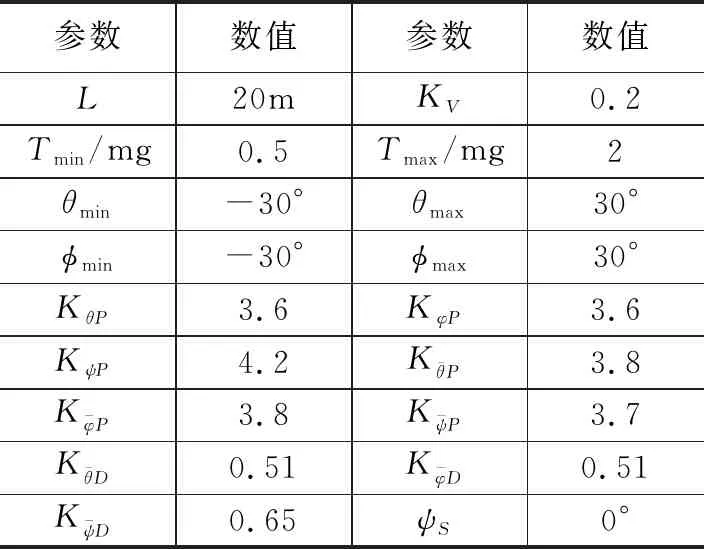
表2 控制参数

仿真的输入为期望轨迹、期望速度等，输出为实际的轨迹以及跟踪过程中的速度、加速度、姿态角等，通过对比分析真实值与期望值来验证所提轨迹跟踪方法的可行性。本仿真分为二维轨迹与三维轨迹跟踪仿真。

3.2 二维轨迹跟踪仿真

假设四旋翼初始姿态角均为0，初始位置为原点(0，0，0)，初始速度为(15，0，0)，其所需跟踪的二维轨迹为水平面内的正弦曲线，期望速度为15 m/s，期望偏航角为0°，跟踪轨迹曲线描述如下：

(14)

四旋翼轨迹跟踪控制器执行式(14)所描述的平面曲线轨迹任务时的仿真结果与相关参数如图5～8所示。由图5的轨迹仿真结果可以看出该跟踪控制器具有很好的跟踪效果，四旋翼的起始速度方向与期望轨迹所需速度方向不一致，在导引回路作用下，四旋翼的速度方向逐渐与期望轨迹所需速度方向保持一致，航迹也与期望轨迹几乎重合。由图6的距离偏差随时间变化图可以看出，除了由起始速度方向不一致导致的起始Y向距离偏差外，在执行任务航迹过程中，Y向距离偏差均维持在±0.6 m以内。由图6的跟踪速度随时间变化关系可以看出，四旋翼的速度起伏较小，基本保持在15～17 m/s内，符合速度期望，速度误差控制在2 m/s之内。

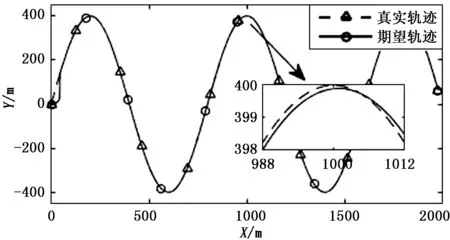
图5 二维轨迹跟踪仿真结果

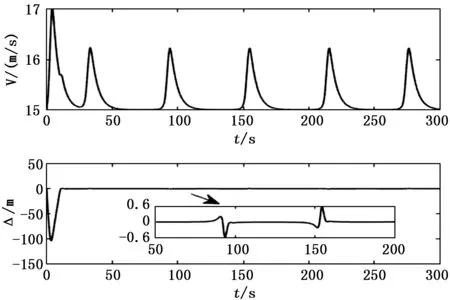
图6 跟踪过程中不同时刻的速度与距离偏差

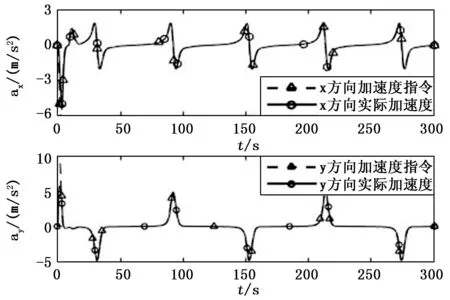
图7 跟踪过程中不同时刻的加速度

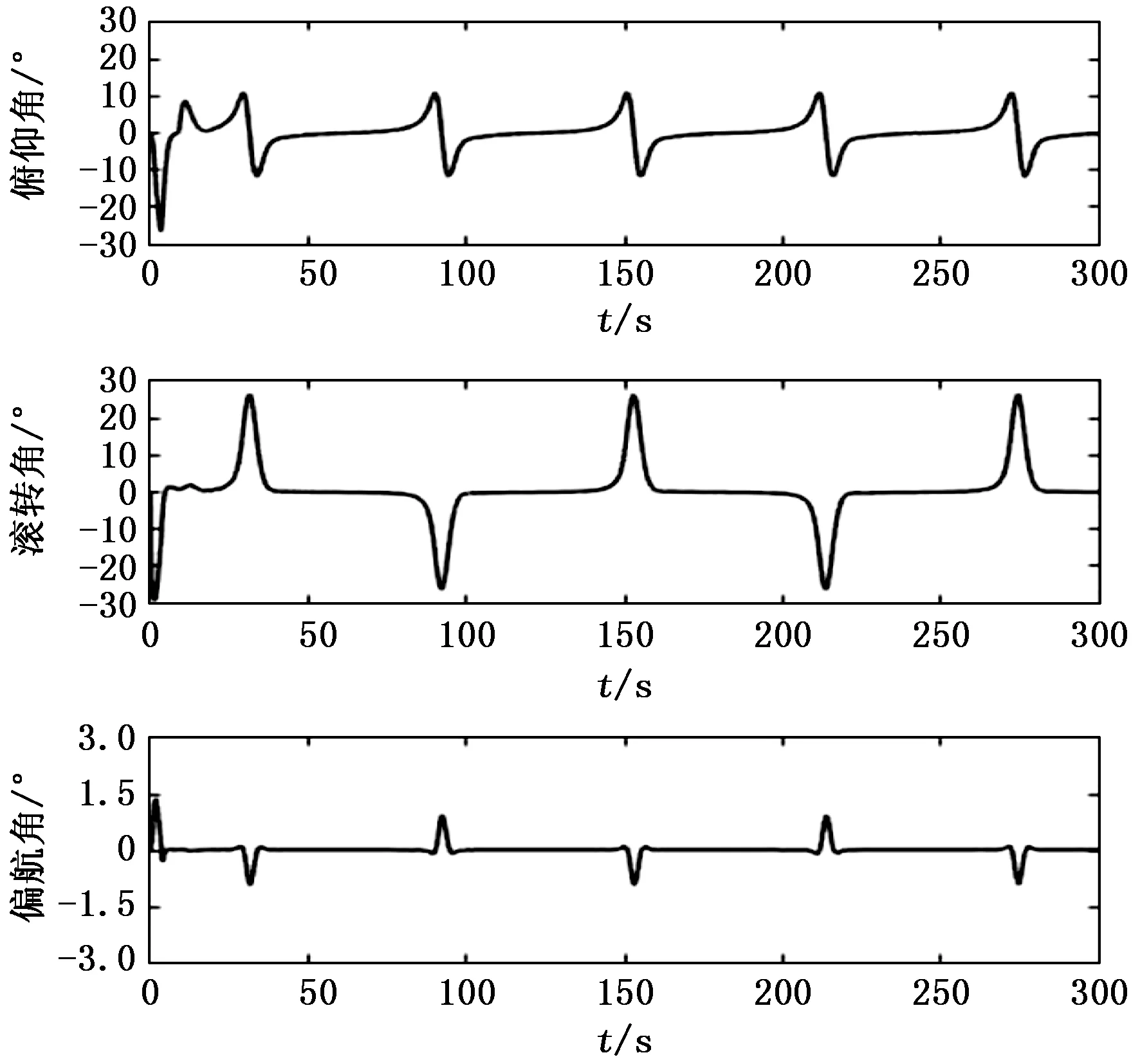
图8 跟踪过程中不同时刻的姿态角

图7为四旋翼执行航迹任务过程中的加速度曲线，可以看出实际加速度与加速度指令基本重合，部分位置实际加速度不能达到加速度指令峰值，从而导致了跟踪过程中距离误差与速度误差。从图9跟踪过程中姿态角变化曲线可以看出，滚转角与俯仰角均没有超过姿态角限制(-30°，30°)，而偏航角保持在-2°～2°以内，基本符合偏航角的期望0°，所设计轨迹跟踪控制器在满足姿态限制要求的前提下，保证了了轨迹跟踪精度。跟踪过程中加速度、姿态起伏变化较剧烈的点发生在任务轨迹拐弯处，这符合运动学和动力学规律。

通过上述二维轨迹仿真结果可以发现，所设计的轨迹跟踪控制器能够对正弦复杂轨迹进行精确跟踪。

3.3 三维轨迹跟踪仿真

为了验证所设计的四旋翼轨迹跟踪控制器执行更复杂曲线任务的能力，对三维曲线轨迹进行跟踪控制仿真。四旋翼的初始条件与3.1节所述条件相同，其所需跟踪的轨迹为三维空间里的正弦曲线，可以通过下述曲线方程进行描述。

(15)

轨迹仿真结果以及相关参数如图9～11所示。由图9的轨迹仿真结果可以看出所设的轨迹跟踪控制对三维轨迹也有很好跟踪效果，除了在拐弯处，真实轨迹与期望轨迹基本重合。由图10跟踪过程中速度变化曲线可以看去，跟踪过程速度维持在15～17 m/s，速度误差小于2 m/s。由图10的距离偏差变化曲线可以看出，除了起始0 s、50 s、100 s左右范围时间段存在较大的距离偏差，在整个跟踪过程中，距离偏差不超过±4 m。在0时刻范围处存在较大偏差是期望轨迹所需速度方向与实际速度方向偏差较大导致的，相当于起始误差。

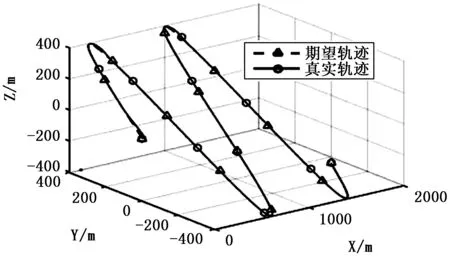
图9 三维轨迹跟踪仿真结果

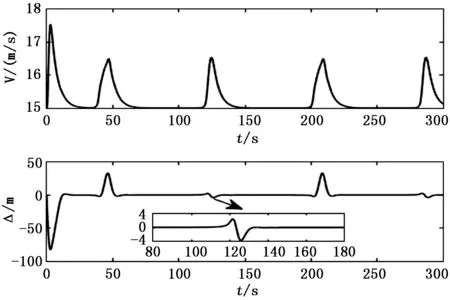
图10 三维轨迹跟踪过程中的速度与距离偏差

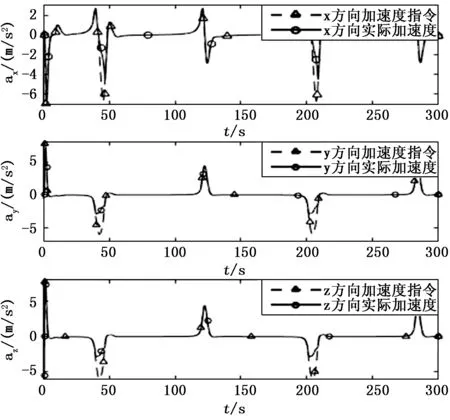
图11 三维轨迹跟踪过程中不同时刻的加速度

结合分析图11的加速度曲线，可以看出在50 s、100 s左右范围时间段内，三个方向的实际加速度与加速度指令存在较大的偏差，这就导致了在50 s、100 s时间段范围出现较大距离偏差。可以发现在上述两个时间段，四旋翼刚好处于轨迹的波峰处，此时x、y方向的加速度指令需要有较大的升力，而z方向的加速度指令需要有较小的升力，这种矛盾是四旋翼自身控制方式(升力的分量产生侧向控制力)导致的，控制器执行加速指令的过程如式(9)、(10)，对得到推力指令和姿态指令进行限幅处理，因此此处的加速度指令与实际加速度存在较大偏差。

通过三维轨迹仿真可以发现除了受自身控制力限制的飞行段外，所设计的轨迹跟踪器能够对复杂的三维轨迹进行精确跟踪。

4 结束语

本文采用补充改进的非线性制导算法设计了四旋翼轨迹跟踪控制器的导引回路，采用串级PID算法设计了控制回路。仿真分析结果表明，该轨迹跟踪控制器有很好的跟踪效果，既能跟踪二维复杂轨迹，也能跟踪三维复杂轨迹；在跟踪过程中，能维持速度与偏航角在期望值附近；在满足姿态角与推力限制条件下也能有很好跟踪效果。导引长度是本文所提四旋翼轨迹跟踪控制器的关键控制参数，其大小对轨迹跟踪效果的影响以及其取值范围是后续研究的方向。