CCD双轴自准直仪的长距离测量实现

王星星 周小全 吕斌

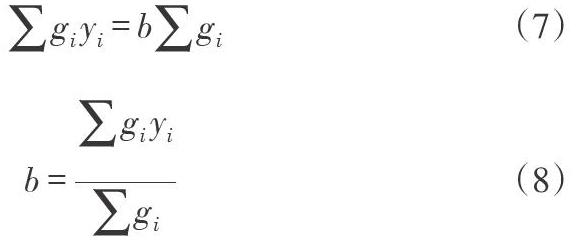
摘 要：本文阐述了一种基于面阵CCD的双轴自准直仪的长距离测量方法。其间利用上位机对十字叉丝的图像处理结果与德国ELCOMAT 3000测角真值进行比较，验证光学系统的测角精度，并采用灰度重心法与最小二乘法相结合的算法，使定位精度达到亚像素级。分析结果显示，在±10″内测量精度优于0.2″，在±100″内测量精度优于3″。试验结果表明，该方法具有较高的实用价值。

关键词：面阵CCD;双轴自准直;长距离测量;亚像素

中图分类号：TH741.14文献标识码：A文章编号：1003-5168（2020）29-0059-03

Abstract： This paper described a long-distance measurement method of a dual-axis autocollimator based on an matrix CCD. In the meantime， the image processing results of the cross hairs by the upper computer were compared with the true value of the German ELCOMAT 3000 angle measurement to verify the angle measurement accuracy of the optical system， and an algorithm combining gray barycentric method and least square method was used to make the positioning accuracy reach the sub-pixel level. The analysis results show that the measurement accuracy is better than 0.2" within ±10"， and the measurement accuracy is better than 3" within ±100". The test results show that this method has high practical value.

Keywords： matrix CCD;dual-axis autocollimator;long-distance measurement;sub pixel

CCD自準直仪是目前测量微小角位移的常用计量精密仪器之一。借助平面反射镜，通过与细分多齿分度台相互配合，CCD自准直仪被广泛用于多面棱体、经纬仪检定装置、角度块等量具的测量[1]。自准直仪具有较高的测量精度和准确度，所以被广泛应用于精密的测量领域，比如，在导轨的直线度测量、角度测量、轴系的角晃动测量、平板的平面度测量等方面，其发挥着重要的作用。同时，随着应用领域的不断扩大，人们开始不仅仅满足于对自准直仪测量精度及量程等指标的要求，而且在实现长距离测量方面有更多的需求。因此，从事CCD自准直仪长距离测量方面的研究具有重要的实际意义。

1 系统组成及其原理

1.1 CCD自准直仪测角系统

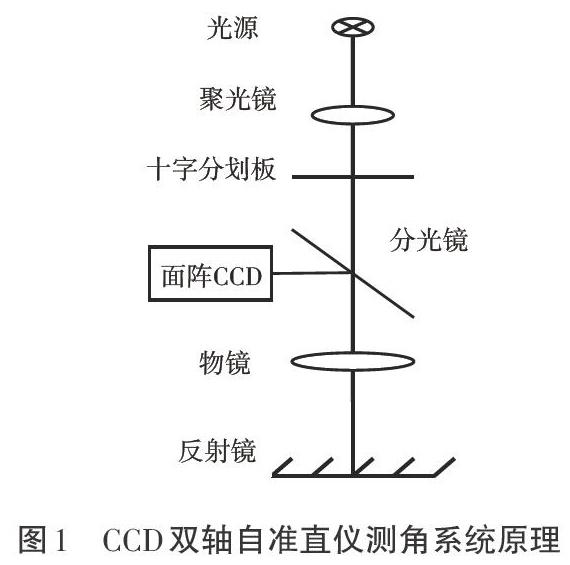
CCD自准直仪测角系统主要由光学机械结构和上位机两大部分构成，其中光学机械结构由光源、聚光镜、十字分划板、分光镜、物镜、反射镜和CCD相机组成，上位机主要实现图像的采集、数据处理以及实时显示X与Y轴的角度值等功能。系统原理如图1所示。

如图1所示，CCD自准直仪LED发出光源，此光源借助聚光镜和十字分划板，最终在平行光管内形成一束平行的十字光源。发出的十字光源与发射镜面交汇，反射回CCD自准直仪内，由CCD图像感光芯片记录发射光信号，通过图像采集系统将视频信号传输给PC机，由PC机实现图像信息保存和图像处理，从而达到计算十字像二维位移的目的。

1.2 测角系统数学模型

由于CCD传感器芯片设计工艺的限制，它的最小象元尺寸无法满足现今角度测量精度的实际要求[2]。为此，人们开始关注亚像素分割技术的研究。像素细分的方法有以下几种：灰度重心法、抛物线拟合法、高斯内插法[3]。本文采用的是灰度重心法与最小二乘法相结合的算法。

十字光源成像到图像传感器上时，其为两条具有一定宽度且相互垂直的交叉线。如图2所示，图中[AB]为其中一条直线的中心线，设[AB]的直线方程为：

得到每条光线的中心点后，运用最小二乘法拟合得到两条光线的中心线，然后利用虚拟出的两条直线，即可得到其相交点，从而得到十字像的中心位置。

测角光路图如图3所示。当反射镜有微小的角度[θ]移动时，反射光线和入射光线夹角偏移2[θ]，因此像[o′]相对于反射镜垂直于光轴时的像[o]偏移[x]位移，此时可以得到[x]位移的计算公式为：

式中，[f]为CCD自准直仪的物镜焦距;[θ]为发射镜的角度偏移量。

其中，[θ]可以用公式表示为：

分别计算得到[x]、[y]轴的位移偏移量，通过式（10）即可得到发射镜面相对[x]、[y]轴的角度偏移量，从而达到[x]、[y]双轴角度测量的目的。

2 试验结果及误差分析

目前，可用于自准直仪的光电转换器件主要有面阵CCD、线阵CCD、四象限光电探测器、PSD四种[4]。本文采用的是基于面阵CCD的光电转换器件，分辨率为1 296×966，像元尺寸为3.75 μm×3.75 μm。

平行光管是第一层传感，把几何量的变化转化为平行光管中十字分化线位置的变化;CCD摄像机把十字分化线位置图像信息变成视频模拟信号;图像采集卡在驱动程序的作用下把CCD摄像机的视频模拟信号变成数字图像信息;数字图像信息经过计算机系统的处理（包括图像的预处理、二值化、微分、拟合及细分），图4表示的是反射镜离光管15 m处CCD相机获取的十字像。显然，随着测量距离的增加，获取的十字像的尺寸逐渐变小，而且光叉丝的宽度随之变细，这点是CCD自准直仪实现长距离的难点之一。

由于德国穆勒公司生产的EL COMAT 3000自准直仪的测量精度较高，笔者利用新设计的远距离自准直仪与穆勒光电自准直仪进行了比对试验，表1是二者间距为15 m时的测量结果。其间，焦距f为300 mm。

由于篇幅的关系，表1只列举了负方向上的测量角度。从表1可看出，研制的CCD双轴自准直仪可以测量到-200″。为了直观地显示自准直仪的测量效果，利用MATLAB软件对表1数据进行处理，图5表示试验之后得到的穆勒自准直仪和试验样机的测量结果以及误差。其中，Bastler2表示的是试验样机测量结果。

从图5可以看出，在15 m测量距离时，除个别点外，试验样机在10″范围内的测量误差优于0.2″，在100″测量范围内误差优于3″，同时，随着测量角度的增加，试验样机相对穆勒光电自准直仪的测量误差增大。

3 结语

本文介绍了一种CCD双轴自准直仪实现长距离测量的方法，并建立了基于灰度值重心法和最小二乘法相结合算法的亚像素分割数学模型，得到了在15 m测量距离时自准直仪样机的测量精度及量程。该光学系统结构简单，采用角度测量算法，其在Visual C++编程软件中易于实现。

参考文献：

[1]邹九贵，甘俊红，季国定.高精度二维自准直仪的研制[J].新技术与新仪器，2006（5）：19-26.

[2]郑友琴，袁旭军.用CCD实现精密长度测量[J].电测与仪表，1998（35）：45-47.

[3]王雯倩，刘国栋，浦昭邦，等.利用面阵CCD测量小角度的研究[J].光电技术应用，2004（2）：134-138.

[4]黄伟成.基于线阵CCD的边缘测量及重构技术的研究[D].武汉：武汉理工大学，2008.