“可能性”教学纪实与评析

田丽 赵国会

教学内容：人教版小学数学五年级上册。

教学目标：

1.通过摸球活动，学生能初步体验事件发生的确定性和不确定性。经历猜测和简单的验证，初步感知可能性是有大小的。能用“一定”“可能”“不可能”来描述生活中一些事情发生的可能性。

2.结合具体情境，能对某些事件进行推理，概括其结果，形成初步的判断、推理能力。能对一些简单事件的可能性进行描述。

3.在游戏中感受数学学习的快乐，并获得一些初步的数学实践活动经验;在和同伴交流的过程中获得良好的情感体验。

教学重、难点：体验事件发生的确定性和不确定性。能通过对数据的简单分析，初步感知可能性的大小。

教学过程：

一、揭示主题，直接导入

师：同学们，今天老师要和大家一起上一节数学课。（出示课题，学生读课题。）游戏大家最喜欢了，这节课我们就在游戏中边玩边思考，看看游戏里还隐藏着哪些数学知识。

二、了解事件发生的确定性

1.体验“一定”。

师：在开始我们的摸球游戏前，须要指定一个记录员，谁来？

（生应答，师递给学生一支笔。）

师：考考你，如果摸到一个白球怎么记录？再摸一个呢？（明确记录环节。）

师：我们现在就开始玩游戏。谁愿意来摸？这个游戏是我们共同完成的，所以大家的任务是他摸完之后，迅速说出球的颜色。

生：红球。

师：继续摸。（摸4次。）

师：记录员请你汇报一下摸球的结果。

生：摸4次的结果都是红球。

师：谢谢你，请大家根据这个摸球结果猜一猜，如果继续摸会摸到什么颜色的球？

生：（共同猜测。）红球。

师：到底猜得对不对？咱们一同验证一下。（师倒出1号袋子里的球。）

生：都是红球！

师：都是红球怎么了？

生：因为口袋里没有别的颜色的球，所以只能摸到红球。

小结：是啊，口袋里全是红球，伸手任意一摸，就一定摸出红球。（板书：一定。）

2.感受“不可能”。

师：老师这里还有一个口袋，谁还想摸？（走到学生中间任意找4～5名学生快速摸球。）

师：记录员准备——

师：记录员请你汇报一下摸球的结果。

生：摸到了2次黄球3次白球。

师：再来猜一猜，如果继续摸会摸到什么颜色的球？

生：可能是黃色，也可能是白色。

师：还有不同意见吗？

生：还可能摸到红球。

生：不可能摸到红球，因为前5次从来都没摸到红球，口袋里一定没有红球。

师：到底可不可能摸到红球呢？我们再来看看袋子里的球。（师倒出袋子里的球。）

师：可不可能摸到红球？

齐答：不可能。（追问：为什么？）

生：因为口袋里原本就没有红球 ，就不可能摸到红球。

小结：对呀，从一个没有红球的袋子里想摸出一个红球，这简直是天方夜谭，是绝对不可能的。（板书：不可能。）

师：刚才通过两轮摸球游戏，我们准确判断出了两个袋子里球的颜色。还想继续猜猜吗？

三、验证不确定现象

1.猜测可能性大小。

师：在我们的生活中大多数事件都是我们无法提前预知的不确定现象，就像这个口袋里已经有7个红球了，现在我再放进去3个黄球。你觉得现在让你来摸一次，只摸出一个球，你摸出来的结果会是——

生：可能是红球也可能是黄球。

师：为什么会是这样？（板书：可能。）

生：因为只有这两种颜色的球。

生：但红色球被摸到的可能更大，因为红色球有7个。

师：他在用数据描述事实，并进行了一次猜想，谁也有这种想法？（生举手。）

师：好，既然你们有自己的猜想，那么就让我们来验证一下吧！

2.验证可能性大小。

师：课前，老师给每个小组都准备了一个袋子，里面都装了这样的10个球。我们实际摸一摸，验证一下我们的猜想。注意听清要求。（课件出示：游戏规则。）

（1）爱心提醒。

A.摇一摇、摸一摸、说一说、记一记;

B.共同提出猜想，一人负责填写记录单，其他几人轮流摸球;

C.每小组共摸球20次。

师：要求清楚了吗？现在游戏开始！

师：看来大家都摸完了，来汇报一下你们得到了什么结论。

（2）汇报典型数据。

板书：三种情况：A.红多黄少    B.红黄一样多     C.红少黄多

生：哪种颜色球数量多摸到的次数就多。

验证：7红3黄。共摸20次，我们小组摸到了红球15次，黄球5次。

结论：我们从记录中发现，红球数量多，摸到的次数就多，可能性大，黄球数量少，摸到的次数就少，可能性小。

师：同学们，我们知道口袋里一共有7红3黄，他们小组的结果很好地验证了我们的猜想，有没有哪个小组与他们的结果不一样？

生：我们小组摸到红球9次，黄球11次。我们发现红球数量多，摸到的次数少，可能性小，黄球数量少，摸到的次数多，可能性大。

师：还有哪个小组的结果也不是红多黄少？

师：我们小组各摸到了10次，结论就是虽然红、黄球数量不同，但摸到次数相同，可能性也相同。

师：后两个小组的验证结果与第一小组的不一样，与我们的猜想也不同，是谁错了呢？

师：我们在小组内先说一说你们的想法。

生：虽然两种球个数不一样多，但是也有可能摸到的次数相同。

生：我认为大多数情况哪种球多摸到的次数就更多。

生：我不同意，虽然口袋里红球多，但你要是运气好，就可能摸到的黄球多。

师：老师希望生活中你们都有好运气。他提到的运气，其实就是我们摸球中的随机性，而前一名同学也说了“大多数”一词。

生：就算是口袋里只有一个黄球，也可能摸到的黄球次数多。

师：噢！你们表述真清晰，大家要表达的意思老师听明白了，每次摸球随机出现的情况都会不同，即使是可能性很小的情况，也是可能出现的，所以会出现这两组的结论。看来如果我们只凭这一两组数据是无法验证我们的猜想的，那怎么办呢？

（3）整理全班数据。

生：我认为那就把更多数据加在一起来验证，就会有一定的准确性。

师：好，那我们把其他小组摸球的数据和发现也汇报一下，我们统计到一起再来看一看。

（小组逐一汇报。）

师：来看看我们全班汇总的结果。

生：总计摸球200次，红球131次，黄球69次。

师：恩，这个数据比我们一个小组的数据要大很多啊，200次的数据很好地支持了我们最初的猜想——红多黄少。

3.感受数据的随机性。

师：这是咱们刚刚现场摸球200次收集的数据得到的结论，如果是1班同学也来摸200次，是不是也会得出和咱们班一样的数据呢？说说你的想法。

生：可能一样，也可能不一样，因为每个小组摸出的数据不同，那么总数就有很大概率是不同的。

师：你还提到了概率呢，看来同学们的数学学习越来越深入了。

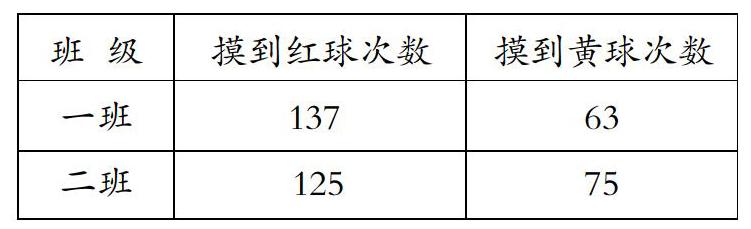
师：老师上课之前分别带来了一班和二班的摸球数据，让我们一同看看。

出示：口袋里有7个红球3个黄球，摸球200次结果。

师：观察了三个班级的摸球结果，你有什么想说的？

生：通过我们班级和另外两个班级的数据分析，能够看出红球的个数多，被摸到的次数也多。

生：我发现红球占7/10，黄球占3/10，摸到红球的概率占393/600，摸到黃球的概率占207/600，可见摸到某个球的概率和这个球占总数的多少是有关系的。

师：你真善于用数据来说话！看来随着摸球次数越来越多，越能得到“黄球的数量多，被摸到的可能性大”这一结论是正确的。

师：如果现在把红球增加到9个，黄球减少到1个，你认为还可能摸到黄球吗？

生：可能，只是被摸到的可能性比较小。

师：那如果红球增加到999个，黄球还是1个，还能摸到黄球吗？

生：还是有可能的，不管有多少个红球，只要是还有一个黄球，就有可能摸到黄球，只是可能性会越来越渺茫了。

师：表述真严谨，只要有一个就是有可能的。看来，按照这样的规律，我们根据摸到球的次数，也能推断口袋里分别有几个球。

四、运用规律做出合理推断

1.进行第三次摸球活动，统计摸球次数并做判断。

师：既然每种球所占的个数与摸到的次数之间存在着一定的联系，那是不是我们知道了两种颜色的球被摸到的次数的多少，就能推断出它们的数量呢？

生：我觉得只能大概看出谁多谁少，并不能看出有多少个。

师：他认为不能具体知道。

生：我认为基本能够做出判断，就像我们上面摸出的那些数据一样。

生：但我们三个班级摸出的数据不能说明全部。

师：似乎都有道理啊，能与不能我们还得去证实一下。

师：同学们拿出2号口袋，这里面有红球、黄球共20个，让我们一同验证一下吧！我们来看具体要求。谁来读一读？

生：要求：①每组口袋里的红球数量一样多，黄球数量也一样多。②每次摇匀摸出一个，记录后再放回。③完成数据统计并猜一猜每种球的个数。

师：听明白了吗，下面开始吧！

师：看来大家都已经完成了，我们一起汇报。

生：我们小组摸到红球的次数是13次，摸到黄球的次数是7次，我们认为红球多。

师：这是他们的结论，有不同意见吗？

生：我们小组摸到红球的次数是8次，摸到黄球的次数是12次，我们认为黄球多。

师：他们两个小组的观点截然相反啊！我们先继续，还有不同的意见吗？

生：老师，我们小组摸到红球和黄球的次数一样多，我们组认为袋子里的两种球的个数一样多。

师：又出现了三种不同结论，能判断吗？

生：不能。

师：那怎么办？

生：收集更多数据再观察。

师：同学们已经用好了这个办法，那就让我们把所有小组的数据都统计在一起。

2.由大数据推断具体数量。

（板书：全班统计：红球147次，黄球53次。）

师：用现在全班统计的数据来分析，你能做出一个合理的判断吗？

生：（齐答。）红球多。

师：你们推断出了红球多，那么能准确推断出每种球的个数吗？

生：能。

师：不要着急，现在老师又带来了咱们全年级摸球次数的统计，谁来读给大家听？

生：五年级共摸球1800次，摸到红球1235次，摸到黄球565次。

师：这回我们的数据就更大一些了，你能不能根据数据来推测一下红球和黄球分别是多少个？

生：我认为红球有14个，黃球有6个。

师：你是怎样推测的呢？

生：我是根据之前摸到这些球的倍数关系，感觉大概应该是红球有14个，黄球有6个。

师：你已经对数据有一个直观感受，并能够去分析了。还有其他答案吗？

生：我感觉红球有13个，黄球有7个。

生：我也认为红球有14个，黄球有6个。

生：也可能是15个红球，5个黄球。

师：同学们，我们先不猜了，到底有多少个呢？让我们一同揭晓谜底吧，打开口袋验证一下你的推测结果是否正确。（生欢呼。）

师：怎么？用欢呼声来庆祝你们的胜利吗！

生：答案和我们的猜测一样，红球有14个，黄球有6个。

师：值得庆祝！但即使没有完全准确推断出具体数量的几名同学同样优秀，你们通过收集、整理、分析大数据已经很接近于真实情况，这就是统计在我们生活中的价值所在。

五、总结

师：同学们，数据虽然不能张口，但我们却能让它表达，因为我们能读懂它，只要我们收集到足够多的数据，通过整理、分析就能从中发现规律，做出接近事实的推断，并给我们的现实生活带来帮助，这就是数据的魅力。

评析：

本节课的设计重在让学生亲身经历数据收集和整理的全过程，感受统计的随机性，通过贯穿课堂始终的摸球游戏，发展学生数据分析观念，帮助学生建立起“用数据说话”的意识。让学生在经历过程中明白，同样的事情，每次收集到的数据可能会是不同的;也让学生明白，当数据足够多时，可以从中发现规律，进而用部分数据来推断总体情况，让学生最终把握统计的随机本质。

1.亲身经历，形成数据分析意识。

数据分析意识的建立，必须伴随着学生的亲身经历。本节课中三次摸球活动的设计贯穿课堂始终，集体摸球，共同记录分析，以小组为单位摸球并记录分析，学生亲身经历了数据收集的全过程，其价值不仅仅是凸显了数据收集的“客观真实性”，更为体会“随机性”提供了真实的实践感知。这份感知是其他任何一个学习活动都不能替代的。学生亲身经历的越多就对数据的变化感觉越敏感，其最终的推断准确率也会越高。对“一定”“不可能”与“可能”的理解在环节设计上层层深入，在思维水平提升上节节拔高。

2.分析整理，感知统计的随机性。

随机思想的最大特征就是结果的不确定性，是学生从“确定数学”进入“随机性数学”的重要铺垫和台阶。让学生感受到无论每种颜色球的多少，每一个球被摸到的可能性是均等的、随机的，所以收集的数据会是不同的。第三次摸球，反推口袋中每种不颜色的球的数量时，让学生在过程中明白，对于同一件事情，每一次收集到的数据可能是不同的，这只是随机性主要含义的第一个层面，更为重要的是要在足够多的数据中发现隐含的规律，这才是对随机思想的深层次理解。

3.实事求是，培养学生科学精神。

本节课的教学环节设计尊重学生的思维发展水平和认知规律，在验证“哪种球数量多摸到的次数就多”这一结论时，充分让学生发表自己的观点。当“球的数量多摸到的次数却少”这一观点呈现时，不仅体现了统计的随机性，教师的这种预设也是对学生的价值引领，培养学生实事求是的科学精神，让学生懂得数据有随机性，而且可以有误差，但必须真实。在最后一环节中让学生学会用数据说话，更是教学中教育性的一种体现。

教学建议：

本节课教师通过让学生体验收集、整理、分析数据，形成初步的数据分析观念。但对数据越大越能接近事实本身的验证过程中，教师设计了同年级几个班级的数据累加，在教学过程中可以看到，学生依然存在疑惑，依然认为数据不能完全支撑结论。若在此环节借助信息技术手段，可以实现用数以万计的数据进行分析，便能更深入地理解抽象化的分析过程，更加明确统计、分析为决策和推断提供依据的道理，达到形成数据分析观念，并发展学生数学思想的目的。

编辑/魏继军