面向医疗文本数据压缩的主流算法及发展趋势*

2020-12-05高克承

中国医学装备 2020年11期

高克承徐桓刘岩刘洋张曦*

大数据时代，信息产出量成指数型爆炸增长，不断增长的数据量对于信息的存储和传输造成极大困扰，深刻的影响着多个行业和领域。医疗卫生方面，随着患者的不断增加及医患关系的交流深入，与之相关的医疗文本的数字化势在必行，由此引发一系列重要问题：一方面，医院常年累月的运转会产生庞大的医疗文本数据，应如何存储如此庞大的数据量；另一方面，随着远程医疗和网络诊断的出现及应用，需要存储和传输的医疗文本信息量与日俱增，以上信息又该以何种方式存在。

当前，医疗文本信息的存储和传输已逐渐成为国内多数医院亟需解决的难题之一，迫切需要一种适合于医疗卫生领域的文本压缩算法改善此难题。调研并阅读文本数据压缩类文献，阐述各类经典文本压缩算法的简单原理，发掘近年来文本数据压缩算法的新发展，尝试分析和探索适用于当前医疗文本数据的压缩算法。

1 经典文本压缩算法

1948年，信息论之父香农提出了“香农编码”，自此数据压缩方法层出不穷，各种变体衍生而出[1]。立足于文本数据压缩问题，依次介绍三种经典的无损压缩算法，即Huffman编码、串表压缩算法(Lempel-Ziv and Welch，LZW)编码和基于部分匹配预测(prediction by partial matching，PPM)的压缩算法，并分析各算法的优缺点。

1.1 基于Huffman编码的文本压缩算法

Huffman编码是由Huffman DA于1952年提出的一种基于统计概率模型的经典压缩算法[2]。其运行机制类似于摩尔斯(morse)电码机，每个字符的编码只有几个比特序列，即利用初始信号出现的概率进行编码，常出现的信号编码较短，不常出现的信号编码则较长。

Huffman编码基本上是一个表示为二叉树的前缀码(prefix code)。二叉树的左分支标记为0，右分支标记为1，从根到叶的每个路径上形成的比特序列是用于匹配对应字符的前缀码，如此形成的二叉树称为Huffman树[3-4]。算法如下：①计算所有信号的频次并排序得到集合；②取最小两个频次的信号组成左右Huffman树放入原来的集合中；③重复②中的内容，直到集合只剩一个元素时结束；④根据树枝的左边为0，右边为1的规则进行编码，结束。

文本压缩算法是一种最佳编码方式，码不唯一，平均码长相同，但不影响效率和压缩性能，但也具有以下缺点：①码长参差不齐，存在输入和输出速率匹配的问题，可设置缓冲器；②误码存在连续传播；③编码效率和压缩比率受输入信号影响；④必须与其他压缩算法相结合来提高其过低的压缩比率。

1.2 基于LZW编码的文本压缩算法

1977年，以色列的Lempel和Ziv共同提出了查找冗余字符及用较短的符号标记代替冗余字符的技术，简称LZ压缩技术。1985年，美国的Welch将LZ压缩技术从概念发展到使用阶段，简称LZW压缩技术，广泛应用于文本压缩领域。

LZW编码又称“串表压缩算法”。是一种对字符串进行编码的同时生成特定字符串及与之对应的索引字符串表的无损压缩算法[5]。LZW压缩算法流程见图1。

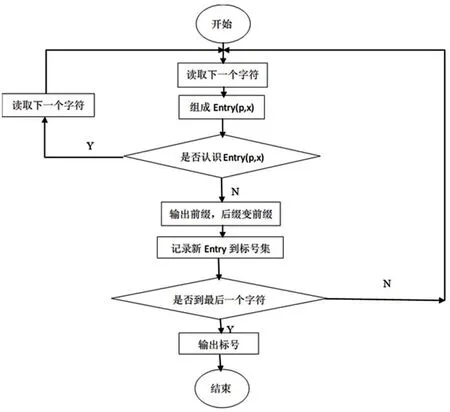
图1 LZW压缩算法流程图

LZW压缩使用字典库查找方案，其读入待压缩的数据并与一个字典库(库开始是空的)中的字符串作对比，如有匹配的字符串，则输出该字符串数据在字典库中的位置索引，否则将该字符串插入字典中，该算法特点如下：①有效利用了字符出现的冗余度，字典自适应生成，位置冗余度利用不足；②对可预测性不大或在数据流中反复出现的字符处理效果较好；③可用于图像压缩，实现迅速压缩和解压缩；④可处理大量数据的同时对计算机硬件性能要求不高。

1.3 基于PPM的文本压缩算法

1.3.1 PPM文本压缩算法

PPM算法是一种基于上下文的统计建模技术，采用有限数量并且已知字符的标准马尔可夫模型(Markov model)进行近似预测[6-8]。通过一系列不同顺序的上下文模型预测下一个即将出现的字符，一个新的字符出现在上下文中时，该字符将会自动获取一个转义概率，根据转义方法的不同出现许多PPM的变体[9-11]。

PPM模型简要论述如下：令A是由|A|>2组成的离散字符表，且D为该模型的最大阶数，其中d(d≤D)为当前该模型的编码阶数。即将出现的字符xn+1=φ，φ∈A的概率取决于当前的上下文Sd=xn，…，xn-d+1。字符φ在上下文Sd中出现的概率为：

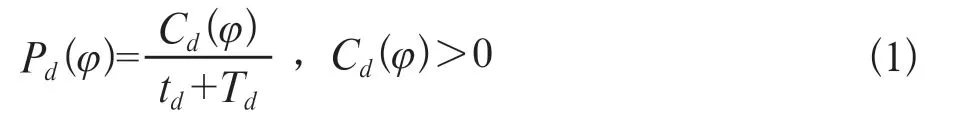
式中Cd(φ)表示字符φ在上下文Sd中出现的次数，Td=∑Cd(φ)表示上下文Sd被访问的总次数。字符φ在上下文Sd中出现的转义概率为：

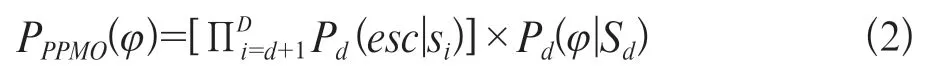
式中D是该模型的最大阶数，d(d≤D)是当前该模型的编码阶数PPM建模技术与算数编码相结合的编码方式具有高压缩比率，但过于占用内存且执行速度较慢。

1.3.2 PPMO中文文本压缩算法

PPMO是一种适合于中文文本的压缩算法，由Wu和Teahan提出[10]。编码过程分为两部分：顺序流和符号流[12]。顺序流为每个编码符号输出一定的编码顺序；符号流是基于特定的上下文顺序输出编码符号本身。简要阐述该算法的编码过程。

(1)若一个符号φ在一个上下文模型Sd中已出现过，则对顺序流中当前最大的d进行编码，而后是符号本身的符号流将采用以下公式进行编码：

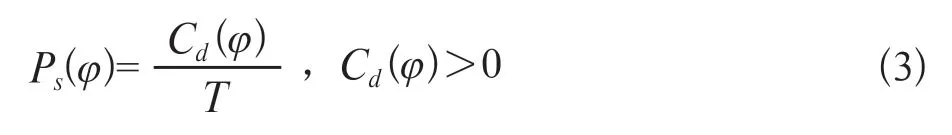
式中Cd(φ)表示字符φ在上下文Sd中出现的次数，T表示上下文Sd被访问的总次数。

(2)若一个符号φ并未在上下文模型Sd中找到，将会倒退回上一级寻找，直到按照需要返回默认的-1序列为止。为确保一个符号总能在-1序列里面找到，在字母表中给每一个符号分配一个数字标志。选择用于编码符号的模型后，首先对模型顺序进行编码，而后再使用该模型对符号进行编码。

由于顺序流具有较小的字母表尺寸和重复性，使其成为一种高度可预测的编码方式。如若一个上下文模型的符号流的最大编码顺序是2阶，对于顺序流而言，其可能的情况仅有4种，即{-1，0，1，2}。以下为中文版《圣经》的顺序流样例：

1,2,0,1,0,1,2,2,0,0,1,0,1,2,1,0,0,0,0,0,0,0,1,2,0,0,0,1,1,0,1,2,2,-1,0,1,0,0,0,1,2,2,0,1,-1,-1,0,1,0,0,1,0,-1,0,-1,0,1,2,0,1,2,2,0,1,2,1,0,-1,0,-1,0,1,0,0,-1,0,0,1,0,0,1,0,1,2,2,2,2,2,2,2,2,2,2,2,0,1,2,0,1,0，可将顺序d视为要编码的一个单独的实体，接着使用传统的PPM编码方式对该顺序进行编码。则顺序d的条件概率为：

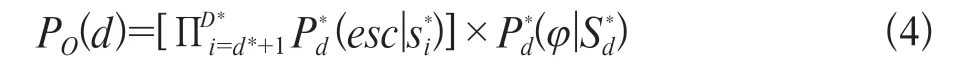
式中D*表示顺序流的最大编码顺序；d*≤D表示当前的编码顺序；表示当前顺序流编码的上下文，符号φ的总编码概率为：

式中PO(d)是顺序d的条件概率，Ps(φ)是符号φ本身的符号流。

Wu及Teahan[13]的实验显示，小文件的压缩率为7.350 bpCc，大文件的压缩率为5.938 bpCc，比GNU zip及bzip2压缩软件压缩率高，该算法优点体现在转义频率低和执行速度快，缺点为每个字符都需要两步的编码。

上述数种经典压缩算法是目前文本压缩的主流算法，其对于小文件可做到无损且快速压缩。由于当前医疗文本数据的海量化，上述算法逐渐展现疲态，面对大量医疗文本数据，会出现压缩速度慢、耗时长及准确率下降的缺点。因此，为满足目前医疗文本压缩需求，探索可压缩海量文件的新型压缩算法势在必行。

2 文本压缩算法新进展

由于社会数据量的爆炸增长及存储的海量化，一些新型压缩算法应运而生。简要阐述基于压缩感知的文本压缩技术，并对机器学习和深度学习用于文本压缩的可能性进行讨论。

2.1 基于压缩感知的海量文本压缩

压缩感知(compressed sensiong，CS)是一种新兴的压缩方法，常用于图像压缩，近年出现了压缩海量文本的方法[14-16]。压缩感知理论指出：只要信号是可压缩的或在某个变换域是稀疏的，便可用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上，然后通过求解一个优化问题即可从这些少量的投影中以高概率重构出原信号，可证明该投影包含了重构信号的足够信息[17]。在该理论框架下，采样速率不再取决于信号的带宽，而在很大程度上取决于两个基本准则：稀疏性和非相关性，或稀疏性和等约束性。

2.2 基于压缩感知理论的海量文本压缩

研究的压缩对象主要是社交媒体平台，如推特(Twitter)、脸书(Facebook)和亚马逊(Amazon)的用户生成内容，旨在解决两个问题：①应如何管理和存储数量巨大且不断变化的文本数据流；②如何从文本数据流中获得高质量的文本。

文本流如社交媒体等用户生成的文本流有两个压缩过程：①根据指定的多样性参数为每个文本段生成高质量的文本集合；②降维压缩上述集合。简要阐述上述两个过程：

(1)高质量文本集合生成。一般而言，一个句子或一篇文章的质量通常取决于其所包含的术语的重要性，这是已广泛应用于在线趋势主题检测和高质量微博提取的基本原理[18-19]。将一个术语的重要性定义为其在一个片段中的出现频率，文本的质量定义为其所包含的所有术语的熵。因此，对一系列的文本段{抽象为文本术语矩阵X1，X2，…，Xl，…[∈R(n·Pl)(l=1，2，…，L，…)]}，第l段第i个文本的质量由熵E(i，l)所决定：

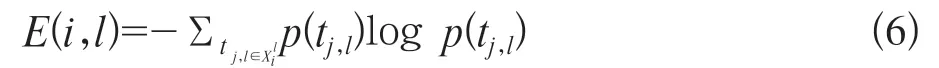
基于文本熵，通过从文本段中选择次优文本集合来生成高质量文本集合，以使其对应于选定的分集参数值(以ω表示)。令文本段Xl按照熵的降序排列，由一个空白的文本集合Xl(ω)开始从Xl中选择第一个文本，接着迭代的从Xl中添加直到在Xl(ω)中的熵的范数小于给定的ω。最后，生成一个高质量的文本段落Xl(ω)(这些文本的熵值之和大约等于分集参数ω)。

(2)线性测量的文本压缩。在一般的CS框架中，并不是获取信号x∈RM×N的N个样本，而是通常将M个随机测量值称为以CS编码获取的随机投影，其中M＜N。由欠定的线性方程组表示：

式中y∈RM×1是已知的测量向量；∅∈RM×N是随机测量矩阵。

该算法框架下，每个高质量文本段Xl(ω)(l=1，2，…，L，…)以压缩感知理论为基础进行压缩。对于给定的一个线性测量矩阵∅，通过以下公式获得Xl(ω)中的样本矩阵Yl(ω)∈Rm×Pl(l=1，2，…，L，…)：

采用一种基本的循环编码方式，将压缩成一系列样本片段Y1(ω)，Y2(ω)，…，Yl(ω)，其中Yl(ω)远远小于Xl(ω)。此外，每个段的单词表被保存从而进行后续的解压缩操作。与原始文本流相比，此样本段的存储所需消耗的内存空间要小得多且更便于传输和检索。

Gaussian随机矩阵的实体满足一个独立且同一的高斯分布，均值为0，方差为(i.e.，∅ij～N(0，))，满足该条件的矩阵被用于测量线性矩阵∅。已经证明，只有在满足m≥cK log(+1)，c>0的条件下才能从样本Y中恢复出信号X。该压缩方法压缩率高、速度快且解压缩误差低，缺点为算法是有损压缩。目前，已证明该算法可用于压缩社区聊天，经过改善将有可能成为一种适合于海量医疗文本压缩的新型算法。

2.3 机器学习和深度学习用于文本压缩的可能性

机器学习和深度学习用于文本压缩较为新颖，目前可能存在一些不太成熟的方法，但关于机器学习用于医学图像的高密度压缩的方法已出现[20]。其基本思路如下：①构建一个可识别图像中关于人体器官或组织中的关键元素的智能学习模型；②提取出上述关键元素并存储；③填充图片仅剩背景图，接着将其压缩存储。如上述将特征单独存储，同时将不重要的背景图层压缩后，得到的即为压缩后的医学图片。针对于医疗文本，探索是否可模仿图像压缩方法，首先构建一个智能学习模型，该模型可提出医疗文本中的关键元素，同时筛选出相关主要特征，最后将主要特征进行存储，得到压缩后的文件，类似主成分分析法(principal components analysis，PCA)，解压缩时根据提取的主要特征进行还原[21]。如结合PCA和机器学习，有可能建立一种医疗文本压缩算法。

目前关于深度学习的压缩主要集中在视频及医学图像的再压缩[22]。方法是先训练出一个准确的卷积神经网络(convolutional neural networks，CNN)标准数据集，再对视频进行切割分类，最后进行压缩。由于当前医院的医疗文本信息量足够多，可训练出类如前文所述的CNN数据集。可借鉴医学图像再压缩方法，首先训练一个CNN数据集，再对医疗文本进行有效的切割分类，最后进行压缩。