预埋式注灌装置充水过程水力特性数值模拟

杨 笑，李 琳，张 军

（新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052）

1 研究背景

预埋式注灌装置是一种适用于果树灌溉的加压地下灌水器，该技术于2011年获得发明专利[1]。预埋式注灌装置是在新植果树时将装置的出水管预埋至果树根系附近，供水系统提供的水流流经田间管网输水系统进入预埋式注灌装置的进水管从而对装置进行注水，注水时管中的气体一部分通过出水流道侧壁的出水孔排出，一部分仍残留在流道中与水流混掺形成水气两相流，当水流流进预埋在果树根系附近的出水管时，装置即可通过出水管侧壁上布设的出水孔向果树根区灌水[2]，具体结构如图1所示。王兴鹏等以1350株试验枣树为研究对象，将预埋式注灌装置与滴灌灌水器进行了节水增产对照试验，试验结果表明，采用预埋式注灌装置对枣树根部进行加压注水灌溉，较滴灌灌水器节水效率增加50%以上，增产9.09%[3-4]。与地面灌水器相比，预埋式注灌装置属于地下灌溉技术，可直接将水输送至果树根系，可有效解决地面灌溉造成的土壤板结[5]、次生盐渍化[6]及根系生长不良[7]等问题。

近年来，滴灌、喷灌等各类高效地面节水灌溉技术发展迅速，研究人员通过试验研究和数值模拟针对地面灌溉技术的水力特性和灌溉性能进行了系统研究[8-11]，但国内外对地下灌水技术的研究较少。蔡耀辉[12]提出了微孔陶瓷灌水器应用参数确定办法，构建了微孔陶瓷根灌系统，并在田间进行了初步应用；王栋[13]研制了防堵塞内镶贴片式地下灌水器。在预埋式注灌技术推广应用中发现果树根区土体局部冲刷严重、灌水均匀度低、湿润体与果树根系空间分布吻合度不高这一系列问题，致使预埋式注灌装置未能得到广泛的应用。因此，为了弄清楚预埋式灌水器对土体局部冲刷严重的原因，本文基于试验研究和数值模拟的方法对预埋式注灌装置充水过程的瞬变流水力特性开展研究，研究成果可望为优化预埋式注灌装置结构体型，减少出流对果树根区土体冲刷提供指导，对预埋式注灌装置在干旱区节水灌溉领域进一步推广提供技术支撑。

图1 预埋式注灌装置结构示意图

2 数学模型

2.1 控制方程预埋式注灌装置流道内的水流流动可视为黏性不可压缩流体的流动，基本控制方程为连续性方程和动量方程，具体见式（1）和式（2）。

式中：ρ为流体密度，kg/m3；ui、uj、uk（i，j，k=1，2，3）为各时均速度分量，m/s；p为流场的时均压强，Pa；μ为流体的动力黏度，（N·s）/m2；δij为Kroneker符号（当i≠j时，δij=0）；为脉动应力分量。

2.2 紊流模型k-epsilon Realizable湍流模型对标准k-epsilon模型进行了改进，引入了一个更为合理的黏度公式和一个新的能量耗散率传输方程，该方程不再基于假设而是由一个准确的涡流脉动传输方程推导而得[14]。该模型可表示为：

式中：k为湍流动能；ε为湍流动能消散率；μ1为层流涡黏系数；σk、C1ε和C2ε为模型常数。

VOF（Volume of Fluid）模型适用于求解分层流动和自由表面流问题，如计算空气和水不能互相融合的流体流动。在VOF模型中，当控制体内气相流体的体积分数α=1，即该控制体内无水，被气相充满；当α=0时，表明控制体内被水充满，无气相；当0＜α＜1时，控制体同时被水相和气相充满[15]。气相体积分数α的控制微分方程为：

式中：α为气相的体积分数；ρα为气相密度；ρw为水相密度。

3 计算区域的离散及边界条件

本文模拟的预埋式注灌装置的尺寸为：进水管水平段长度0.3 m，竖直段长度0.8 m；两水平出水管长度均为0.3 m；两出水管夹角为90°。管道内径0.036 m，每根出水管侧壁布设5个出水孔，出水孔直径0.003 m，相邻两出水孔间距0.05 m。计算区域的网格划分均采用六面体单元和四面体单元，进水管与出水管交汇处采用四面体单元与边界层六面体单元，边界层网格过渡比为0.272，网格增长率为1.2，层数5层，在出水管上对出水孔网格局部加密，整个装置中最小网格单元的体积为9.7×10-13m3，控制方程的离散采用有限体积法。从稳定性、精度性和适用性方面考虑，选择时间项离散为二阶迎风格式，对流项离散为QUICK格式。离散后的线性代数方程组采用交错网格下的PISO算法迭代求解，计算时间步长为1×10-4s。

进口采用压力进口边界，为便于进行数学模型验证，进口压强值与预埋式注灌装置的物理试验的压强值相同。在实际应用中，预埋式注灌装置的出水管埋设于地下，出水管及出水孔均被土体包围，土体类型及土体含水率会对出水孔的出流环境产生一定影响，当土体含水率较大时，在出水孔周围形成饱和区，进而会产生一定的正压[16]，出水孔外界压强大于大气压强，出水孔出流类似于淹没出流。由于本文重点关注预埋式注灌装置充水过程的水力特性，且本文模拟的预埋式注灌装置的充水时长短，孔口周围土体的含水率在短时间内尚未形成饱和，水压力较小，因此，本文对出口边界条件进行了简化，将出水孔口按照自由出流考虑，采用压力出口边界，压强大小与大气压相同为101.32 kPa。壁面采用无滑移边界，近壁处的黏性底层采用标准壁面函数进行处理。当t=0 s时，控制体内气相体积分数为1，进口水相体积分数为1。由于出水管为对称出水，故仅在过右侧出水管管轴线的纵剖面上，距离出水孔中心水平距离0.01 m、铅直距离0.018 m的近上壁面位置布置监测点，按照出水管内水流流经的顺序，分别将出水孔顺序编号为1′—5′，监测点依次编号为1—5。

4 计算结果与分析

4.1 数学模型验证为了对本文的数学模型进行验证，在实验室内对本文模拟的预埋式注灌装置开展了进口压力不同、恒定流条件下的出水口出流量测试研究。试验系统布置如图2所示。试验系统由供水水泵、进水口处压力表、预埋式注灌装置组成。通过供水水泵对预埋式注灌装置进行有压充水，充水过程中装置流道内的气体通过装置底部出水管侧壁布设的出水口排出，各孔口出流流入集水槽。待装置进水口处压力表读数恒定不变后，流道内形成恒定流。由于孔口出流量较小，采用称重法量测孔口出流量，多次测量后把所得流量数据进行整理对比，规定每组的流量相对差值在±3%以内时数据为有效数据，对有效数据求平均值，该值即为恒定流条件下预埋式注灌装置的出水流量。物模试验工况及其出水流量结果如表1所示。

图2 试验系统布置图

表1 预埋式注灌装置孔口出水流量实测值与数模结果对比

应用2.1节的数学模型对进口压强分别为10～40 kPa下的装置恒定流条件下的出水流量进行模拟。将数值模拟的孔口出流量和实测流量值进行对比，计算其相对误差结果见表1。从表1中可以看出，各工况条件下数值模拟计算结果与物理试验数据最大相对误差不超过5%，计算结果与物理试验数据吻合较好，表明本文采用的数学模型及其经验参数适用于预埋式注灌装置流场特性计算。

4.2 网格无关性分析考虑到网格数量对计算结果的影响，文中采用了4种网格划分方案对计算区域进行离散，方案1、方案2、方案3和方案4的网格总数分别为27万、32万、46万和70万。在进口压强为13.8 kPa时，对预埋式注灌装置充水过程中的水气二相瞬态流动进行数值模拟，比较了不同网格剖分方案下装置内的最大压强值，结果如图3所示。从图3中可以看出，网格数量增加至46万和70万时，装置内最大压强值的差值为0.8774 kPa，两方案计算结果的偏差率仅为1.94%，表明网格数量大于46万时，网格数量对计算结果基本没有影响，因此，本文的后续模拟采用了网格剖分方案3，网格数量为46万。

图3 不同网格剖分方案下计算最大压强值

4.3 结果分析图4（a）所示为预埋式注灌装置右侧出水管各出水孔附近监测点的压强随时间变化曲线，P/P0表示监测点的瞬时压强与进口压强的比值。从图4（a）可以看出：（1）在充水过程中及充水结束后5个监测点处的压强值及其随时间的变化规律基本一致，均呈现出压强随时间先增大，后产生剧烈波动，最后稳定趋于定值的规律，这主要是因为预埋式注灌装置的出水管长度仅为0.3 m，距离短，从1到5号监测点压降很小。（2）t=0～0.4 s，压强随时间缓慢增大，各监测点的压强值均小于预埋式注灌装置的进口压强，P/P0＜1；t=0.43 s时，各监测点的压强值由进口压强的0.5倍陡增至2.7倍，此后压强随时间产生剧烈的波动，出现多个波峰和波谷；t=0.668 s时，各监测点均出现压强极大值，大小为进口压强值的3.27倍；t＞0.9 s后，出水流道内水流流态变为恒定流，监测点处压强随之稳定，由于流道内水流混掺气体形成水气两相流，监测点处压强略大于进口压强。

图4 充水过程中1—5号监测点的压强和1′—5′号出水孔流量瞬时变化过程

图4（b）所示为预埋式注灌装置右侧出水管各出水孔口流量随时间变化曲线，Q/Q0表示各孔口的充水过程的瞬时流量与充水结束后的恒定流时的流量比值。从图4（b）可以看出：（1）由于孔径一定时，孔口出流大小取决于孔口的压强水头，故5个出水孔在充水过程中的流量变化规律与对应监测点处压强变化规律一致。（2）瞬时流量随瞬时压强的波动而波动，压强波峰和波谷值对应流量波峰和波谷值。以5号监测点为例：P/P0＜1时Q/Q0＜1，P/P0＞1时Q/Q0＞1；t=0.575 s时，瞬时压强在波动过程中出现极小值，5′号出水孔的瞬时出水流量也为充水过程中的最小值，大小为恒定出流的73%；t=0.668 s时，瞬时压强在波动过程中出现极大值，5′号出水孔的瞬时出水流量也为充水过程中的最大值，大小为恒定出流的1.66倍。显然，充水过程中出水流道内反复出现的极端压强势必会使出水口的流量瞬时陡增，孔口出现喷射流，造成出水孔周围的局部土体严重冲刷。

为了弄清楚出水管道内极端压强出现的原因，并考虑到注灌装置出水管道为对称出流，以右侧出水管为例对充水过程中水气二相体积分数、气团分布位置随时间的变化规律进行分析。图5中选择了压强波动达到极大值时刻及其前后时刻的水气二相分布结果进行讨论，图中蓝色代表气体，红色代表水，介于红色和蓝色之间的是水气混合物。从图5可以看出：t=0 s时，水流尚未充入管道，管道内仅有气体相，管道内压强为0；t=0～0.43 s时，水流充入出水管，出水管内气体体积减小，水流动能转化为压能，管道压强增加；t=0.43～0.575 s时，出水管末端的气团一部分通过出水孔排出，一部分在水流的挤压作用下向出水管上游运动，t=0.575s时出水管末端已无气体分布，对比t=0～0.43 s时段，出水管内气体体积分数持续减小，但出水管内压强并未呈现持续增大的规律，这是由于出水管末端水体对后续充入的水体起到水垫消能的作用，并且部分被末端水体反弹的水流沿上管壁运动一段距离后撞击分布于出水管下半管的水体，对充水产生阻力，因此，t=0.43～0.575 s时出水管内压强降低；t=0.575～0.668 s时，气体体积分数继续减小，水体几乎充满整个出水管，水流动能转化为压能，出水管内压强增大；t=0.668～1.0 s时，气体体积分数与水体体积分数几乎不再发生变化，t=0.9 s后水流流态达到恒定流状态，压强稳定不再产生波动。

图5 充水过程中出水管道纵剖面水气二相分布

图6所示为注灌装置出水管的10个出水孔的排气量和出水流量随时间变化的规律。从图6可以看出：（1）t=0～0.3 s时，受充水影响，出水孔的排气量从0陡增至1.6 L/s，而出水流量为0。随充水过程延续，管道内气体体积减小，水体体积不断增大。当0.3＜t＜0.7 s时，排气量从1.6 L/s减少至0.15 L/s，出水流量从0增至0.32 L/s。t=0.7～0.9 s时，由于残留气团随流输移，使出水流量产生波动，t=0.8 s时压强小于恒定流状态下的压强值，对应的出水流量0.26 L/s，略小于恒定流时的出流量0.29 L/s，t＞0.9 s排气量趋近于0，出水孔出水流量趋于恒定值。（2）预埋式注灌装置的排气过程主要集中在0～0.4 s，t=0～0.3 s时，出水管内压强逐渐增大，在压力作用下管内气体经出水孔被排出，排气流量逐渐增大；0.3 s后出水孔为水气两相出流，水流充入出水流道，随着不断充水，出水管内水体体积分数增大，残留气体沿上管壁流动，出水孔处气体量减少，排气流量逐渐下降。充水过程中出水管内压强波动引起出水流量波动，当出水管内瞬时压强增大时，瞬时出水流量随之增大，出水管内瞬时压强减小时，瞬时出水流量减小。

图6 出水孔排气流量&出水流量变化曲线

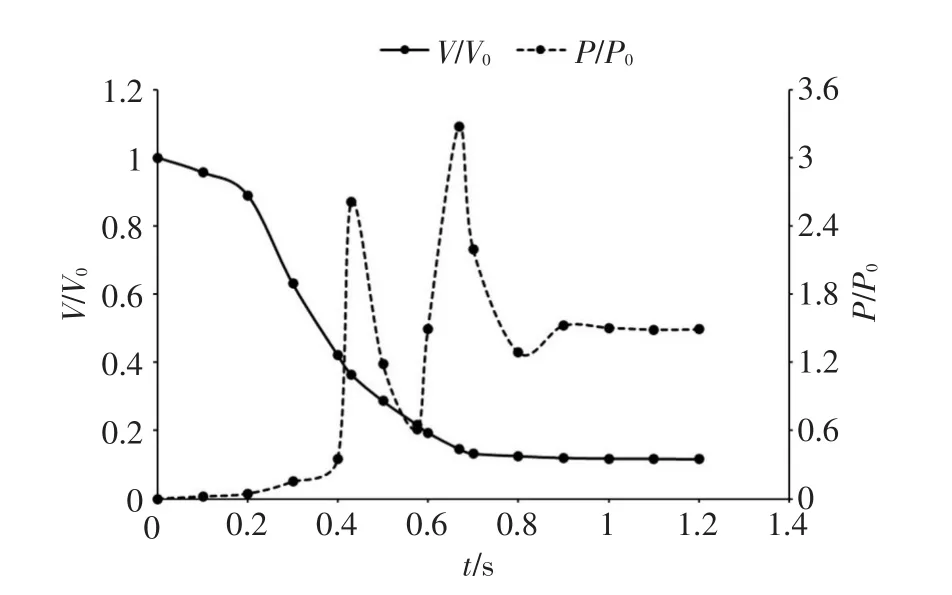
图7 充水过程中装置内气体体积及5号监测点压强变化过程

图7所示为预埋式注灌装置内残留气体体积及5号监测点压强随时间变化曲线。图中左纵轴坐标V/V0表示装置内瞬时气体体积与初始时刻气体体积的比值；右纵轴坐标P/P0表示5号监测点的瞬时压强与进口压强的比值。从图7可以看出，自充水过程开始，气体体积分数随压强增大而减小，t=0.2～0.668 s，气体体积衰减速度最快，压强在该阶段反复出现极值。表明排气速度越快，越容易反复出现压强极值，进而引发孔口射流，造成土壤局部冲刷。

5 结论

（1）预埋式注灌装置充水过程为瞬变流，t=0.4～0.9 s，出水流道的瞬时压强剧烈波动，随水流的充入出现峰值和谷值交替出现的规律，t=0.668 s时出现最大瞬时压强值，是装置进口压强的3.27倍。t=0.9 s后充水结束，出水流道内水流为恒定流，压强趋于恒定值。

（2）预埋式注灌装置充水过程中出水孔的出水流量随时间的波动变化规律与压强变化规律一致，t=0.4～0.9 s瞬时出水流量发生剧烈波动，瞬时压强峰值对应瞬时出水流量峰值，最大瞬时流量值是恒定流状态下出水流量的1.66倍。充水结束后出水流量稳定，趋于恒定值。

（3）预埋式注灌装置在充水过程中反复出现大于进口压强的峰值，使出水孔产生大于恒定流状态下出水流量的瞬时流量峰值，引发孔口射流，造成了出水孔周围的局部土体严重冲刷。

预埋式注灌装置的出水孔位于地下，周围为土壤，充水过程中土壤含水率迅速增加，使出水孔处的实际压强大于大气压强，孔口出流的实际水头小于自由出流时的水头，因此，其充水过程中的最大瞬时压强值会因实际工作水头的减小而小于本文模拟的自由出流时的瞬时最大压强值，但对其压强和流量的波动规律影响较小，故本文结论应用于工程实际参考时偏于安全。