基于正交试验的翼片式斜板沉沙池截除率研究

赵法鑫，李 琳，杨力行，郑祖国

（1.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052；2.浙江水利水电学院 水利与环境工程学院，浙江 杭州 310018）

1 研究背景

翼片式斜板沉沙池是是由日本学者丹保宪仁在一系列试验后提出的一种新型水沙分离技术，又被称为迷宫式沉沙池，其结构是在斜板上布置与水流方向垂直的翼片（如图1所示），水流流经翼片形成三个区域：主流区、涡流区、环流区。泥沙颗粒在涡流区的作用下被带入翼片槽内，槽内环流区流速远小于主流区，为泥沙沉降提供了良好的水力条件。在涡流和环流的共同作用下实现水沙的动态分离。李继震[1]研究了横向流翼片式沉淀池内沿深度方向浊度的变化规律，结合水平方向除浊公式，提出了包含水平、竖直两个方向的除浊数学模式。He Cheng等[2]通过CFD数值模拟对翼片式斜板沉沙池内的流场进行了研究，分析发现水流在流经翼片后形成的涡流区可将主流区的泥沙颗粒送入环流区，泥沙颗粒在环流区内增加了碰撞几率有助于沉降，并通过模型试验验证了在沉沙池内布置翼片式斜板可有效的提高截除率。胥标[3]采用湍流雷诺模型及离散相模型对翼片式斜板沉沙池内水沙两相流进行了模拟，分别就翼片格数、翼片宽度、斜板宽度和斜板倾角各单因素对截除率的影响做出了研究，得到了沉降效果最优时的结构参数。倪建华[4]将翼片式斜板应用于含沙量较高的长江以及嘉陵江的取水头部，对粗沙细沙和粗细沙在不同进水流速下进行除沙效率及结构参数优化试验，得出对除沙效率影响较高的因素为断面流速、翼片斜板尺寸、倾角和翼片格数等。赵法鑫等[5]通过对三种不同沉沙池的各种表面负荷下的截除率进行试验，证明了翼片式斜板沉沙池截除率的优越性，且在翼片式斜板沉沙池中已沉降的泥沙不易受水流影响再次悬浮流出沉沙池。陈滨[6]在镇江市金山水厂翼片斜板沉淀池内进行原型试验，分析了进水均匀性、絮凝效果和翼片格数对去浊效果的影响程度。

图1 翼片式斜板流区示意图

前人通过试验和数值模拟的方法揭示了翼片式斜板沉沙池的泥沙沉降机理，对相关结构参数如翼片高度、翼片间距、翼片倾角等开展了单因素试验，定性分析了各因素对截除率的影响。由于影响截除率的因素较多，且各个影响因素对截除率的敏感性和显著性尚缺乏相应研究成果，实际工程应用时翼片式斜板沉沙池的结构优化过程缺乏依据。同时，由于前人对翼片式斜板沉沙池的截除率与各结构参数最优组合间的相关关系尚未开展系统研究，使其应用于工程实际时缺乏设计依据。因此，本文拟基于正交试验，通过极差分析得出影响截除率的敏感因素，借助方差分析法判断各因素对截除率影响的显著性。采用投影寻踪回归（PPR）方法建立稳定可靠的截除率与表面负荷、翼片高度及翼片间距的预测模型，获得各因素对截除率的贡献权重，和不同表面负荷时的截除率最优时的结构参数组合。研究成果可望为保证较高截除率时的翼片式沉沙池结构设计和优化提供依据和方法。

2 截除率正交试验简介

2.1 试验装置为了方便观察试验过程中的水流与颗粒运动的运动情况，本试验沉沙池采用透明有机玻璃制成，翼片式斜板采用黑色PVC塑料板制成。沉沙池主要尺寸及构成如图2所示。应用沉沙池池宽（D）对翼片间距和翼片高度进行无量纲化处理，试验中翼片间距分别为D/3、D/2、D/3，翼片高度分别为D/3、D/2、2D/3。翼片倾角分别取90°、75°、60°。

图2 翼片式斜板沉沙池模型系统试验布置图（单位：mm）

2.2 试验材料选择试验选用核桃沙作为模型沙进行试验。核桃沙粒径范围0.8～1.2 mm，堆积密度为0.81 t/m3。核桃沙呈黄褐色，能清晰地观察到其在沉沙池内及翼片槽内的运动轨迹，且易于被拦截不会再次进入循环系统。前人研究结果表明核桃沙属于轻质沙，其沉降特性与天然沙接近，使用核桃沙进行试验可以获得可靠的试验结果[7-8]。

2.3 试验方案试验选取翼片间距（A）、翼片倾角（B）、翼片高度（C）三个影响因素，每个因素下设计三个水平变量。本次试验所选因素及水平设计如表1所示。试验选用了三因素三水平试验方案，故正交表应选择L9（34），并将最后一列设为空列即误差列，以便方差分析。其试验方案见表2。

表1 试验因素及水平设计

表2 正交试验设计方案

笔者通过前期试验发现，在表面负荷小于16 m3/（h·m2）时翼片式斜板沉沙池截除率相比普通斜板沉沙池优势并不明显，且采用翼片式斜板反而会增加建设成本，故本试验选取输沙率为0.455 g/s、表面负荷分别为：16 m3/（h·m2），20 m3/（h·m2），24 m3/（h·m2），28 m3/（h·m2），32 m3/（h·m2）情况下进行截除率试验。

2.4 试验步骤图2为翼片式斜板沉沙池模型系统试验布置图。试验开始时从进水槽上方投放模型沙，在进流紊动作用下核桃沙与槽内水流充分混合，模型沙在沉沙池内以悬移运动为主，经翼片式斜板区域后，由出水挡板顶溢流入集水槽再经出水口流出。出水口下方放置回水箱，回水箱上方布置筛网（筛网孔径100目）拦截随水流溢出的模型沙，保证随水流溢出的模型沙不会再次进入沉沙池中。回水经进水管再次进入进水槽，实现整个系统的自循环。

3 试验结果分析

3.1 截除率的各影响因素敏感性与显著性分析对表2所列各方案下的翼片式斜板沉沙池截除率进行试验，每组试验结束后收集筛网上的核桃沙，用烘干机烘干后使用电子秤（精度为0.1 g）称其质量记为M1，加沙总质量记为M2，（M2-M1）/M2记为各组沉沙池的截除率。对试验所选用的各表面负荷下正交试验结果进行极差分析。因素的极差大小反应了该因素水平变动时，试验指标即截除率的变动幅度。极差越大说明该因素对截除率的影响也越大，故可以获得各因素敏感性及最优参数组合，结果见表3，表中Kij表示第i因素第j水平所对应的试验指标和的平均。从表中可以看出，各试验工况下空列的极差值均小于其他因素的极差，表明在试验过程中试验误差对截除率影响小于其他三项，即该组试验数据有效，可进行方差分析，继而获得翼片间距、倾角、高度对截除率的影响。

由表3还可知，在表面负荷16 m3/（h·m2）、20 m3/（h·m2）、24 m3/（h·m2）时三者极差分析结果一致。表面负荷一定的情况下，因素翼片间距（A）极差最大，其次是翼片高度（C），最后是翼片倾角（B）。截除率对各因素敏感性由大到小为A-C-B，即表面负荷16 m3/（h·m2）、20 m3/（h·m2）、24 m3/（h·m2）时翼片间距（A）对截除率起着主要影响作用，翼片式斜板最优结构组合为翼片间距取D/2，翼片倾角取60°，翼片高度取D/2。

表面负荷28m3/（h·m2）及32 m3/（h·m2）时两者极差分析结果一致。因素翼片高度（C）极差最大，其次是翼片间距（A），最后是翼片倾角（B）。截除率对各因素敏感性由大到小为C-A-B。翼片式斜板最优结构组合为翼片间距取D/3，翼片倾角取90°，翼片高度D/2。

为了更加直观的分析各因素对截除率的影响，根据表3可做出各因素对截除率影响的直观分析图，如图3所示。从图中可以看出，表面负荷16 m3/（h·m2）、20 m3/（h·m2）、24 m3/（h·m2）时截除率随着翼片间距、翼片高度的增大先增大后减小，随着翼片倾角倾斜程度的增加而增加，且随着翼片间距的变化最为明显，即截除率对翼片间距最为敏感。28 m3/（h·m2）及32 m3/（h·m2）时，截除率随着翼片间距的增大而减小，随着翼片夹角倾角的变大而减小，随着翼片高度的增加截除率呈现先增大后急剧变小的趋势。翼片高度对截除率的变化影响最大，即截除率对翼片高度最为敏感。

表3 截除率极差分析结果

图3 截除率影响因素直观图

为了得到各因素对截除率的影响程度是否显著，对正交试验结果进行方差分析，在方差分析中将因素的显著性水平划分为四个等级（1）当F≥F0.01为高度显著影响，记为“***”，（2）当F0.01＞F≥F0.05为显著影响，记为“**”，（3）当F0.05＞F≥F0.1为影响不十分显著，记为“*”，（4）当F＜F0.1为无显著影响，记为“×”。分析结果见表4。由表4可以看出表面负荷16 m3/（h·m2）时翼片间距为显著影响因素，倾角、高度为无显著影响因素。20 m3/（h·m2）时翼片间距为显著影响因素，高度为不十分显著因素，倾角为无显著影响因素。24 m3/（h·m2）时翼片间距为不十分显著因素，倾角、高度为无显著影响因素。28 m3/（h·m2）时翼片高度为显著影响因素，间距、倾角为无显著影响因素。32 m3/（h·m2）时翼片高度为高度显著影响因素，间距为不十分显著因素，倾角为无显著影响因素。

3.2 基于投影寻踪回归模型（PPR）的截除率仿真计算及分析投影寻踪回归的原理是将试验得到的高维数据利用计算机将其投影到低维子空间上，借此实现“高维数据低维化”的目的，通过对低维子空间数据的分析，找出能够反映高维原始数据内部特征的非正态信息和规律并进行回归分析，从而实现对高维数据的分析[9]。PPR模型表达方式及详细计算方法可见参考文献[10-11]，此处不再赘述。

通过上文正交试验结果极差分析和方差分析可以看出，影响截除率的主要因素为翼片间距与翼片高度，翼片倾角是非显著性因素，为提高运算效率及精度在使用PPR建模时不考虑翼片倾角，而是将翼片间距、翼片高度、表面负荷作为建模参数。除45组建模样本外，事先预留了18组检验样本。稳定性分析时首先采用PPR程序对建模样本进行建模运算，并基于此模型对建模样本进行“还原拟合”计算，取“还原拟合”值与建模样本实测值做差，一般相对误差|δ|＜10%作为合格率判断标准[12]，借此确定模型的合格率。之后将预留检验样本数据带入PPR模型，计算预留检验样本合格率，当其也满足合格标准时，认为此PPR模型具有较好的稳定性与可靠度。

采用郑祖国等[13-14]自主开发的PPR程序对翼片式斜板沉沙池截除率进行建模分析。运行时指定5个投影参数分别为：P=3，Q=1，S=0.1，M=5，Mu=3。其中P为影响因素个数；Q为因变量个数；S为光滑系数，决定了模型的灵敏度，S越小则模型越灵敏，取值范围为0＜S＜1；M为岭函数上限个数；Mu为岭函数最优个数。M与Mu决定了模型寻找数据内在结构的精密程度。通过PPR建模运算可得到模型的投影方向如式（1）所列，模型所需岭函数如图4所示。同时可得到相应岭函数的权重系数β如式（2）所示。

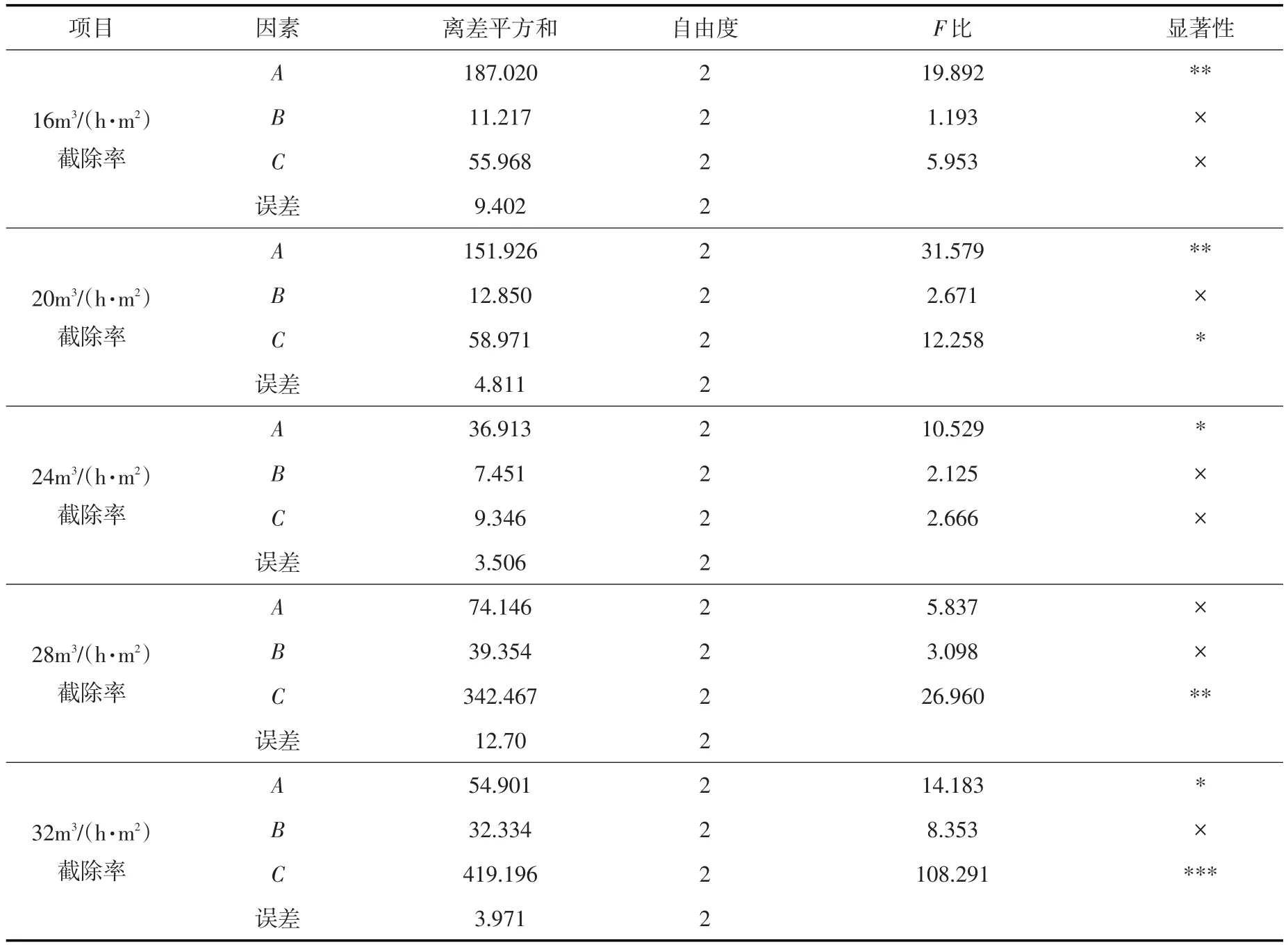
表4 截除率方差分析结果

图4 翼片式斜板沉沙池截除率PPR模型岭函数图

此外，用PPR程序对翼片式斜板沉沙池截除率进行计算，得到各影响因子对翼片式沉沙池截除率贡献权重系数为：表面负荷=1，翼片间距=0.686，翼片高度=0.527。

依据上述PPR建模过程，对截除率建模样本与其预留检验样本进行预测，并与实测值进行比较，如图5所示。由图5可知，建模样本与检验样本的截除率预测值与实测值偏差较小，当相对误差|δ|＜6%时，建模样本与检验样本的合格率均为100%，当相对误差|δ|＜5%时建模样本与检验样本的合格率分别为93.33%和94.44%，平均相对误差分别为2.03%和1.92%。表明PPR模型具有较好的可靠性，故可根据此模型对未进行试验的工况进行预测，分析各种工况下翼片式斜板沉沙池的最优结构参数组合，为实际应用提供参考。

例如，借助此模型分别对表面负荷取16，17，…，31，32 m3（/h·m2）；翼片间距分别取A/D为0.333，0.417，0.5，0.583，0.667；翼片高度分别取C/D为0.33，0.417，0.5，0.5833，0.667时的不同试验组合进行仿真运算。因数据较多，以表面负荷22 m3（/h·m2）与30 m3（/h·m2）为例，绘制翼片间距（A）/池宽（D）与翼片高度（C）/池宽（D）对截除率影响的等值线图即图6。通过等值线图可以直观的观察到在某一表面负荷下翼片式斜板最优的间距及高度组合情况。由图6可以看出，不同表面负荷下截除率都随着翼片间距占比的增加呈现先增加后减小的趋势，最优区间在翼片间距占池宽0.5～0.6附近，不同表面负荷下截除率也随着翼片高度占比的增加呈现先增加后减小的趋势，最优区间在翼片高度占池宽0.5附近。

图5 截除率PPR建模计算精度分析

图6 截除率与A/D、C/D的关系

4 结论

选用模型沙（核桃沙），基于正交试验在多种表面负荷下对不同结构参数的翼片式斜板沉沙池的截除率进行了系统试验，采用极差分析法与方差分析法对试验结果进行敏感性与显著性分析，并建立了有较好可靠性的PPR运算模型，借助此模型对未能进行试验的工况进行预测，主要得到以下结论：

（1）不同表面负荷下，截除率的敏感因素与显著性因素是不同的。在表面负荷小于等于24 m3/（h·m2）时，截除率的敏感因素是翼片间距，主要显著性因素也为翼片间距。当表面负荷大于24 m3/（h·m2）时，截除率的敏感性因素为翼片高度，主要显著性因素也为翼片高度。翼片倾角不是截除率的敏感因素与显著性因素。

（2）结合敏感性分析、显著性分析及PPR仿真计算分析，可知在表面负荷16～32 m3/（h·m2）范围内时，翼片间距与池宽的比值取0.35～0.55时截除率较优，翼片高度与池宽的比值取0.45～0.55时截除率较优，翼片倾角在表面负荷小于等于24 m3/（h·m2）时可取60°，表面负荷大于24 m3/（h·m2）可取90°。

（3）将PPR程序用于翼片式斜板沉沙池截除率高维建模中，建立了稳定可靠的计算模型，能够客观的挖掘翼片式斜板沉沙池截除率高维数据内在的本质结构，确定各影响因子对截除率贡献权重系数由大到小为：表面负荷，翼片间距，翼片高度。所采用的方法能对不同结构参数的翼片式斜板截除率进行预测且有着较好的可靠性，可以给出不同表面负荷下截除率最优结构参数建议，为生产设计提供理论支撑。