电动汽车无线充电系统原边和副边整流桥的无源控制
2020-12-04杨金明孙杰杉刘润鹏
杨金明 孙杰杉 刘润鹏
(华南理工大学 电力学院,广东 广州 510640)
随着电动汽车的日益普及,续航能力问题已成为阻碍电动汽车进一步发展的瓶颈。在这种情况下,电动汽车无线电能传输技术受到了越来越多的关注[1- 4]。比起传统的插拔式充电方式,无线充电方式不但更为便捷,还能在电动汽车行进过程中进行充电[5- 9]。这种动态无线充电方式可以减少电池容量对于电动汽车发展的限制,有利于电动汽车的进一步推广。
动态无线电能传输系统的基本实现方式是先从电网取出交流电能,电能经整流装置变为直流后,再经由高频逆变装置逆变为高频交流电,交流频率一般在几十千赫兹到几百千赫兹之间[10- 12]。高频电流经过原边补偿电路后流过原边线圈,由于原边和副边线圈间存在互感,副边线圈产生感应电压,所产生的电能经过副边补偿电路后再经整流桥变为直流电,供给负载。文献[13]中研究了基于多发射线圈的动态无线电能传输系统的原边检测方法,文献[14]中提出了一种控制副边DC-DC电路的无源控制方法,文献[15]中研究了基于原边信息估计副边、再进行移相控制的控制策略。以上研究分别从原边和副边角度对动态无线电能传输系统进行了分析和控制,具有一定的应用价值,但对原边和副边整流部分则关注较少,一般是从原边直流电源开始分析,同时将副边整流桥和负载电路看作纯负载,并忽略功率因数校正电路。事实上,这种等效存在一定误差。此外,目前研究者们也鲜少关注无线充电装置对电网的影响。
动态无线电能传输系统整流桥具有强非线性,且汽车行进过程中存在实时的参数变化,使得相关的控制难度较高。无源控制是一种基于能量的视角、通过全局定义并实现全局稳定的控制方法,因此,可考虑基于无源控制算法并结合系统的具体特点,探索电动汽车无线充电系统双边整流桥的控制策略。鉴于此,文中拟构建原边和副边整流桥的欧拉-拉格朗日(Euler-Lagrange,EL)模型,结合动态无线电能传输系统的特点,设计原边和副边整流桥的无源控制的控制律,实现在互感和负载波动情况下的功率因数校正和恒压输出。
1 控制目标与原边、副边整流桥E-L模型
1.1 控制目标
常见的动态无线电能传输系统的基本结构如图1所示,发射线圈沿电动汽车行进道路铺设,接收线圈置于电动汽车底部。一般只有位于电动汽车正下方的两个发射线圈导通,其他线圈不导通,使空载损耗尽量小,所以只需分析原边的两个发射线圈和副边的一个接收线圈的互感关系。

图1 动态无线电能传输系统结构图
系统从直流端到负载的电路连接如图2所示。动态无线电能传输系统常使用LCC-S补偿结构,该拓扑结构的特点是原边发射线圈电流的大小只与输入电压和原边补偿结构的参数有关[16],不受互感和负载波动的影响,使得原边和副边可以分开分析。
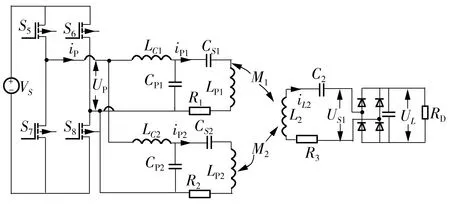
UP和iP为逆变桥的输出电压和输出电流,US1为整流桥 的输入电压,其他符号代表的物理量见下文述及
通过采用LCC-S补偿拓扑结构,只要原边输入电压和补偿结构参数不变,原边发射线圈电流iP1和iP2就始终相等,满足iP1=iP2=iP。此时副边接收线圈上耦合产生的电压U2表示为
U2=jω(M1+M2)iP
(1)
通过优化发射和接收线圈的结构参数及空间布置,可以使得M1+M2的波动尽量小;但考虑到总体成本,M1+M2的波动无法完全消除,使得耦合电压U2会在电动汽车行进过程中产生波动,造成负载电压不稳定。
此外,由于副边整流桥输出端滤波电容的存在,副边整流桥只有在输入电压大于输出滤波电容电压的情况下才能输出电能,造成电流的波形畸变,使副边产生一定量的谐波,影响传输效率。因此,需要进行功率因数校正,使副边整流桥的输出为纯阻性。副边整流桥的控制目标是在互感和负载波动情况下实现整流桥的恒定电压输出,同时实现整流桥输入电压和电流的功率因数校正。
与副边整流桥类似,原边整流桥由于一边连接电网,一边连接波动的负载,也需要保证恒定的电压输出和功率因数校正,以确保动态无线电能传输系统稳定的供电以及尽可能少的谐波流入电网。下文将结合动态无线电能传输系统的特点,设计能实现上述目标的原边和副边整流桥无源控制的控制律。
1.2 副边整流桥的E-L模型
在动态无线电能传输系统中,由于线圈间互感的改变,副边感应电压U2为一不确定值,在某一范围内波动。副边电路连接如图3所示。

RD为整流桥及其负载的等效电阻,整流桥采用全控整流
根据图3,在S1和S4导通、S2和S3导通两种情况下列出各变量间的方程,具体如下:
S1和S4导通时,有
(2)
S2和S3导通时,有
(3)
通过状态空间平均的方法,所列方程组可改写成如下形式:
(4)
式中,LSS为原边整流桥的续流电感,VC2为C2上的电压,VCSS为CSS上的电压,CSS为滤波电容,Io为流过负载RD的电流。S=1表示开关S1和S4导通,S2和S3关断;S=-1表示开关S1和S4关断,S2和S3导通。S与开关管控制脉冲的占空比D的关系满足:
(5)
(6)
D表示一个周期T内S1和S4导通占整个周期的比例,控制S1、S4导通的信号与控制S2、S3导通的信号互补。
取状态变量为x1=iL2、x2=VC2、x3=VCSS,将式(4)改写成E-L方程的形式:
(7)
即

(8)
由于忽略了整流桥和电容电感上的损耗,故略去反应系统耗散特性的RX项。式(8)中,X为系统的状态变量,
X=[x1x2x3]T
(9)
M为正定的对角矩阵,
(10)
J为反对称矩阵,反映系统内部的互联关系,

(11)
此外,
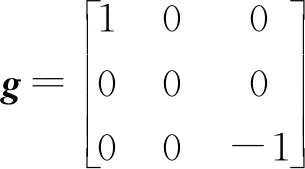
(12)
u=[U20Io]T
(13)
g和u相乘表示系统和外部的能量交换。
1.3 原边整流桥的E-L模型
原边整流桥电路及系统其他部分的示意图如图4所示。

Vg为输入的50 Hz交流电压,LS为输入滤波电感, Ig为整流桥输入电流,Io1为整流桥输出电流
与副边整流桥类似,列出原边整流桥各变量的关系式如下:
(14)
取状态变量为y1=Ig,y2=VCS,Y=[y1y2]T,将式(14)改写成E-L方程的形式:
(15)
2 系统无源控制设计
2.1 副边整流桥无源控制设计
在副边整流桥E-L模型基础上,根据无源性定义,系统(8)是严格无源的。定义系统变量目标整定值
(16)
系统的状态误差向量
xe=X-X*
(17)
将其代入式(8),得到副边整流桥的误差状态模型如下:
(18)
误差能量函数为
(19)
求取导数,得
(20)
令
(21)
得到无源控制律
(22)
其中
(23)
为系统注入阻尼项,r1、r2、r3为向系统注入的阻尼,其作用为加快系统的收敛速度。从式(22)可推出控制律如下:
(24)
由于电动汽车行进过程中互感的实时值未知,电感上的耦合电压U2不能采样得到,因此使用Ui来代替U2,将式(24)改写成以下形式:
(25)
即
(26)
其中Ui与U2的关系为
(27)
易知,Ui是可测量的。
(28)
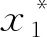
(29)
虽然式(26)中用Ui代替了U2,但Ui和U2只有在一个周期内才满足式(27),因此在式(29)中无法用Uimax来代替U2max。此时通过前文的分析可知,采用双发射线圈,发射和接收线圈之间的互感值在汽车行进过程中只在小范围波动,故耦合电压的幅值U2max也在小范围波动,由此可以计算出耦合电压幅值的平均值U2max-ref,再引入整流输出电压负反馈,通过PI模块对互感波动下的耦合电压幅值的真实值进行追踪,可使得耦合电压幅值变为U2max=U2max-ref+ΔU2max,进而,状态量x1的期望点表示为
(30)
耦合电压幅值追踪的PI模块如图5所示。
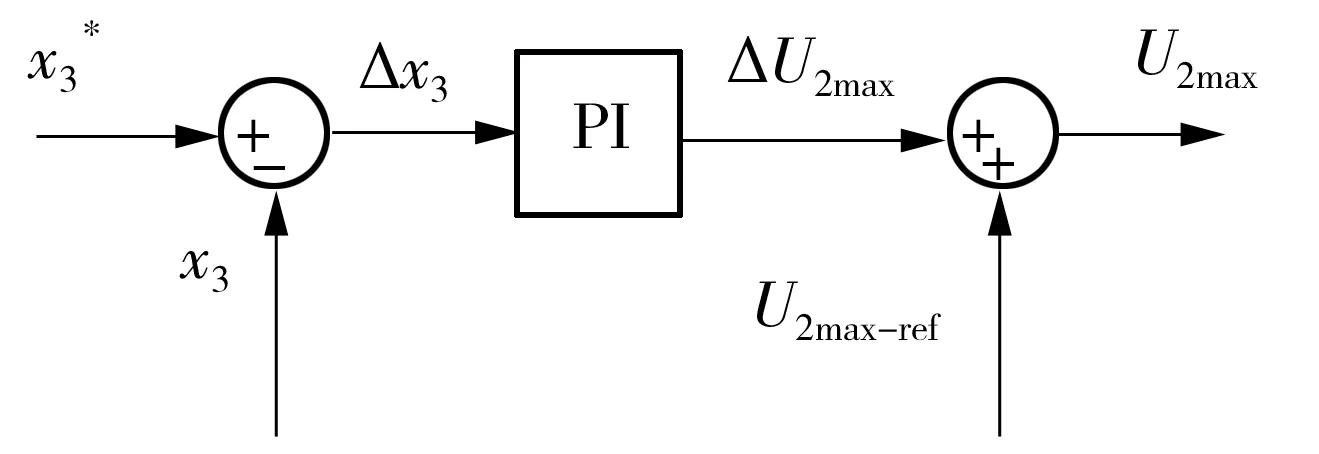
图5 副边感应电压基准值的校正模块
在实际中,动态无线电能传输系统的原边、副边互感值一般在小范围内波动(波动幅度一般小于20%),因此可以基于互感平均值算出耦合电压峰值的平均值,在此平均值基础上确定波动范围,通过PI追踪x1的整定值。
综上可得无线充电系统副边整流控制结构,如图6所示。

图6 副边整流桥控制示意图
2.2 原边整流桥无源控制设计
与副边整流桥无源控制设计类似,令
ye=Y-Y*
(31)
将其代入式(8)并计算,得到无源控制律
(32)
其中
(33)
为系统注入阻尼项,ζ1、ζ2为向系统注入的阻尼,根据式(32)可以推出控制律如下:
(34)

(35)

(36)
其中传输到负载的功率Pout表示为
(37)

(38)
3 仿真验证
3.1 副边无源控制仿真
在Simulink中搭建从高频交流源到副边负载的仿真模型,其中交流源电压峰值为60 V,频率为100 kHz,电路参数列于表1,参数符号与图2对应。

表1 副边系统建模参数Table 1 Modeling parameters of secondary system
原边、副边线圈互感为6.5 μH、负载为25 Ω时,得到电源电压VS和流过接收线圈的电流ILSS的波形,如图7所示。图8示出了整流桥的输出电压波形。在0.4 ms时,VS与ILSS实现了同相位。由前文分析知VS和副边感应电压U2同相位,可知整流桥实现了功率因数校正。

图7 M=6.5 μH时整流桥的输入电流与电源电压波形

图8 M=6.5 μH时整流桥的输出电压波形
当发射线圈和接收线圈间的互感原为7.5 μH,在0.01 s变为6 μH,负载仍为25 Ω时,电源电压VS和电流ILSS在变化时刻附近的波形如图9所示,整流桥的输出电压波形如图10所示。由图可知,在互感变化时整流桥仍实现了功率因数校正和目标电压输出。
当发射线圈和接收线圈之间的互感为5.5 μH,负载在0.013 s时由25 Ω变成30 Ω,0.027 s时由30 Ω变成35 Ω时,整流桥的输出电压波形如图11所示,输出功率如图12所示。由图可知,在互感偏离平均值且负载波动时,整流桥可保证目标电压的恒定输出。

图9 互感波动时整流桥的输入电流与电源电压波形

图10 互感波动时整流桥的输出电压波形

图11 互感为5.5 μH、负载波动时整流桥的输出电压波形
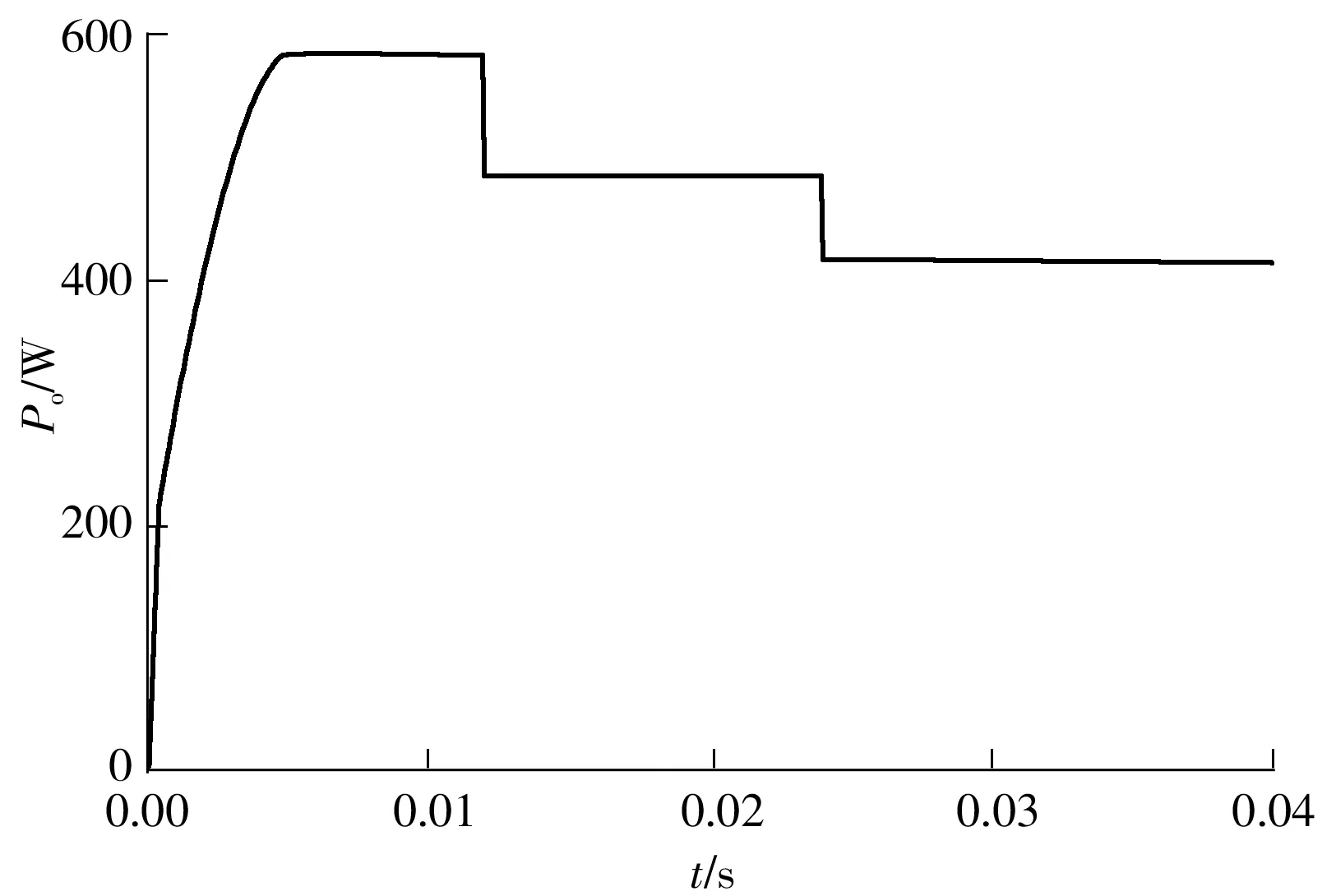
图12 互感为5.5 μH、负载波动时整流桥的输出功率折线图
3.2 原边、副边无源控制联合仿真
在Simulink中搭建原边整流桥仿真模型,与逆变桥串联后代替3.1节中的原边交流电源,电路连接如图4所示。其中输入50 Hz交流源的电压峰值为45 V,电路参数如表2所示,表中参数符号与图4对应。

表2 原边系统建模参数Table 2 Modeling parameters of primary system
当互感在0.1 s由6.5 μH变为5.5 μH,负载在0.2 s由30 Ω变为25 Ω时,原边整流桥的输入电压和电流波形如图13所示,负载输出电压波形如图14所示,负载功率波形如图15所示。由图可知,整个系统实现了功率因数校正,且保持恒压输出,当互感和负载发生波动时,输出电压始终为80 V。

图13 互感和负载变化时的原边输入电流与电压波形
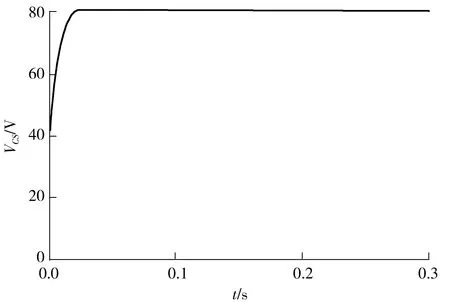
图14 互感和负载变化时的负载电压波形
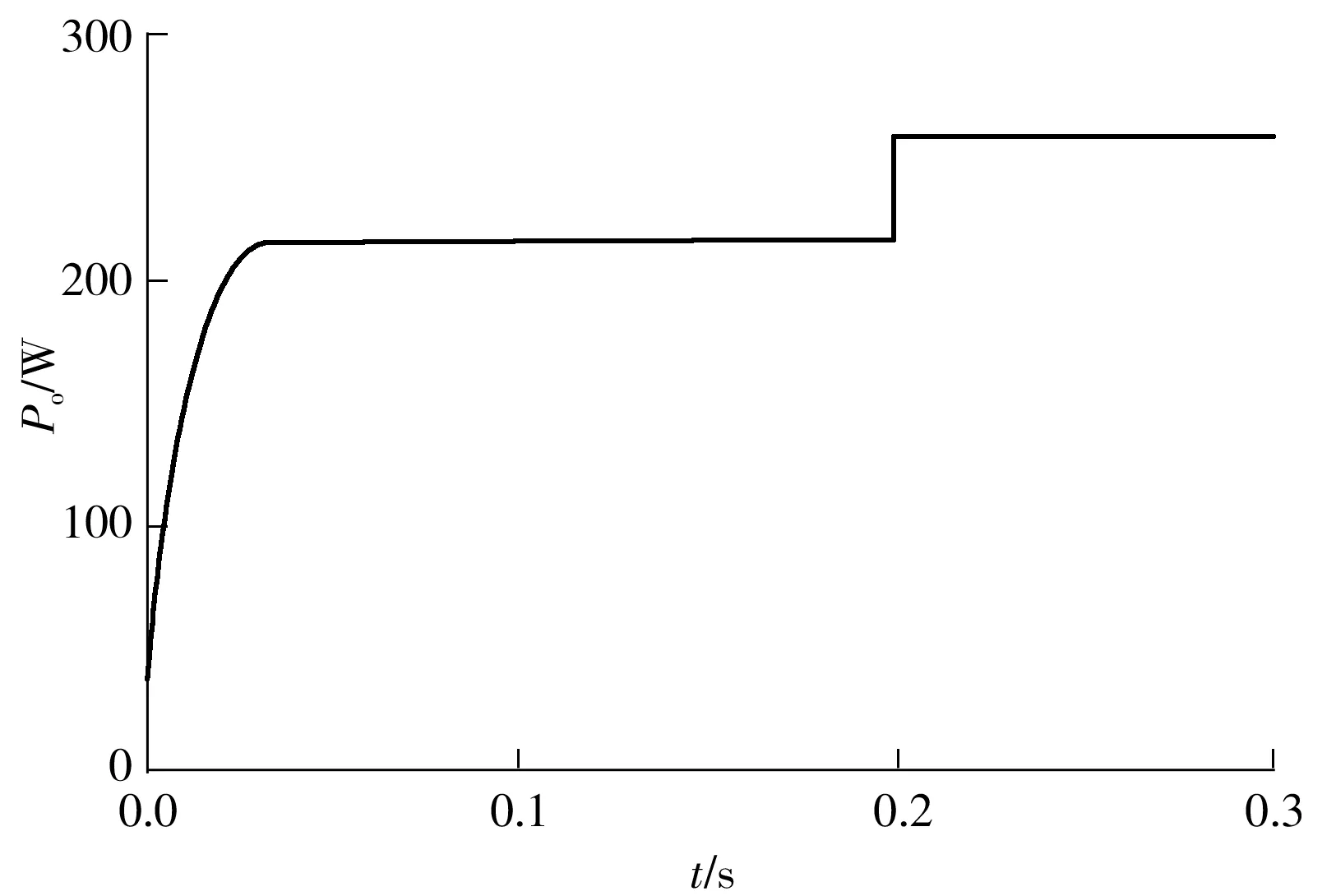
图15 互感和负载变化时的输出功率波形
由图13和14可知,系统在0.1 s的互感变化和0.2 s的负载变化下都能够实现功率因数校正和恒压输出,输出功率在互感波动时没有变化,在负载波动时相应改变。由此可知系统在负载波动情况下能够较为迅速地实现功率因数校正和稳定的输出电压控制。
4 实验验证
系统副边主电路为100 kHz高频电路,受实验条件限制,暂时无法做出对应实验,故只搭建原边整流桥实验平台,验证所提出的无源控制算法的可行性。所搭建的原边整流桥实验装置如图16所示,各元件的参数如表3所示。首先通过调压器将市电降压为峰值15 V的50 Hz交流电,经过滤波电感后与整流桥相连。整流桥输出端接一电阻负载,代表动态无线电能传输系统的用电。

表3 实验参数表Table 3 Parameters of experiment
实验通过电压和电流采样电路采集到电压电流信号后,输入DSP28335运算,运算得到的控制信号输出给整流桥驱动电路,驱动整流桥MOSFET开关管的开通和关断。设定目标输出电压为20 V,负载从50 Ω变成70 Ω。
电路接通并开启DSP后,输出电压和输出电流的波形如图17所示;当负载波动时,输出电压的变化如图18所示。

图16 实验装置图Fig.16 Experimental device
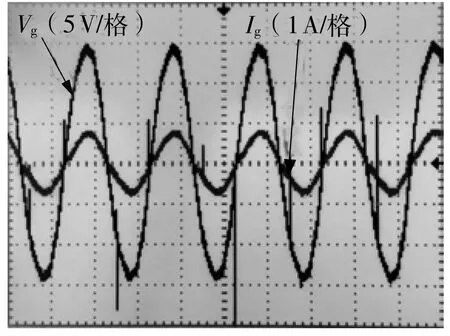
图17 整流桥的输入电压和电流波形截屏
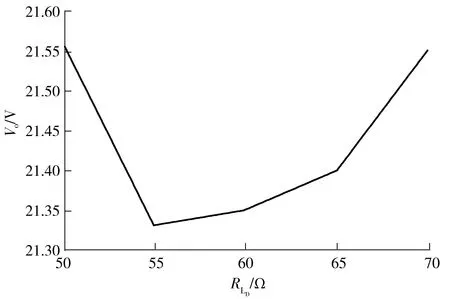
图18 整流桥的输出电压折线图Fig.18 Output voltage line diagram of rectifier bridge
由图17可知,整流桥的输出电压和电流处于同一相位,通过无源控制实现了输入端的功率因数校正,且从图18所示的输出电压折线图可知,当负载波动时,输出电压偏离目标电压(20 V)最多不超过1.6 V,实现了较为稳定的电压输出。
5 结语
文中推导了动态无线电能传输系统原边和副边整流桥的E-L模型,根据系统特点设计了相应的控制律,仿真和实验表明,所推导的原边和副边整流桥E-L模型方程和使用PI追踪整定值的无源控制算法可以迅速、稳定地实现原边和副边整流桥的功率因数校正和恒压输出。
文中还通过具体实验,初步验证了所设计的无源控制算法的可实现性。由于条件限制,没有通过实验来验证副边整流桥的无源控制算法,这将在之后的研究中进一步探索。
