测量仪器快速整平对中原理及方法研究

陈文生

（郑州铁路科技发展有限公司，河南 郑州 450000）

各种工程对测量的精度要求越来越高，仪器高的量取是测绘外业中的首要程序，仪器高的精度决定了测量外业的整体精度。仪器高，是指仪器度盘中心到测站点的铅垂距离。目前量取仪器高的通用方法是钢尺量距法，其理论精度约为2～3mm[1]，实际操作中在各种因素的影响下其精度会更低，这在精密工程测量中是一个不能回避的问题，如何设法提高仪器高的量取精度是一个很重要的基础问题[2]。整平和对中是测量中的基础工作，整平是使仪器竖轴为铅垂线状态，使其水平度盘为水平状态；对中是使仪器中心与对中点在同一铅垂线上[3]。在工程测量中，由于不清楚整平和对中的原理，导致在实际操作中盲目而又不得法，浪费了大量的时间精力。通过实践发现，先使仪器中心与对中点重合，在仪器大致水平的情况下，通过调节三脚架进行整平时仪器中心与对中点并没有明显分离，有人称之为三脚架的指心现象[4-6]。文章对这一现象进行研究，总结出一套实用的仪器快速整平对中方法，为相关工作人员提供实际的工作参考。

1 快速整平对中方法

1.1 精对中粗整平

安置仪器后，移动三脚架，并注意观察以光学对中器或对中激光点为代表的仪器中心，通过移动使仪器中心与对中点重合，在这个过程中保证仪器大致水平。

1.2 精整平

根据水准气泡位置，调节对应的脚架，操作方法为沿脚架中心线在地面上的投影线上前后移动脚架或选择伸缩脚架。在坚硬地面选择直接移动脚架较快捷，在松软地面将脚架踩实后进行伸缩较快捷，也可以二者同时进行，直至水准气泡居中。

1.3 精对中精整平

基于三脚架的指心现象，此时仪器中心与对中点并没有明显的偏移，但由于操作上的误差等原因可能导致一定范围内的偏移。此时通过调节仪器微动螺旋使其水平，并通过移动仪器使其精确对中即可。

2 三脚架指心现象的证明

2.1 脚架操作

对脚架的操作主要包括两种：（1）脚架在地面点位置不变，伸缩某一脚架；（2）沿脚架在地面的投影线方向移动某一脚架。

2.2 脚架体分析

脚架体由三个脚架及上平面组成，三脚架实物图见图1。可以将脚架简化为A、B、C三条线段，见图2（a），固定脚架A、B，只研究脚架C活动时的影响，此时AB为一个整体，将其简化，见图2（b）。实践发现，当活动其中一个脚架时，脚架上平面和另外两个脚架组成的架构是不变的。

图1 三脚架实物图

2.3 脚架整平及对中模型研究

脚架整平及对中的实质可以认为是脚架上平面的几何中心O处垂线的延长线与对中点P相交，见图3（a）。在脚架C方向进行整平，其他方向本质与此相同，由于脚架操作法的限制条件，脚架移动时，AB-O总是一起活动，又根据AB-O在脚架活动过程中是不变形的，因此脚架整平可以看作以AB与地面的交点为旋转点进行顺时针旋转直至上平面水平为止，此时水准气泡居中。假设在理想情况下脚架上平面达到水平位置，见图3（b），需要研究在这个过程中仪器中心偏离对中点的程度。

进一步发现图3（b）状态时的结构组成平面四边形，见图4（a），操作过程相当于以脚架旋转点为中心的几何旋转。图4（a）中α为固定角度，ε为脚架上平面不平行引起的夹角，此时对中垂线与地面的交点设为P′，见图4（b），P′偏移对中点P的距离设为R，脚架旋转点到对中点P的距离设为L。由图4（a）得知R=L-L×cosε，在实际情况下，脚架距对中点的距离L≤0.5m。在仪器粗平的情况下，ε一般小于10°，由此进行计算得R≤7mm。而在一般情况下，R远小于这个数值，可以认为在脚架整平过程中，仪器中心在对中点的投影几乎没有偏移，这就证明了三脚架的指心现象。

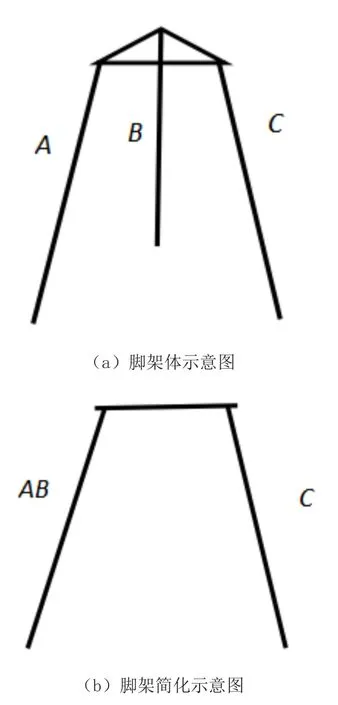
图2 脚架体分析图

图3 脚架活动示意图

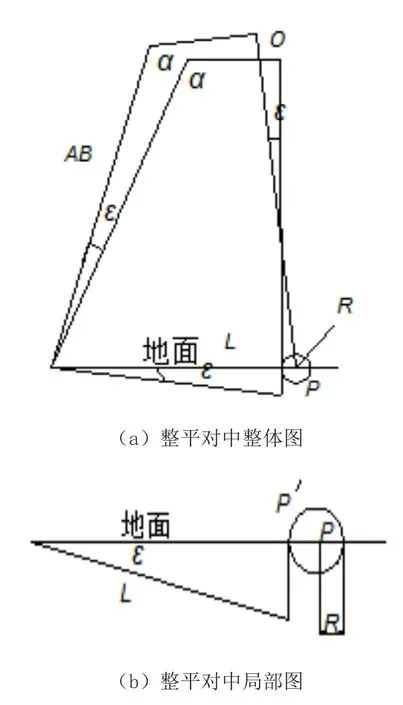
图4 整平对中结构分析图

3 结束语

在实际的操作中发现，当移动脚架C时全站仪对中点处的激光会在其周围小范围移动，其原因是在实际操作中，不可能精确保证AB-O在同一平面活动，从而导致仪器中心的偏移，所以本方法的要点就在于操作时要注意脚架的正确移动。文章用几何方法证明了三脚架指心现象，进一步说明了仪器整平对中是可以分开进行的事实，提出的整平对中方法也能快速地应用于实际工作中。