降低起点 拉长过程 人人得法——《鸡兔同笼》教学实录与思考

金雪凤

【教学内容】

人教版四年级下册数学广角《鸡兔同笼》单元第一课时。

【教学重点】

初步掌握用列举的方法解决问题。

【教学难点】

尝试用“一次或少量调整”的方法解决问题，理解推理过程。

【教学过程】

一、尝试列举，发现规律

1.呈现情境，教会列举方法。

师：今天这节课我们一起来解决一些有趣的数学问题！

出示学习材料（图1），解读信息。

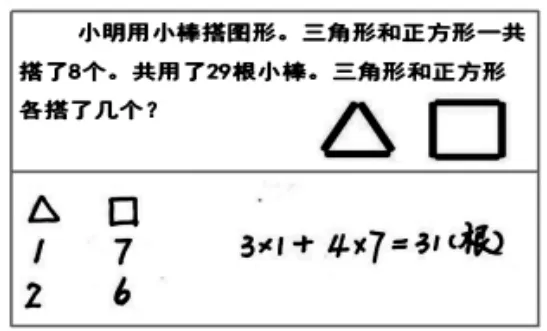
图1

师：这样的问题你会解决吗？

（个别学生举手表示可以用画图、假设、列举法等来解决）

师：像这样的问题解决的方法有很多，今天这节课我们一起用列举的方法来解决。你打算怎么列举？

生：先想1 个三角形，7 个正方形，算算要用几根小棒，如果小棒根数不对，就再换一个试试。

（教师板书学生方法，师生共同计算小棒根数）

师：1 个三角形，7 个正方形是31 根小棒，这个不符合要求。那接下去你打算怎么列举呢？

生：2 个三角形，6 个正方形。

师：你怎么想的？

生：小明搭了8 个图形，三角形2 个，那么正方形就是6 个。

师：你的意思是三角形个数与正方形个数加起来必须是8个。你们会接下去列举吗？

（自主列举，解决问题）

2.核心问题，引领发现规律。

师：小王同学是这样列举的（如图2），谁看懂了？

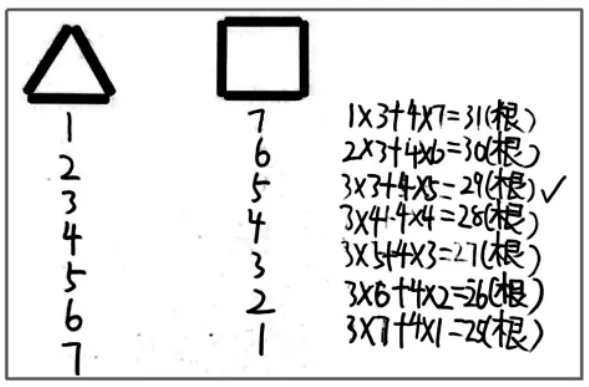
图2

生：他是从1 个三角形，7 个正方形开始，一个一个有序列出来的。正确答案是3 个三角形，5个正方形。

师：小张同学是这样列举的（如图3），你同意吗？和你的同桌说说你的想法。

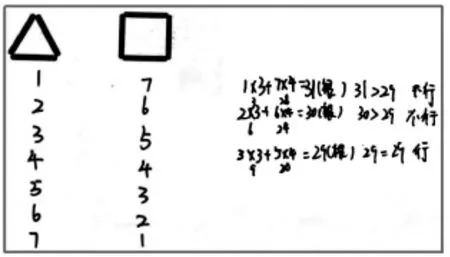
图3

生：我认为这样不可以，他没有列完整，万一后面还有符合要求的答案呢。

生：我觉得这样可以的，因为后面没有正确答案了。列下去也是浪费时间。

师：你怎么知道后面肯定没有符合要求的答案了？

生：三角形每次多1 个，正方形每次少一个，小棒的总根数就会少1 根。列到三角形3 个，正方形5 个时，后面的小棒根数会比29 根更少，肯定不符合要求，所以不用列下去了。

师：为什么这里小棒根数每次会少1？

生：搭一个三角形比搭一个正方形少用一根小棒，所以三角形个数多一个，正方形个数少一个，总根数就会少一根。

师：看来，找到一个正确答案后可以不列下去了。

二、巩固列举，把握规律

出示任务二（如图4），解读信息，自主尝试。

图4

展示典型作品一（如图5）。

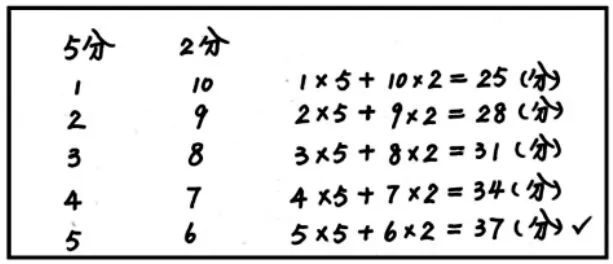
图5

师：谁和他的想法是一样的？为什么列到5 枚5 分，6 枚2 分就不用列下去了呢？

生：因为每次多一枚5 分，少一枚2 分，总的钱数就增加3 分。每次加3 分，37 分下面应该是40分了，后面还会越来越多。

师：如果我们从1 枚2 分，10枚5 分开始想，可以吗？

（学生齐答可以）

展示作品二（如图6）。

图6

生：我觉得他很会动脑筋。他发现每次增加一枚5 分，减少一枚2 分，总钱数就增加3 分，他就直接3 分3 分地加上去，一直加到37 分，就知道答案是几了。

师：很好，你很会欣赏别人的优点。这位同学根据规律直接写出总钱数，让列举的过程简单了很多。

展示作品三（如图7）。

图7

师：你是怎么想的？

生：我是跳着想的。我先想1枚5 分、10 枚2 分，这样总面值少很多。再想3 枚5 分、8 枚2分，这样加起来是31 分。再把5分的变成5 枚，2 分的变成6 枚，总面值刚好是37 分。

小结：通过刚才的交流，我们发现列举时可以一一有序列举，也可以跳着列举。

三、灵活列举，运用规律

出示任务三（如图8），解读信息。

图8

师：这个问题你打算怎么列举呢？比比谁更快地想到答案。

自主尝试后组织交流。呈现不同的列举方法（如图9、图10），引导思考：这样列举你能看懂吗？

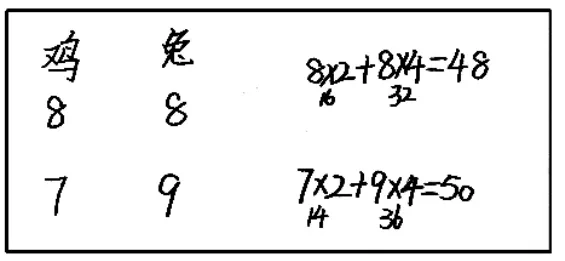
图9

图10

生：图9 是从中间列举的，8只鸡，8 只兔，共48 条腿，还少了2 条腿。因为一只兔比一只鸡多两条腿，所以减少一只鸡，增加一只兔，腿增加两条。

师：是呀，我们不仅可以从两头列举，也可以从中间列举。

生：图10 从1 只鸡，15 只兔开始列举，共62 条腿，多了12条腿。一只兔比一只鸡多两条腿，所以增加一只鸡，减少一只兔，腿减少两条，调整为7 只鸡9只兔。

师：你真厉害，根据规律调整一次就找到正确答案了。

师：如果我从0 只鸡，16 只兔开始想，可以吗？

（只问不要求学生回答）

四、反思求联，初建模型

师：今天我们用列举法解决了三个问题，这三个问题有什么相同之处？

生：都是鸡兔同笼类的题目。

师：你怎么知道这些都是鸡兔同笼类的题目？

生：第一题三角形和正方形相当于是鸡和兔，8 个图形相当于就是8 个头，29 根小棒相当于29 条腿。第二题5 分硬币、2 分硬币相当于是鸡和兔，11 枚硬币相当于就是11 个头，37 分相当于是37 条腿。

师：你分析得很有道理，所以这些问题我们可以称为“鸡兔同笼”类问题，今天我们采用的是列举的方法，下一节课我们学习用其他方法解决。

【课后思考】

“鸡兔同笼”是我国古代数学的经典趣题，重在培养学生的数学思维能力。解决“鸡兔同笼”问题的方法有很多，如“画图、列举、假设、方程”等，每种方法都有各自的教学价值。对于初接触此类问题的学生来说，列举法无疑是最自然的方法。本课以“鸡兔同笼”问题为载体，教学最能被广泛迁移的列举法。给予学生充分的感悟时间，丰富体验，为“假设法”的产生与理解奠定基础。有效促进学生面对陌生问题时形成“先试试看”的思维方式和勇于尝试的思维品质。针对不同学生的差异，开放性组织反馈交流活动，充分展示学生个性化思路，给予不同层次学生增量发展的空间，让后进生在鸡兔同笼这样的“高阶思维”课程中不再扮演“陪跑”“观众”的角色，而同样成为赛场的“正式选手”。

“鸡兔同笼”问题的价值不是解题的技巧，而是借助其趣味性提升学生的思维深度，领悟其中蕴含的数学思想方法。本课基于目标定位，以生为本，重组材料，重构课堂，关注群体背后的个体，着眼结果背后的过程，让学生的数学思维得到生长。