尊重知识起点 修正学生经验——《平行与垂直》教学实践与反思（二）

居晓红

【教学内容】

人教版四年级上册第五单元。

【教学过程】

一、沟通经验，尝试表达

师：同学们，你们听说过“平行”和“垂直”吗？谁能说一说日常生活中的平行现象或垂直现象？

生：我们笔记本上的横线一条一条的就是平行。

生：学校操场上竖着的旗杆就是垂直。

师：你心目中的平行和垂直是什么样的？把你心目中的平行和垂直分别画在两张白纸上。

二、突破认知，探究本质

1.基于学生经验，展示原生认知。

师：现在让我们一起来看看同学们心目中的平行与垂直。

（请学生根据自己的理解将作品粘贴在黑板上的相应位置）

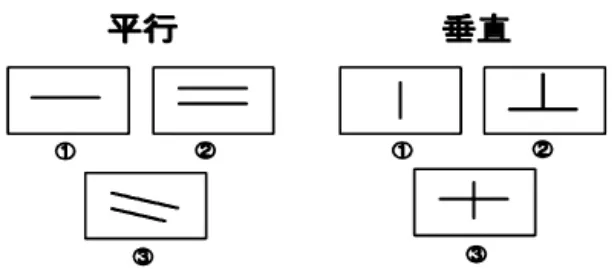
师：对黑板上的三组作品，同学们有什么疑问或想法吗？

生：为什么第一组作品都只有一条线，而其他作品都是两条线的？

生：我认为“平行组”里的③号作品不对，平行应该是平平的，它斜了。

生：“我认为“垂直组”的②号和③号作品都有问题，垂直应该是竖着并且直的线，而这两个作品中都出现了横的线。

师：同学们的问题和想法都很好，对平行和垂直也都有自己的理解。那到底谁说得是对的呢？我们一起来看看书上是怎么描述平行和垂直的。

2.对话教材文本，构建初步认知。

（1）自学教材，初步感知。

师：请同学们打开数学书第56、57 页，认真阅读并仔细观察书上的示例图，看看你能否对平行和垂直有新的认识。

（2）汇报交流，辨析修改。

师：自学完平行和垂直的定义后，你认为黑板上的三组作品需要修改吗？先同桌交流，统一你们的修改意见并说明理由。

生：我们组认为两个①号作品分别都要再添加一条横线，因为书上对平行和垂直的描述都是针对两条直线的。

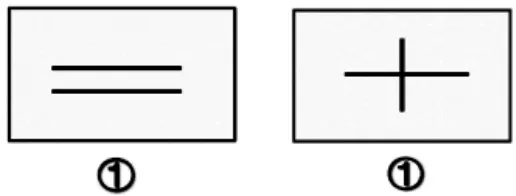
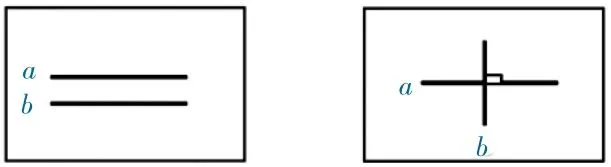
生：我们还有补充。可以把两条直线记作a 和b，垂直的情况还需要加上直角符号。

（3）对比本质，教学相交。

师：同学们的观察能力和自学能力真棒。请你对比平行和垂直两种情况，想一想它们最大的区别在哪里？

生：平行是不会交叉的，垂直会交叉。

生：书上说两条直线不相交叫互相平行，两条直线相交并且成直角叫互相垂直。

师：同学们说的两条直线交叉数学上叫做相交。

师：请同学们看这幅作品，判断两条直线平行吗？说说理由。

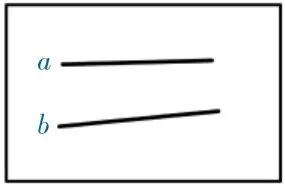
生：平行，因为两条直线没有相交。

生：不平行，这两条直线方向不一样，延长以后会在很远的地方相交。

师：谁听明白他的意思了？

生：直线可以向两端无限延长，所以他说这两条直线延长以后会在一边相交。

师：同学们，想象一下这两条直线向两端延长、继续延长、再延长后的样子，会在哪一边相交？请你们指一指。（课件同步动画演示）

师：两条直线相交以后的这个点我们叫它交点。

3.变化直线位置，概括垂直概念。

（1）看相交，体会垂直的本质。

课件出示：

师：这五组直线都相交吗？你能找到交点在哪里吗？

（根据学生回答课件演示直线延长的过程并标注交点位置）

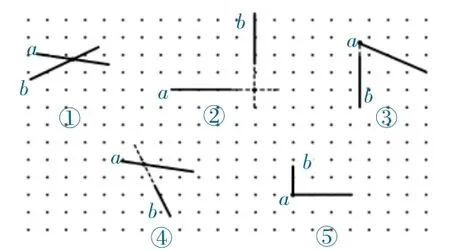
师：仔细观察这五组直线，你发现了什么相同点和不同点？

生：每一组直线都相交，都有一个交点。

生：两条相交的直线会形成角，每一组角的大小都不同。

生：第②组和第⑤组的角一样，都是直角，这两组线是互相垂直的。

师：判断两条直线是否相交成直角，光看可不行，可以怎么验证呢？

生：用三角板的直角去比一比。

师：（课件演示量一个直角的过程）老师已经验证了这个角是直角，可以了吗？

生：还不行，必须要检验四个角都是直角。

生：我们量一个角就行了，相邻的两个角是平角，知道了一个角是90°，就知道这个角边上的角就是180°减90°；同样的道理我们可以推导出另外的两个角也是90°。

师：真了不起，你用推理的方法发现两条直线相交时，形成的四个角中，如果有一个角是直角，那么其余的角也都是直角。

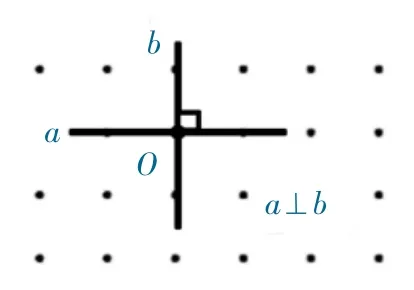
小结：其实两条直线相交的情况有无数种，其中相交成直角是非常特殊的一种情况，就如同课始自学的，我们把两条直线相交成直角的位置关系叫做互相垂直，记作a⊥b，读作a 垂直于b。我们可以说a 是b 的垂线，或者b 是a 的垂线。它们的交点叫垂足，用字母O 来表示。

（2）画垂直，感悟垂直的本质。

师：请同学们试着在点子图上画一组互相垂直的直线。

作品展示：

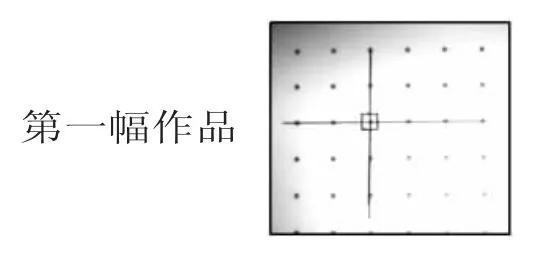
生：第一幅作品挺好的，但是我认为只要标一个直角符号就行了，因为四个角一样大，只要说明一个角是90°，就能知道其他三个角也是90°。

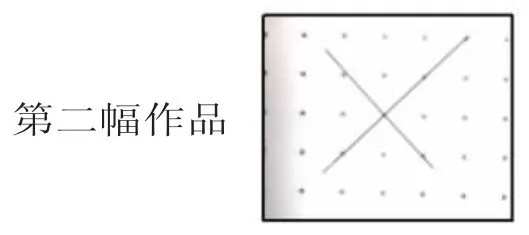
生：我认为第二幅作品不对，这两条直线斜了。

生：直线斜了没有关系，只要直线相交形成直角就行，但是这个作品没有标直角符号，我们需要用三角尺量一下，然后标上直角符号。

生：这个作品好像也有问题，只有两个直角。

生：只要把竖着的直线延长就好了，也是有四个直角的。

师：同学们的点评都非常好，已经从本质上认识了两条直线互相垂直的关系。

4.探究平行现象，感知平行本质。

师：我们已经知道了什么是相交，也知道两条直线相交有一种特殊情况叫互相垂直，那么在同一个平面内，两条直线的位置关系，除了相交，还有别的情况吗？

生：还有不相交。

师：是的，老师把之前的作品进行了修改，请判断现在直线a和直线b 是否相交？说明理由。

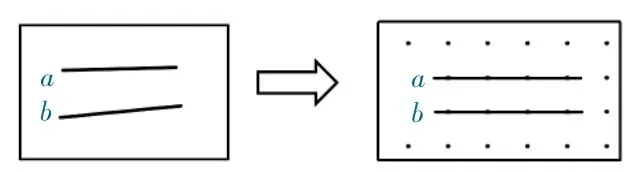
生：我认为这两条直线不会相交，因为它们的方向一样。

师：什么叫方向一样？

生：就是两条直线延长都是平平的往左右方向，一直不会碰到。

生：这两条直线之间的间隔都是两个点的距离，所以永远不会相交。

师：如果把这组直线这样旋转一下呢？还是不相交吗？（课件演示一组直线同时旋转的过程）

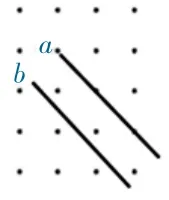
生：也不会相交，因为旋转后两条直线方向是一起变化的，还是保持了方向一致。

生：我认为，两条直线可以斜着、可以平着，但是，中间的长度（距离）如果没有变化，就不会相交，这样就叫互相平行。

师：正如我们在数学书上自学到的，在同一平面内，不相交的两条直线叫平行线，也可以说这两条直线互相平行。用字母表示a//b，我们可以说a 是b 的平行线或者b 是a 的平行线。

5.借助几何直观，突破“同一平面”。

师：请大家思考一下，是不是只要两条直线永不相交，那么这样的两条直线就互相平行呢？

生：是。

出示长方体：

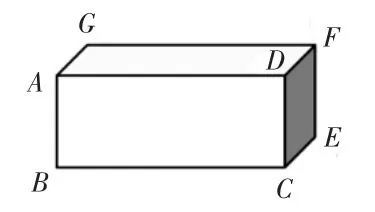
师：你能在这个长方体上找出互相平行的线段吗？

生：AB∥DC、DC∥FE。

生：AG∥DF、DF∥CE、BC∥AD、AD∥GF。

师：观察一下BC 和DF 会相交吗？（课件同步演示这两条线段所在直线延长的过程）

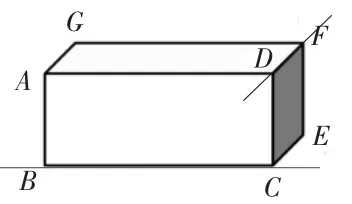
生：不会相交。

师：那它们互相平行吗？

生：也不是平行的。

师：既然不相交，这两条直线怎么也不平行呢？小组交流讨论。

生：它们的方向不一样，所以不相交。

生：我还有补充，因为这两条直线不在同一面上。

生：我们组的结论是两条直线互相平行有一个前提，必须是在同一平面内的两条直线，比如这两条直线，一条在前面，一条在右面，永远不会相交，但是也不是互相平行的。

师：看来，只有在同一个平面内的两条直线不相交才互相平行，你们真棒！

三、巩固练习，统一认知

1.解决问题，内化认知。

师：下图中哪些直线互相平行？哪些直线互相垂直？用字母表达的方式分别记录在《学习单》上。

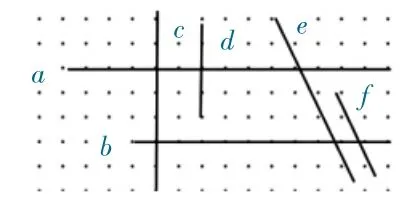
2.空间想象，以问促学。

师：d 和b 是什么位置关系？

生：互相垂直，把d 延长就行。

师：c 和f 是什么位置关系？

生：它们没有关系，既不是相交也不是平行。

师：想象，如果c 和f 都无限延长……

生：会在很远的地方相交！

师：同学们真厉害，虽然图上只画了一段，但是直线是可以无限延长的，所以c 和f 会在上面某处相交。

3.梳理关系，形成体系。

师：根据这节课的学习，如果把同一平面内的直线位置关系分类，你会怎么分呢？

生：相交和不相交。

师：同一平面内，不相交的两条直线互相平行。（板书：互相平行）

生：我还有补充，相交里面还有一类垂直。（板书：垂直）

四、回归生活，全课小结

师：生活中像这样平行和垂直的现象很多，让我们带着数学的眼光来观察周围的世界。（欣赏生活中的平行与垂直，略）

师：最后回顾一下，这节课我们是怎么认识平行和垂直的？

（课件出示：自学教材→认识相交→感知垂直→认识平行→同一平面）

【教学反思】

一堂好的课需要执教者明确学生的知识起点，真正站到学生学的角度去思考和设计，以学生原有知识经验为基础，然后有针对性地寻求变化或突破的办法。本节课笔者力求紧扣核心目标，充分尊重学生已有的生活经验和认知路径，以任务驱动让学生发展数学抽象能力和空间观念。

一、尊重学生的学习起点

在学习本节课前学生已经认识了直线、线段和射线等几何图形，同时也对生活中的平行现象和垂直现象有自己的认识和经验。大部分学生能直观感知生活中的平行和垂直，但不会用数学的语言来表示。因此笔者在课始就设计了让学生说一说自己对平行和垂直的理解，画一画自己心目中的平行和垂直。对比以往教学时，需要让学生在分类中体会“相交”。学生在进行分类时，往往根据不同标准会产生不同的分类情况，而教师最后还是要引导学生按照“是不是相交”的关系来分类，这样的“分类”耗费大量课堂时间。笔者在设计本课时开门见山提出“平行”和“垂直”两类，让学生的知识起点充分暴露，同时教师能快速进入主题，了解学生原始认知状态。

二、呈现学生的学习过程

本节课笔者基于学生的生活经验，借助“体验——自学——辨析——归纳——修正”的学习历程，让学生在活动中自主经历数学抽象。第一次画自己认为的平行和垂直，这是基于原有经验的抽象活动；第二次学生在自学教材后，根据自己的理解修改同学作品并讨论辨析，这是理解表达的抽象活动；紧接着以“相交”为主线，学生通过自主探索、合作交流，经历“相交”“垂直”“平行”三个概念的形成过程，这是内化本质的抽象活动。此时学生头脑中已经有了丰富的几何表象，教师只需要顺势利导，呈现概念即可完成教学目标。

三、相信学生的自学能力

平行和垂直是两条直线位置关系的特殊情况，而学生对平行和垂直的经验来自于生活中的这种特殊现象，笔者在教学设计中直接让学生画平行和垂直是符合学生认知的。同时放手让学生自学，通过看书交流、修改讨论、辨析内化的过程，学生不断通过自主学习修正自己的认知偏差。在这样的课堂上，教师充分相信学生的自学能力，学生把握了学习的主动权，这样的学习过程是有体验、有经历、有思考的，这是达成学生自主学习的有效方式。

以上仅是自己粗浅的思考和实践，不当之处，恳请各位方家批评指正！