一种优化共同邻居影响的动态距离社区发现算法

万甲鑫

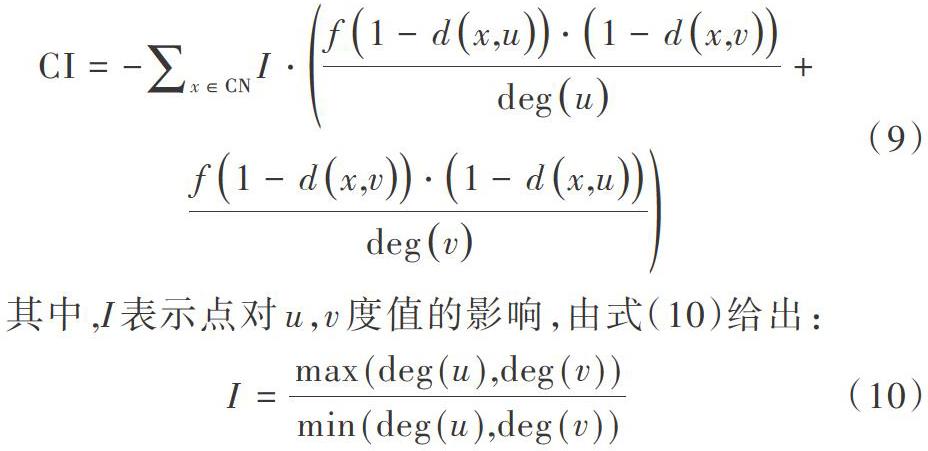
摘 要：在众多社区发现算法中，Attractor算法是一种快速的社区发现算法，具有社区检测准确率高的优点。为解决Attractor算法在距离更新过程中节点对度值相差太大，影响小度节点所属社区判断问题，提出一种优化共同邻居影响的Attractor社区发现算法。该算法在Attractor算法提出的动态距离节点交互模型基础上，考虑节点对两者度值差异，通过在节点对与共同邻居交互模式中增加一个大度节点不利系数，以增加小度节点对邻居的吸引作用。采用LFR基准网络，在不同结构网络上验证改进算法的有效性。实验结果表明，改进算法与Attractor算法相比社区发现准确度更高。

关键词：社区发现;复杂网络;动态演化;动态距离

DOI：10. 11907/rjdk. 201350

中图分类号：TP312文献标识码：A 文章编号：1672-7800（2020）010-0142-04

Abstract： Among many community discovery algorithms， the attractor algorithm is a fast community discovery algorithm， and has the advantages of high community detection accuracy. In order to solve the problem that the difference of degree value between nodes in the process of distance update affects the community judgment of small degree nodes， a community discovery algorithm of attractor which optimizes the influence of common neighbors is proposed. Based on the dynamic distance node interaction model proposed by the attractor algorithm， this algorithm takes into account the difference of the degree values between the two nodes. By adding a negative coefficient of large nodes in the interaction mode between the node pair and the common neighbor， the attraction of the small node to the neighbor is increased， and the LFR benchmark network is used to verify the effectiveness of the improved algorithm on different networks.

Key Words： community detection; complex network; dynamic evolution; distance dynamics

0 引言

近年來，复杂网络理论与研究方法越来越多地应用于真实世界的复杂系统中，如蛋白质网络研究、计算机网络路由分析、交通网络路径规划以及新闻传播学等领域[1-3]。许多复杂系统可以用图表示，通过定义规则，将一个组件或实体抽象为一个节点，而组件或实体之间的连接描述为节点之间的连边[4]。

为更进一步探索复杂系统内部潜在的结构特征，复杂网络的社区发现方向成为研究热点[5-8]。受到网络动力学启发，邵俊明等[9]提出基于节点间的距离动力学划分社区Attractor算法，通过模拟节点间距离的动态演化，最终发现网络的潜在社区结构。Attractor算法可直接根据网络拓扑结构得到社区划分结果，划分结果准确，并且可以发现不同规模大小社区，且时间复杂度较低，适用于大规模网络;文献[10]将动态距离模型扩展到两部分图中，验证了动态距离在多属性图中的有效性;文献[11]研究先验知识对Attractor算法的影响，提出的半监督Attracotor算法在有先验知识情况下可获得非常高的准确度;文献[12]利用网络三角结构压缩原始网络，并通过计算社区相似度将Attracotor用于重叠社区检测，获得较好结果。

以上方法都对Attracotor算法的高准确度和可扩展性作了深入研究，但是对Attractor算法的交互模式研究还比较少。本文在研究度值相差较大的节点对距离变化影响情况后，通过引入大度节点不利系数[13]，改进共同邻居交互模式对节点距离的影响。在带有真实社区标注网络上进行实验，验证改进算法可提升社区划分准确度。

1 基于动态距离的Attractor算法

Attractor算法中的动态距离交互模型将网络看作一个节点间距离不断变化的动态系统。系统初始时刻，每对节点都有一个初始距离，随着系统逐渐演化，节点会和周围的邻居节点产生交互，而这些交互行为会造成节点间距离改变。节点邻居分为3种类型，节点与不同类型的邻居交互会对节点间距离产生不同影响。3种类型邻居分别为两个节点自身、节点对的共同邻居以及节点对各自的独有邻居。节点在3种邻居影响下距离会逐渐变化，一些节点对之间的距离逐渐减小，最终减小到最小值0，则该对节点属于同一个社区。相反，另一些节点距离会慢慢增加，最终增加到最大值1，则该对节点属于不同社区。

1.1 相关定义

1.2 动态距离交互模型

节点[u]和节点[v]会与周围3种不同类型的邻居产生交互，这些交互会对距离[d（u，v）]产生影响，3种交互模式如下：

（1）直接连接影响。节点[u]和节点[v]直接连接的交互模式会吸引两者互相靠近，造成距离[d（u，v）]减小，使用函数DI表示如下：

（2）共同邻居影响。节点[u]和节点[v]与共同邻居[CN=Γu∩Γ（v）]的交互也会吸引两者互相靠近，造成距离[d（u，v）]减小，使用函数CI表示如下：

（3）独有邻居影响。节点[u]和节点[v]与各自独有邻居[ENu]、[ENv]的交互也会对距离[d（u，v）]产生影响。但由于节点的独有邻居和另一端节点没有连接，无法直接判断节点[u]的独有邻居会造成距离[d（u，v）]增加还是减小。Attractor算法使用一个凝聚参数[λ]决定独有邻居对[d（u，v）]的影响，如式（6）所示。

其中，[ρ（x，y）]表示节点[u]的独有邻居[x]对[d（u，v）]是正影响还是负影响。[d（x，v）]表示独有邻居[x]和节点[v]之间的距离，[1-d（x，v）]表示独有邻居[x]和节点[v]之间的相似性。当相似性大于阈值[λ]时，[ρ（x，y）]为正值，则独有邻居[x]和节点[u]交互会引起[d（u，v）]减小;当相似性小于阈值[λ]时，[ρ（x，y）]为负值，会引起[d（u，v）]增加。独有邻居影响可用函数EI表示。

通过以上3种交互模式作用，可得到节点间在[t+1]时刻的距离更新值[d（u，v;t+1）]，如式（8）所示。

2 改进Attractor算法

2.1 改进方法

Attractor算法在计算初始距离时，大度节点与其周围邻居距离都非常接近于1。如果大度节点的邻居度值较小，且两者共同邻居数很少，则根据式（8）计算的距离更新量一直都在增加，小度节点在距离演化过程中会逐渐远离周围大度邻居，最终与所有的大度邻居距离都为1，单独位于一个社区。为降低大度节点对周围邻居距离更新的影响，考虑给共同邻居交互模式CI增加一个大度节点不利系数，以此消弱小度节点和大度节点的度值差异。改进后的CI如式（9）所示。

如果两者度值比较接近，则改进后的CI对原有CI影响不大;如果两者度值相差较大，则改进后的CI可有效消除大度节点对距离更新的影响。

2.2 算法流程

（1）初始状态下，使用Jaccard距离计算[t=0]时网络中所有节点对间距离。

（2）根据式（4）、式（7）、式（9）分别计算DI、改进后的CI、EI，然后根据式（8）得到每个节点对下一时刻的距离更新量[d（u，v;t+1）]。

（3）判断当前距离更新量[d（u，v;t+1）]是否大于0或小于1。如果小于0，则认为距离达到最小值0，同时不再更新该节点对距离;如果大于1，则认为距离达到最大值1并不再更新该节点对距离。

（4）重复步骤（2）、步骤（3），直到所有距离都收敛到0或1。

（5）删除距离等于1的边，最终得到网络中的社区结构。

3 实验分析

对比改进算法和Attractor算法在不同结构人工合成网络上的结果。在同一组参数下，人工合成网络生成20个网络，然后取这20个网络评价指标的平均值作为该组参数最终实验结果。

3.1 评价指标

标准化互信息[14]（Normalized Mutual Information，NMI）用于评价实际社区和算法划分出来的社区相似程度。NMI取值范围在0和1之间，如式（12）所示。

其中，[X]表示算法划分的社区结构，[Y]表示真实社区结构，[I（X，Y）]表示[X，Y]的互信息，[H（X），H（Y）]分别表示[X，Y]的信息熵。NMI值越高，表示[X，Y]越相似。

模块度[15]（Modularity）是另一种衡量社区划分质量评价指标。计算模块度不需要知道真实社区结构，而是与网络相应的零模型作比较，度量算法划分结果质量。模块度取值范围在0和1之间，表示如下：

其中[，m]是网络边数，[A]是网络邻接矩阵，[Aij]表示边[e=（i，j）]的权值，无权网络中为1，[ki]表示节点[i]的度值，[ci]表示节点[i]的社区，[δ（?）]是克罗内克函数，如果节点[i]、[j]位于同一个社区，[δ（ci，cj）]等于1，否则等于0。

3.2 实验结果

为评估改进算法与原算法在社区检测准确度上的差异，采用LFR[16]人工合成网络作为评测网络，以NMI和模块度值作为准确度评价指标。

首先控制网络平均度从5变化到20，对比改进算法和Attractor的实验结果。网络其它参数为：网络节点数[N=2 000]，混合参数[μ=0.5]，最大度值[kmax=50]，度分布参数[γ]=2，社区大小分布参数[β=1]，最小社区大小[Cmin=10]，最大社区大小[Cmax=50]。

实验结果如图1所示，可以看出改進算法在平均度较大的网络上准确度明显提升。当平均度较小时（[k]=5），改进算法和Attractor的NMI值与模块度值几乎一样。但随着[k]增加到10和15时，改进算法准确度提升最大。当[k]增加到20和25时，准确度提升不是很明显。

生成两种不同社区大小的LFR基准网络，控制网络最小社区大小和最大网络社区大小分别为[Cmin=10]、[Cmax=50]以及[Cmin=20]、[Cmax=100]，并且控制混合参数[μ]从0.1变化到0.8。网络其它参数分别固定为：网络节点数[N=1 000]，平均度[k=20]，最大度值[kmax=50]，度分布参数[γ]=2，社区大小分布参数[β=1]。混合参数[μ]可用来控制网络的社区结构复杂度，[μ]越大表示社区结构越复杂，社区划分也越困难。

图2显示两种算法在社区大小位于10～50之间网络上的比较结果。由图2可知，当混合参数小于0.2时，两种算法都能准确检测出社区，此时NMI值为1。当混合参数在0.3～0.6之间时，改进算法带来的提升逐渐显现出来。当混合参数大于0.6的时候，由于网络社区结构变得复杂，即多数节点度值相差不多，改进算法和Attractor算法几乎一样。

如图3所示，当社区大小位于20～100之间时，改进算法获得明显提升。当混合参数μ小于0.4时，改进算法在NMI值上明显高于Attractor算法。随着混合参数的逐渐增大，改进算法提升效果逐渐减小，不过仍好于Attractor算法，能更好地检测出网络中的社区结构。

4 结语

本文提出一种改进的Attractor社区发现算法。在Attractor算法动态距离交互模型中，针对大度节点影响周围节点距离更新问题，引入大度节点不利系数，改进共同邻居交互影响公式，提高了社区发现准确度。实验结果表明，改进算法可在多个网络上获得更高的NMI值和模块度值，准确度更高，且在社区规模较大的网络中效果更明显。后续将研究节点对度值差异对另外两种交互模式的影响，以期获得更高的社区发现准确度。

参考文献：

[1] FORTUNATO S. Community detection in graphs[J].  Physics reports， 2010， 486（3-5）： 75-174.

[2] FORTUNATO S， HRIC D. Community detection in networks： a user guide[J].  Physics reports， 2016， 659（9）： 1-44.

[3] 骆志刚， 丁凡， 蒋晓舟，等.  复杂网络社团发现算法研究新进展[J].  国防科技大学学报， 2011， 33（1）：47-52.

[4] 汪小帆， 李翔， 陈关荣.  网络科学导论[M].  北京：高等教育出版社， 2012.

[5] HRIC D， DARST R K， FORTUNATO S. Community detection in networks： structural communities versus ground truth[J].  Physical Review E， 2014， 90（6）： 62-80.

[6] 李磊，倪林. 基于模块度优化的标签传播社区发现算法[J]. 计算机系统应用，2016，25（9）：212-215.

[7] 刘苗苗，郭景峰，马晓阳，等. 基于共邻节点相似度的加权网络社区发现方法[J]. 四川大学学报（自然科学版），2018，55（1）：89-98.

[8] 王莉，程学旗. 在线社会网络的动态社区发现及演化[J]. 计算机学报，2015，38（2）：219-237.

[9] SHAO J， HAN Z， YANG Q， et al. Community detection based on distance dynamics[C]. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM， 2015： 1075-1084.

[10] SUN H， CHNG E， YONG X， et al. A fast community detection method in bipartite networks by distance dynamics[J].  Physica A： Statistical Mechanics and its Applications，2018， 496（15）：108-120.

[11] FAN L， XU S， LIU D， et al. Semi-supervised community detection based on distance dynamics[J].  IEEE Access， 2018， 6（9）： 37261-37271.

[12] XIANG B， GUO K， LIU Z， et al. An overlapping community detection algorithm based on triangle coarsening and dynamic distance[C]. CCF Conference on Computer Supported Cooperative Work and Social Computing，Springer， Singapore， 2018： 285-300.

[13] 吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报，2010，39（5）： 651-661.

[14] STREHL A， GHOSH J. Cluster ensembles——a knowledge reuse framework for combining multiple partitions[J].  Journal of machine learning research， 2002， 3（12）： 583-617.

[15] NEWMAN M E J. Modularity and community structure in networks[J].  Proceedings of the national academy of sciences， 2006， 103（23）： 8577-8582.

[16] LANCICHINETTI A， FORTUNATO S， RADICCHI F. Benchmark graphs for testing community detection algorithms[J].  Physical review E， 2008， 78（4）： 46-110.

（責任编辑：杜能钢）