基于BP-SVR组合模型的空气质量指数预测

甘露情 刘媛华

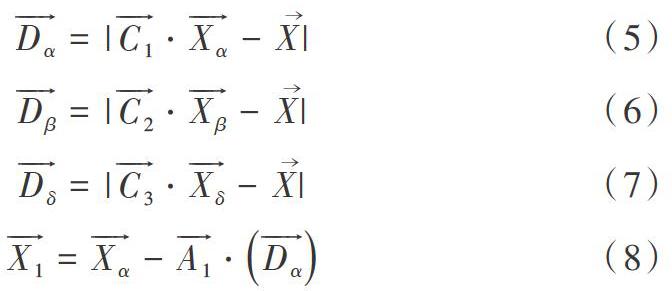
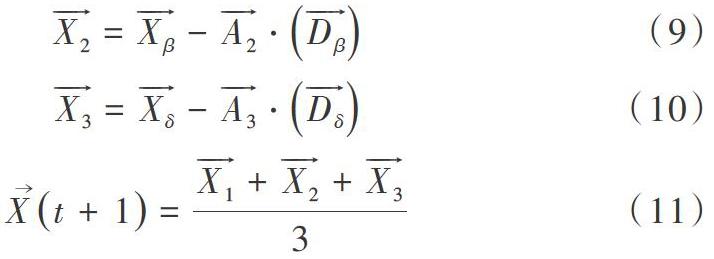
摘 要：建立有效的空气质量指数预测模型，可以为个人出行及相关部门治理大气污染提供指导。选取北京市的历史空气数据以及气象数据作为研究对象，建立基于BP（Back Propagation）神经网络和SVR（Support Vector Regression）支持向量机回归的BP-SVR组合预测模型。首先利用灰狼优化算法分别对BP模型和SVR模型参数进行寻优;然后运用该组合模型对空气质量指数进行预测。实验结果表明，BP-SVR模型的平均绝对百分误差、均方根误差、平均绝对误差均小于单一预测模型，分别为0.217 5、37.032 0、25.157 5。BP-SVR组合模型具有更高的预测精度，泛化能力更强，可以对空气质量指数进行有效预测。

关键词：空气质量指数预测;灰狼算法;BP模型;SVR模型;BP-SVR模型

DOI：10. 11907/rjdk. 201217

中图分类号：TP301文献标识码：A 文章编号：1672-7800（2020）010-0080-04

Abstract： Establishing an effective air quality index prediction model can provide guidance for individual travel and related departments to control air pollution. The historical air data and meteorological data of Beijing were selected as research objects， and a BP-SVR combined prediction model based on BP （Back Propagation） neural network and SVR （Support Vector Regression） support vector machine regression was established. First， the gray wolf optimization algorithm was used to optimize the parameters of the BP model and the SVR model， and then the combined model was used to predict the air quality index. Experimental results show that the average absolute percentage error， root mean square error， and average absolute error of the BP-SVR model are smaller than that of a single prediction model， which are 0.2175， 37.032 0， and 25.157 5， respectively. The BP-SVR combination model has higher prediction accuracy and stronger generalization ability， and can effectively predict the air quality index.

Key Words： air quality index prediction; gray wolf algorithm; BP model; SVR model; BP-SVR model

0 引言

我国工业化进程不断加快，能源消耗量持续增加，产生大量的污染颗粒，导致我国空气污染日趋严峻[1-2]。近些年，我国众多城市出现大规模雾霾天气的频率越来越高，特别是2015年北京发生史上最严重雾霾，PM2.5浓度峰值接近1 000μg/m3。空气污染不但会对人体健康造成伤害，还会造成交通停滞等问题，对社会经济造成重大损失[3]。目前亟需建立模型对空气质量指数进行有效预测，减少大气污染对人体的危害，还可为相关部门治理大气污染提供数据支持。

国内外早期主要从数值模型和统计模型角度预测空气质量指数，数值模型需要对污染物有充分认识，数据采集难度较大。统计模型计算简单，然而空气质量数据具有非线性特点，用线性模型进行预测难以取得较好结果。由于神经网络具有较强的非线性拟合能力，越来越多的学者采用神经网络对空气质量指数进行预测。如Mishra等[4]分别建立人工神经网络和多元线性回归模型对印度德里的PM2.5值进行预测，实验结果证明神经网络模型的预测精度更高;吕霁洲[5]首先提出简化AQI计算模型并进行验证，又提出采用BP神经网络模型对AQI进行预测，对北京某地区空气质量进行预测，结果表明当数据量足够时可以达到很高的预测精度。单一预测模型初始参数设置会对预测结果产生较大影响，为了进一步提高预测精度，越来越多学者提出将单一模型与其它方法相结合的混合模型。Feng等[6]提出将小波分析和轨迹分析与BP神经网络相结合的模型，并应用于PM2.5浓度预测;张楠等[7]采用改进灰狼算法优化支持向量机回归模型，构建空气质量指数预测模型，对太原市空气质量进行预测，结果表明该模型具有更高的预测精度;吴慧静等[8]利用遗传算法优化神经网络构建空气质量指数预测模型，对许昌市空气质量进行预测验证，并与单一神经网络对比，表明该模型具有更高的预测精度。目前，空氣质量指数预测鲜少考虑气象因素影响，且很少将两种预测模型进行组合预测。本文在分析空气质量影响因素过程中考虑气象条件，利用灰狼优化算法分别对神经网络和支持向量机参数进行优化，再对空气质量分别加以预测，将两者预测结果作非线性处理，得到空气质量指数最终预测结果。

1 基于GWO算法的BP神经网络与SVR优化

1.1 灰狼优化算法

灰狼优化算法（GWO）是由澳大利亚学者Mirjalili等[9]提出的一种群智能优化算法。灰狼处于食物链的顶层，内部拥有非常严格的社会等级制度[10]。GWO算法将狼群根据适应能力大小从高到低分成a、b、d、w 4个等级[11]。数学模型如下：

（1）包围猎物。灰狼搜索猎物时需接近并包围猎物，该行为数学模型为：

式中，t是算法當前迭代次数，[A]和[C]是协同系数向量，[Xp]表示猎物当前位置向量，[Xt] 表示灰狼在第t次迭代时的位置向量，在整个迭代过程中，[a]的值从2线性降到0;[r1]和[r2]是[0，1]中的随机向量。

（2）狩猎。搜索猎物过程中，假设a、b、d在识别潜在猎物位置具有较强能力，因此根据种群中最好的3只灰狼的位置信息更新其余搜索代理位置信息，数学表达式如下：

（3）攻击猎物。灰狼捕获到猎物，即GWO算法找到最优解。[A]的值会随着[a]的线性递减而变化，当|[A]|>1，灰狼远离猎物;|[A]|<1，灰狼攻击猎物，找到最优解。

1.2 GWO优化BP神经网络参数寻优

BP神经网络是一种多层前馈神经网络，该网络最主要的特点是信号前向传播，误差反向传播[12-13]。本文采用的神经网络结构层数为3层，分别为输入层、隐含层、输出层。网络初始权值和阈值的随机性对BP神经网络模型的预测性能影响较大，使其容易陷入局部最优解，收敛速度慢[14-16]。因此，本文利用GWO算法优化BP神经网络的初始权值和阈值，提高模型预测精度。

具体步骤如下：①确定神经网络结构，随机初始化权值和阈值;②初始化灰狼算法参数，初始化不同等级灰狼的位置向量;③计算灰狼适应度值，若优于原来的适应度值，则将该狼的适应度值作为最佳适应度值，否则保持原有结果继续迭代;④达到最大迭代次数，输出最优权值和阈值，否则继续步骤③进行迭代寻优;⑤将最优权值和阈值输入BP神经网络，并进行下一步预测。

1.3 基于GWO优化算法的SVR参数寻优

支持向量机最早由Vapnik提出，具有较好泛化性能，需优化参数少、计算简单[17-18]。但SVR模型预测精度受惩罚参数c和核函数参数g影响较大，目前对参数选取并没有公认统一的最佳方法[19-20]。本文利用灰狼优化算法全局搜索能力强的优点，在更大范围内对SVR的c和g参数进行寻优。具体步骤如下：①初始化支持向量机参数范围;②初始化灰狼算法参数，确定灰狼数量，初始化不同等级灰狼位置向量;③以均方根误差作为优化的目标函数值，计算灰狼适应度值;④更新灰狼位置向量，计算更新后的灰狼适应度，若适应度值优于原来最佳适应度值，则将该灰狼适应度值作为最佳适应度值，否则继续迭代;⑤若达到最大迭代次数，输出最优参数c和g，否则返回步骤④继续迭代;⑥将最优参数c和g输入SVR模型中进行训练和预测。

2 BP-SVR组合模型

由于空气质量数据具有非线性和时序性特征，用单一模型对其进行预测，准确率不高。BP神经网络模型能够较好模拟非线性数据，适合中长期预测，泛化能力强。SVR模型是一种短期的基于时间序列的回归模型。将两者进行组合预测，能提高模型预测精度。

组合模型结构如图1所示，将经过预处理的数据集分成训练集（Traindata）和测试集（Testdata），先将训练数据集分别输入GWO-BP和GWO-SVR算法中进行训练，得到最优BP模型（M1）和SVR模型（M2），再将测试集分别输入BP和SVR模型中，得到两组预测结果R1和R2。大多数组合模型将预测结果进行直接相加处理，忽略简单线性处理弊端。本文利用人工神经网络对组合模型的权重系数进行优化，对两组预测结果赋予最佳权重系数，得到最终预测值。首先将真实数据（P）和两组预测数据组成新的数据集（Newdata），将数据集分成训练集（Newdata_Train）和测试集（Newdata_Test）;再利用BP神经网络算法对新的训练集进行训练，得到第2个BP模型（M3）;最后将测试集（newdata_test）输入模型（M3）进行预测，得到最终预测结果。

3 实验与结果分析

3.1 数据预处理

本文数据来源于中国环境监测总站和中国气象局，选取北京市2013年12月2日-2017年2月28日的AQI数据和6种污染物数据，以及同时期气象数据，共1 184天数据。污染物数据包括NO2、CO、PM2.5、PM10、SO2、O3，气象数据包括风速、气压、气温。实验中将前一天的空气污染物数据以及当天气象数据作为输入因素，当日的AQI数据作为输出量。输入模型前先对数据作归一化处理，消除因数量级不同对预测精度造成的影响。

3.2 模型训练

（1）GWO-BP算法中，灰狼数量为30，迭代次数为100。经过训练，当BP神经网络隐含层数量为10个时，误差最小，因此BP神经网络结构为9-10-1。GWO-SVR算法中的灰狼种群数量为30，迭代次数为100。

（2）将经过预处理后数据集中的1 000组数据作为训练集数据（Traindata），剩余的186组数据作为测试集数据（Testdata）。利用训练集数据训练GWO-BP和GWO-SVR算法，得到模型M1和M2。利用模型M1和M2对测试集数据进行预测，将得到的两组预测结果R1和R2和真实数据组成新的数据集（Newdata）。从新的数据集中选取100组数据作为新的训练集（Newdata_Train），剩余的86组数据作为新的测试数据集（Newdata_Test）。利用Newdata_Train训练新的BP神经网络，当隐含层数量为5时，预测精度最高，得到模型M3。将新的测试集输入模型M3中得到最终预测值。

3.3 实验结果分析

将本文提出的BP-SVR组合模型、BP模型及SVR模型进行对比，验证本文空气质量指数预测模型有效性。将相同数据集输入BP和SVR模型中，实验结果如图2所示。

由图2可以看出，本文提出的BP-SVR模型比单一BP模型和SVR模型数据预测拟合能力更强。BP-SVR模型预测趋势更接近于真实值，但仍有部分点预测效果较差。

模型误差曲线对比如图3所示。

由图3可以看出，BP-SVR组合模型比单一BP预测模型和SVR预测模型具有更小的预测误差。为了对不同模型预测结果作进一步分析，引入3个量化评价指标，即平均绝对百分误差（MAPE）、均方根误差（RMSE）、平均绝对误差（MAE），结果如表1所示。

由表1可以看出，BP-SVR组合预测模型的均方根误差、平均绝对误差、平均绝对误差百分比均明显小于单一BP模型和SVR模型，模型预测精度提高，数据拟合能力更强。

4 结语

空气质量指数预测是一个复杂问题，不仅受污染颗粒影响，还受气象因素影响较大。对其进行有效预测，可为人们日常生产活动及空气污染治理提供指导。本文在考虑气象因素的基础上，针对单一预测模型精度不高的问题，提出BP-SVR组合预测模型，对空气质量指数进行预测。根据误差对比和指标评价结果可知，BP-SVR模型预测精度比单一预测模型更高，拟合能力更强。因此，该模型可有效应用于空气质量指数预测，但仍有部分点预测效果不佳。后续将对数据进行离群点检测，进一步提高模型预测精度。

参考文献：

[1] 王继志，杨元琴，周春红，等. 雾霾能见度天气分析与预测方法研究[C]. 中国气象学会会议论文集，2007：152-156.

[2] 齐甜方，蒋洪迅，石晓文. 面向多源数据沈阳市 PM2.5浓度预测研究及实证分析[J]. 系统工程，2018（5）：104-115.

[3] 王建州，杨文栋. 基于非线性修正策略的空气质量预警系统研究[J]. 系统工程理论与实践，2019，39（8）：2139-2151

[4] MISHRA D，GOYAL P，UPADHYAY A.Artificial intelligence based approach to forecast PM2.5 during haze episodes：A case study of Delhi，India[J]. Atmospheric Environment，2015，102：239-248.

[5] 吕霁洲. 基于AQI和BP神经网络的空气质量评价及预测[J]. 电子世界，2018，38（11）：23-24.

[6] FENG X，LI Q，ZHU Y J，et al. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation[J]. Atmospheric Environment，2015，107： 118-128.

[7] 张楠，王鹏，白艳萍，等. 基于MGWO-SVR的空气质量预测[J]. 数学的实践与认识，2018，49（8）：159-165.

[8] 吴慧静，赫晓慧. 基于GA-BP神经网络的空气质量指数预测研究[J]. 安徽师范大学学报，2019，63（4）：360-365.

[9] MIRJALILI S， MIRJALILI S M，LEWIS A.Grey wolf optimizer [J].  Advance In Engineering Software，2014（5）：46-61.

[10] 杨书杰，叶霞，李俊山. 基于灰狼算法的BP神经网络图像回复算法[J]. 微电子学与计算机，2018，47（3）：19-22，27.

[11] 徐达宇，丁帅. 改进GWO优化SVM的云计算资源负载短期预测研究[J].  计算机工程与应用，2015，52（12）： 1-7.

[12] 李雪，顾沈明，年浩. 改進粒子群算法优化BP神经网络的粮食产量预测[J]. 闽南师范大学学报（自然科学版），2014（1）：56-61.

[13] 祝翠玲，蒋志方，王强. 基于B-P神经网络的环境空气质量预测模型[J]. 计算机工程与应用，2007，44（22）：223-227.

[14] 马晓敏，王新. 基于遗传算法的BP神经网络改进[J]. 云南大学学报（自然科学版），2013，35（A2）：34-38.

[15] 付晓明，王福林，尚家杰. 基于多子代遗传算法优化BP神经网络[J]. 计算机仿真，2016，33（3）：258-263.

[16] 马秋芳. 改进PSO优化的BP神经网络短时交通流预测[J]. 计算机仿真，2019，35（4）：94-98，323.

[17] 尹琪，胡红萍，白艳萍，等. 基于GA-SVM的太原市空气质量指数预测[J]. 数学的实践与认识，2017，48（12）：113-120.

[18] 倪志伟，朱旭辉，程美英. 基于人工鱼群和分形维数融合 SVM 的空气质量预测方法[J]. 模式识别与人工智能，2016，28（12）：1122-1131.

[19] 王小川，史峰，郁磊，等. MATLAB神经网络43个案例分析[M]. 北京：北京航空航天大学出版社，2013.

[20] 高帅，胡红萍，李洋，等. 基于MFO-SVM的空气质量指数预测[J]. 中北大学学报，2018，40（4）：373-379.

（责任编辑：孙 娟）