覆盖双向S-粗集模型的构造及其拓扑性质研究

田卫章

(商丘职业技术学院，河南 商丘 476100)

引言

现今，研究人员都已经充分认知到，在Z.Pawlak所提出的粗糙集模型内，论域上的等价关系发挥着非常关键性的作用.首先，在等价关系基础上形成划分；其次，再进行论域上的上近似算子以及下近似算子的构建，即进一步精确概念，用于对不精确对象进行刻划；最后，更加深入地探究相关的知识获取以及知识约简方面的问题[1-4].

然而，对于诸多实际应用而言，构建对象之间的等价关系存在极大的难度，甚至在对象之间就本质层面而言并非存在等价关系，某些情况下论域也不具备静态性特征.出于使粗糙集理论与应用对象得到有效扩大的目的，基于相应的研究问题，研究者对Z.Pawlak所提出的粗糙集模型开展了多元化、多样化的推广.在此过程中有诸多理论模型先后被提出，包括模糊粗糙集模型、程度粗糙集模型、粗糙集模糊模型、变精度粗糙集模型、以动态集合为基础的S-粗糙集模型[5-6]与以覆盖理论为基础的S-粗糙集模型[7]等.本文在文献[7]的基础上，对覆盖双向S-粗糙集模型以及此类模型的部分性质展开了更为深入的探究.

1 预备知识

1982年，波兰数学家Z.Pawlak提出了粗糙集理论.其作为一类数学工具主要用于处理不确定知识.当前，粗糙集理论被广泛用在机器学习、数据挖掘以及模式识别等领域.然而，在经典粗糙集模型中，虽然等价关系发挥着非常关键的作用，但等价关系的规定太过严格，由于等价关系只能够解决部分完备信息系统，如此在一定程度上对粗糙集理论的应用产生了限制.在现实应用中，诸多研究人员对经典粗糙集模型实施了推广处理，即推广为包括相似关系等在内的其它关系，由此来促进此模型的发展.

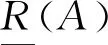
其中[x]R={y∈U;(x,y)∈R}为x关于R的等价类.下近似与上近似也可用下面的等式表达：

定义2(以覆盖理论为基础的S-粗糙集模型)假定X*为论域U上的双向S-集合，X*⊂U；f∈F为论域U上定义的元素迁移，而且

X*=X′∪{u|u∈U,u∉X,f(u)∈X} 其中X′是X的亏集[5].

如果记(R,F)°(X*),(R,F)°(X*)分别是X*⊂U的下近似，上近似，则有

(R,F)°(X*)=∪[x]R={x|x∈[f(x)]R∪[x]R⊆X*}

(R,F)°(X*)=∪[x]R={x|x∈[f(x)]R∩X*≠φΛ[x]R∩X*≠φ}

定义3[5]集合对((R,F)°(X*),(R,F)°(X*))叫做X*的双向S-粗集. 为了书写方便，本文用U±表示双向S-粗集.

定义4设U±是双向S-粗集，P(U±)是U±的双向S-粗子集族，C⊆P(U±)，如果φ∉C且∪C⊇U±，则称C是U±的一个覆盖，(U±,C)是一个覆盖双向S-粗集.

定义5设(U±,C)是一个覆盖双向S-粗集：

1)x∈U±，x关于(U±,C)的最小描述md(x)进行如下定义：

md(x)={K∈C;x∈K∧∀S∈C(x∈S∧S⊆K→S=K)}.

进而可做出如下定义，md(x)为cv(x)内涉及包含关系的极小元组成的集合，同时

cv(x)={K∈C;x∈K}.

易知，若(U±,R)是一个双向S-粗集，R是U±上的一个等价关系，对于任意x∈U±，记[x]R={y∈U±;(x,y)∈R}为x关于R的等价类，则：

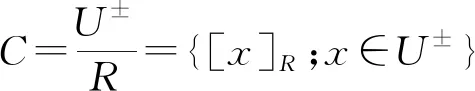
也就是说覆盖双向S-粗集模型是双向S-粗集的推广模型.

2 主要结果

2.1 覆盖双向S-粗集的拓扑

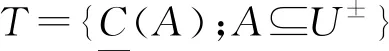
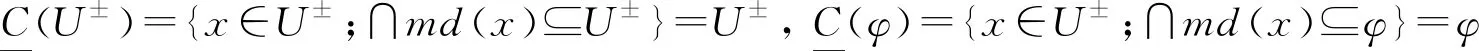
可得U±,φ∈T.

={x∈U±;∩md(x)⊆A}∩{x∈U±;∩md(x)⊆B}

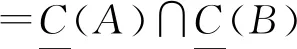
故X,Y∈T时，有X∩Y∈T.

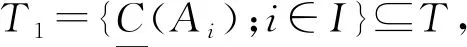
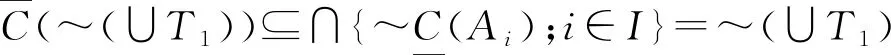
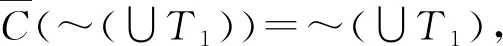
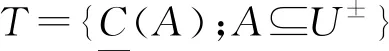
2.2 双向S-粗集的覆盖

引理2设(U±,R)是一个双向S-粗集，此双向S-粗糙集内R属于传递、自反关系，可对CR⊆P(U±)进行下述定义：

CR={RS(x);x∈U±}，那么可将CR视为双向S-粗糙集的1个覆盖，同时针对任意x∈U±，可得∩md(x)=RS(x).

由于R为自反关系，故对于任意x∈U±，x∈RS(x)，则CR组成U±的1个覆盖.针对任意x∈U±，如果K∈md(x)，令K=RS(y)，则x∈RS(y).由此针对任意z∈RS(x)，通过(x,z)∈R且(y,x)∈R，再加上R的传递性，能够明确(y,z)∈R，进而可推导出z∈RS(y)，因此RS(x)⊆RS(y)，如此可确定RS(x)为md(x)内涉及集合包含关系的最小元，故∩md(x)=RS(x).

推论1若(U±,R)是一个双向S-粗糙集，此双向S-粗糙集内，R属于1个自反、传递关系，那么，RCR=R.

推论2假定(U±,C)为一个基于覆盖理论的双向S-粗糙集，针对任意x∈U±，将md(x)以及md′(x)依次记为x关于(U±,C)以及(U±,CRC)的最小描述，那么，md(x)=md′(x).

2.3 覆盖双向S-粗集的部分性质

定理1自反、传递关系下的双向S-粗集与覆盖双向S-粗集是等价的[6].

由引理2及其推论易证.

定理2设(U±,C)是一个覆盖双向S-粗集，则对于任意A⊆U±，有如下关系成立：

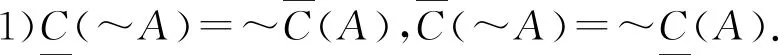
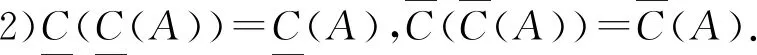
由覆盖双向S-粗集的概念和经典粗糙集的有关性质，不难证明结论成立.

定理3设(U±,C)是1个基于覆盖理论的双向S-粗糙集，对U±上二元关系RC进行下述定义：

针对任意(x,y)∈U±，(x,y)∈RC当且仅当y∈∩md(x)时，RC是U±上的1个传递、自反关系.

如此能够获得如下证明，针对任意x∈U±，关注到x∈∩md(x)，因此，可认为RC是U±上的1个自反关系；针对任意x,y,z∈U±，若(x,y)∈RC，(y,z)∈RC，则y∈∩md(x).如此可理解为，针对任意K∈md(x)，同时再结合y∈K，可发现K1∈md(y)，使得K1⊆K，由此∩md(y)⊆∩md(x).因此，通过z∈∩md(y)能够得到下式：z∈∩md(x)，进而可明确(x,z)∈RC，如此即可判定RC为U±上的1个传递关系.

3 结语

本文主要给出了覆盖双向S-粗糙集模型以及此类模型的部分基本性质.若按照文献[8]的研究思路，进行基于覆盖理论的双向S-粗糙模型的确定增值算子以及不确定增值算子的构建，则同时能够在一定程度上实现对近似算子性质的改进.关于这一问题，我们将另文研究.