大跨度连廊动力响应分析

高 仓

陕西建工第九建设集团有限公司 陕西 榆林 719000

目前国内对于人致振动问题的研究，主要集中于对大跨楼板、人行天桥等结构的振动分析计算方法，人体振动舒适性预测，振动舒适性优化等几个方面[1]。Kerr等[2]总结出步频均值可以选取为1.9 Hz，Matsumoto等[3]获得的步频均值是2.0 Hz，而且服从正态分布。潘宁[4]证实了步行力具有随机性这一现象。马斐[5]、齐曼亦[6]等学者在分析时认为，每个小组中的行人同步频同步调的，可将各组人行荷载曲线施加于结构上进行标准差计算。为减小振动响应，设计时一般采用频率隔离法，这也是我国人行桥规范[7]所采用的方法，结构的跨度越来越大，设计时若考虑使结构的基频远离人的步频，不仅经济性难以满足要求，而且还很有可能发生共振，从而进一步产生由于振动放大效应导致的舒适性问题。

1 工程概况

位于西安火车站（改扩建）东配楼项目中的1幢办公及商业配楼，地裂缝从建筑的左上角方位斜向穿过，把配楼分割成了3个平面极其不规则的建筑单体，如图1所示。为了能够实现建筑功能的连续性，分别在2～5层设置连廊。连廊采用钢桁架结构形式，纵向跨度为45.00 m，横向跨度为9.55 m，由4榀平面桁架组成，每榀之间通过钢梁和斜撑连接形成一个空间桁架结构体系。由于钢连廊的材料特性，容易发生舒适性问题，需系统开展基于人致激励的振动响应计算和减振设计研究。

2 模态分析

结构整体模型如图2所示。选取连廊作为单独结构，建立有限元模型，各杆件截面材料及尺寸如下：上下弦杆采用Q345方钢管，截面尺寸450 mm×300 mm×18 mm× 20 mm；腹杆采用Q345的H型钢，截面尺寸300 mm×250 mm×14 mm×16 mm；钢梁采用Q235的H型钢，截面尺寸300 mm×250 mm×8 mm×10 mm；斜撑采用Q235圆钢管，截面尺寸φ146 mm×6 mm。

图1 结构平面示意

图2 整体模型

为了减少在两侧单体结构发生不均匀沉降时对连廊产生的次生应力，在桁架上弦设置支座，并将左端设置为滑动支座、右端设置为固定铰支座，有限元模型如图3所示。

图3 连廊有限元模型

利用特征向量法对连廊进行模态分析，计算得到前8阶模态。如表1所示。

由各阶模态下周期、频率及质量参与系数可以看出，结构的一阶竖向自振频率为2.5 Hz，在正常人行步频范围之内。当人行步频与结构竖向频率重合或接近时，可能会引起桁架过大的竖向振动，甚至可能导致共振，需定量分析连廊的人致振动响应。

3 动力响应分析

单人步行荷载可以选择Bachmann的单足落步曲线，用来模拟人作为移动荷载时脚步对结构的激励作用。人群荷载可选取的是IABSE[8]中的人行荷载曲线，动荷载因子取前3阶就可较好地反映曲线人群跑动。人的跑动对连廊地面的冲击力曲线按照Bachmann提出的方法，将曲线简化为不连续的半波时程函数。考虑人群同时作用时，不同行人之间的步行力存在相互抵消，此处采用等效人数的方式考虑人群荷载，定义工况如表2所示。

表1 连廊振型周期及质量参与系数

表2 分析工况定义

3.1 单人行走工况

工况1为单人行走工况，连廊的3个通道中，将单人行走荷载以移动点荷载的方式施加于结构上，得到图4所示的加速度时程曲线。

图4 单人行走工况下加速度时程曲线

从图4可以看出，加速度响应在跨中区域最大，当步频为1.25 Hz和2.50 Hz时的加速度时程曲线均呈现出典型的共振状态。在步频为2.50 Hz时加速度响应最大，其原因为步频一阶分量与结构竖向基频接近，形成共振导致加速度不断增大；在步频为1.25 Hz时，其二阶分量虽与结构竖向基频接近，也形成共振，但分量值较小，所以引起的加速度响应也较小。在其他步频激励下，结构加速度响应较为杂乱，呈现无规律性。由表3可以看出，在单人行走工况激励下，结构有较小的加速度响应并且舒适度限值也可以被 满足。

表3 单人行走工况下结构的峰值加速度

3.2 人群连续行走工况

工况2～6为人群连续行走工况，考虑有连续不停的人群通过时对结构的激励，将人群荷载以均布面荷载的方式施加于结构上，得到如图5所示的加速度时程曲线。

图5 人群连续行走工况下加速度时程曲线

由图5可知，在受到周期性人行荷载的作用时，结构响应也呈现周期性变化的特点，加速度随着时间逐渐增大但不是趋于无穷，而是由于阻尼的作用逐渐趋于稳定。

由表4可以得出，加速度峰值曲线在步频为1.25、2.20、2.50 Hz处达到波峰，这是由于步频分量与相应的模态频率相同形成共振导致加速度被放大。在人群连续行走工况下，步频为1.25 Hz时加速度响应峰值仅比2.50 Hz时低3.3%，但在单人行走工况下该数值为73%，产生这种差异的主要原因为等效作用人数的不同，在步频较快时，等效人数较少，步频较慢时等效人数较多。因此，结构的人致振动响应除了激励频率以外，还与作用人数、作用力大小有关。

3.3 跑动工况

工况7为跑动工况，考虑人群跑动通过连廊，这种情况常发生于车站站房等通道中，2.8 Hz跳动工况下加速度时程及频幅曲线如图6所示。

从图6、表5可以看出，所有频率下的加速度峰值响应均满足舒适度评价标准的限值要求，没有出现明显的共振效应。加速度峰值最大为跑动频率2.8 Hz时的0.306 m/s2，相比于人群连续行走2.8 Hz时要大，原因为跑动时人对楼板的作用力比步行时大，所以造成的响应大。

表4 人群连续行走工况下结构的峰值加速度

图6 2.80 Hz跑动工况下加速度时程、频幅曲线

表5 人群跑动工况下结构的峰值加速度

3.4 随机人行工况

连廊上人群的分布位置、行走步频、相位通常是无规律的，针对不同人行走的随机性，结构的人致振动响应情况可以通过概率统计的方法进行分析。

根据Zivanovic的试验结果，得到随机分布的步频和相位，其概率分布如图7所示，可以看到其步频和相位分别符合正态分布和均匀分布的特性，利用步频相位随机数，可以得到84 000条随机人行荷载的样本总体。图8取自样本总体中的1条时程曲线，可以看到曲线仍具有简谐特征，但由于步频和相位在总体中随机取值，典型的荷载时程曲线于此略有不同。

图7 随机步频、相位概率密度分布曲线

将连廊以板块为单位进行分区，每个分区的面积为由四周钢梁所围成的板单元的面积（约为11 m2，共84个分区），每个分区上的人行荷载曲线取自上述随机荷载曲线，每个分区上的人群密度采用JGJ/T 441—2019《建筑楼盖结构振动舒适度技术规范》建议的划分等级，以此来考虑行人分布的随机性，将曲线以面荷载的形式施加于楼板上。这样，每次计算的模型中均存在84个随机人行荷载和随机人群密度，计算1 000次，将计算结果进行统计分析。

如图9所示，随机人行荷载作用下，结构加速度峰值的计算结果类似于正态分布，对加速度峰值进行正态分布拟合，加速度峰值正态分布的均值为0.186 4 m/s2，标准差为0.011 4 m/s2，绝大部分加速度峰值响应落在0.164 0～0.208 8 m/s2的范围内，将随机荷载和确定性荷载作用下的结果进行对比。

由分析可知，在步频为2.50 Hz的确定性荷载激励下，连廊进入共振状态，加速度峰值最大，相比1.25～2.80 Hz的随机性荷载激励，加速度峰值增大约59%，产生这种情况的主要原因是随机人行荷载总体服从正态分布规律，绝大部分步频均在1.87 Hz左右，取到2.50 Hz的概率很小，其荷载分布也不均匀，提取1 000次计算中任意一次的加速度时程和频谱曲线，如图10所示，加速度时程曲线已经没有明显的简谐特征，加速度响应频谱主要分布在1.80～6.80 Hz范围内存在多个峰值，说明该时程响应由多个频率分量组成，其中2.50 Hz分量造成的响应最大，由于其占比较小，引起的加速度较小，而其他频率分量占比较大，但由于偏离了结构竖向基频，引起的加速度也较小，所以总体上造成的加速度响应较小。相比而言，确定性荷载则考虑的是一种最不利情况。需要注意的是，即使随机性荷载产生的加速度峰值响应较小，但绝大部分均超过了舒适度标准0.15 m/s2的限值要求，说明连廊的舒适性有较大概率出现问题。

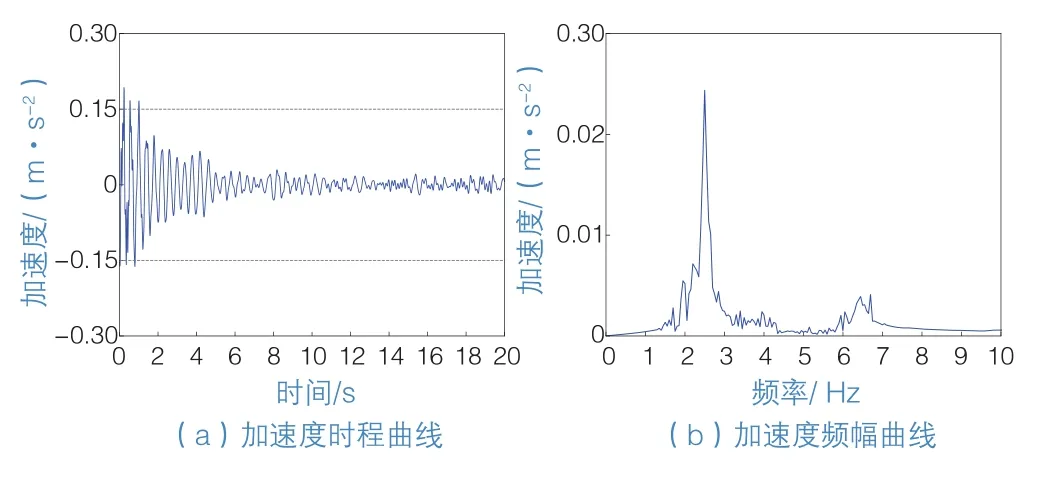
图10 连廊跨中节点加速度时程和频幅曲线

4 结语

根据本文对大跨度连廊进行的动力响应分析，可以得出以下结论：

1）模态分析结果显示，该连廊结构的模态分布较为分散，第一阶竖向振动模态参与质量最大，起控制作用，高阶模态贡献少，竖向基频落入行人正常步频区间，在敏感范围内。

2）连廊动力响应分析结果显示，该连廊结构各工况各步频下的加速度响应最大值均为跨中区域，单人行走、人群连续行走工况下步频为2.50 Hz时，加速度响应达到最大，人群跑动的工况下步频为2.80 Hz，因跑动时人对楼板的作用力比步行时大，所以造成的响应大。

3）人致振动响应的结果显示，确定性荷载作用时，连廊在单人行走、人群跑动的工况下加速度响应满足限值要求，但在人群连续行走工况下，步频与结构竖向基频共振时响应值较大，超过舒适度标准的要求，随机性荷载作用时也表明连廊有较大概率存在舒适性问题，在不改变结构形式的情况下需要进行减振控制。