基于逐步回归方法下400米决赛成绩的分析研究

潘 丹，熊江媛

(1.湖北师范大学 体育学院，湖北 黄石 435002；2.华南师范大学 体育科学学院，广东 广州 510631)

0 引言

2019年世界田径锦标赛于2019年9月27日至10月26日在卡塔尔首都多哈举行，世界田径锦标赛每两年举办一次，除了奥林匹克运动会以外，它是国际上最高级的田径赛事，汇集了来自世界上能够代表各个国家最高水平的田径运动员，这些高水平运动员之间相互较量，能很大程度上反映出当今各个田径项目的发展特点和趋势。本文对男子400米决赛八名运动员的各段成绩进行研究，试图展示400米项目的发展趋向，从而精准地把握400米的训练方向，在借鉴国外有效训练方法的基础上为提高我国男子400米跑的成绩提供理论依据[1～3]。当今中国短跑项目已经发展到能与欧美各个国家相媲美，所以研究世界高水平短跑运动员的成绩对我国有借鉴意义。

400米跑的各段成绩也是研究400米跑能力的依据，大部分学者对400米分段成绩的研究是从100米、200米角度研究的，近年来有不少文献资料已经证明了我国短跑项目在起跑后的30～50米名列前茅，只有较少一部分学者提出研究50米分段成绩对于提高运动员的400米成绩具有重要作用，但并未结合我国短跑项目的优势，研究出哪几段50米与400米成绩非常相关。因此，为了使我国400米运动员的比赛成绩有所提高，本文在结合我国短跑优势的基础上以2019年世界田径锦标赛男子400米决赛成绩为研究对象，以50米为一段，整理相关数据，并对相关数据进行逐步回归分析，剖析出哪几段50米与400米成绩呈显著相关，建立回归模型，为我国400米项目的训练提供更加科学的指导。

1 研究对象及方法

1.1 研究对象

本文以2019年多哈田径世界锦标赛男子400米决赛八名运动员在全程中各50米分段速度成绩为对象建立模型组，包括第二道布鲁姆费尔德(BLOOM FIELD)、第三道盖伊(DEMISH GAYE)、第四道史蒂文加德纳(STEVEN GARDINER)、第五道弗雷德克利(FRED KERLEY)、第六道马谢尔塞多尼奥(MACHEL CEDENIO)、第七道基拉里詹姆斯(KIRANI JAMES)、第八道安东尼乔斯扎姆布拉默(ANTHONY JOSE ZAMBRANO)、第九道科里尔(KORIR)。

1.2 研究方法

1.2.1 文献资料法 在中国知网上检索了有关“短跑成绩研究”“田径400m”“田径400米”“400m运动成绩分段研究”为关键词的相关期刊、硕博士论文以及与其相关的文章，根据在中国知网查阅关于400米分段研究的文献资料，大多数学者选取影响400米成绩的自变量为100米、200米、300米，较少学者选取50米为自变量进行分析，探讨每段50米与400米成绩的影响。因此本文将2019年世界田径锦标赛男子400米决赛八名运动员的成绩划分为八个单独的50米作为自变量，并运用一元线性回归方程、二元线性回归方程及逐步回归方程对第八段50米和第六段50米进行比较与分析。

1.2.2 视频解析法 在CCTV5体育赛事频道官方网站上对2019年世界田径锦标赛男子400m决赛视频进行下载，视频通过格式工厂转换为AVIH格式后导入KINOVEA软件，利用软件对视频进行剪辑与保存，将保存的视频逐帧播放进行统计，利用DARTFISH软件对视频反复播放，将2019年世界田径锦标赛男子400米决赛八名运动员的成绩划分为八个单独的50米。通过视频软件中显示的时间对各段50米的距离时间数据收集，同时结合国际田联官网上关于2019年多哈世界田径锦标赛男子400米决赛的其他相关统计数据，为本文提供数据支持。

1.2.3 数理统计法 借助Excel软件，对搜集的各个数据进行分类处理，统计分析，为本文提供数理支持。对照组成绩数据以均数±标准差表示，运用两独立样本t检验分析，若P<0.05则表示显著性差异，P<0.01则表示高度显著性差异。

数据来源于国际田联官网上关于2019年多哈世界田径锦标赛男子400米决赛的相关统计数据。每一道次代表每名运动员，400米成绩用y/s表示，第一段50米用x1/s表示、第二段50米成绩用x2/s表示、第三段50米成绩用x3/s表示、第四段50米成绩用x4/s表示，第五段50米成绩用x5/s表示，第六段50米成绩用x6/s表示，第七段50米成绩用x7/s表示，第八段50米成绩用x8/s表示。如表 1所示。

表1 400米成绩回归自变量

2 结果与分析

2.1 自变量“第八段50米”预测400米一元线性回归方程

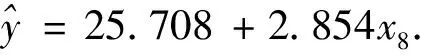
表2 第八段50米预测400米一元线性回归方程方差分析表

经方差分析F=36.068，P<0.01，回归方程非常显著。第八段50米预测400米一元线性回归方程的剩余标准差为0.259s.

2.2 自变量“第六段50米”预测400米一元线性回归方程

表3 第六段50米预测400米一元线性回归方程方差分析表

经方差分析F=29.501，P<0.01，回归方程非常显著。第六段50米预测400米一元线性回归方程的剩余标准差为0.282秒。

2.3 自变量“第八段50米”“第六段50米”预测400米二元线性回归方程

表4 二元线性回归方程方差分析表

2.4 400米成绩自变量逐步回归分析

1)运用正交筛选法对Pearson相关又称之为简单相关系数R(0)选择第一个自变量进入方程，计算其偏回归平方和：

2)选择第二个自变量进入回归方程，计算偏回归平方和:

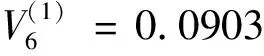
F=(8-3)×0.0903/(0.1425-0.0903)=8.6494>Fα=6.59,故自变量x6作用显著，引入回归方程中，对R(1)变换得R(2).

3)选择第三个自变量进入回归方程，计算偏回归平方和：

F=(8-4)×0.0436/(0.0522-0.0436)=20.2791>Fα=6.59，自变量x1作用显著，引入回归方程中，并对R(2)变换得R(3).

4)判断是否应该从回归方程中剔除变量，对已选入的自变量x8、x6、x1，计算他们的偏回归平方和。

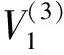
5)引入第四个自变量，对剩余的自变量x2、x3、x4、x5、x7，计算它们的偏回归平方和。

F=0.0057×(8-5)/0.0085-0.0057=6.1071

表5 逐步回归方程方差分析表

2.5 一元线性回归方程、二元线性回归方程、逐步回归方程模型预测400米成绩比较结果

根据上述逐步回归计算过程所得到的回归方程，对2019年世界田径锦标赛男子400米决赛实际成绩数据(44.6686±0.4232)和回归方程预测成绩数据进行比较(44.6571±1.6998)。四个模型所预测的成绩和实际比赛成绩之间的相关系数P<0.01，表明模型预测成绩和实际成绩两者之间有非常显著的差异。

四个模型所预测的成绩和实际比赛成绩之间的配对t检验的结果是P>0.05，这说明模型预测成绩和实际成绩之间没有明显的显著性差异，由此可见四个模型预测400米成绩的实际效果较好。

逐步回归方程预测成绩与实际比赛成绩之间的一致性相关系数0.9357最高，逐步回归方程剩余标准差0.078s最小，这说明所建立的方程预测效果好、准确性高[4]。四种回归方程模型预测400米能力的对比研究见表6.

表6 四种回归方程模型预测400米能力的对比研究

2.6 逐步回归分析结果的理论依据

400米第一个分段是起跑后的50米，这一阶段和400米比赛中的最后冲刺阶段同等关键。起跑所需要的成绩对总成绩的影响有着举足轻重的作用，起跑时快速反应的能力可以使运动员在比赛中获得有利速度的发挥身位[5]。因此，依据逐步回归分析的结果，起跑这一阶段在400米训练中的重要作用也就显而易见地表现出来。400米第六个分段是进入最后冲刺阶段的关键所在。运动员跑完弯道所需时间要比跑完直道所用时间要多体力消耗更大，因此如果能有效地改善运动员的弯道跑技术，在训练中加以强化，这样运动员在弯道跑上所节省出来的部分时间，将会对短跑类项目的总成绩有很大的帮助[6]。在400米弯道加速过程中,有效地运用弯道跑技术,是获得优秀400米成绩的重要因素之一[7]。因此，综合前文逐步回归分析结果的基础上，第六段50米即最后弯道对400米成绩的影响是至关重要的。400米第八个分段是冲刺跑最后50米，这一阶段通常是影响400米成绩的决定性因素。所以一直以来, 400米的运动员、教练员和体育科研人员都非常重视运动员最后冲刺能力的培养, 长期探索各种有效的训练方法和手段，为提高运动员的速度耐力及骨骼肌的抗乳酸能力,通过不断地训练来提高400米运动员的比赛成绩[8]。

3 结论