填芯与非填芯管桩纵向振动特性数值模拟对比
2020-12-01郝屹峰张毅磊唐小雨范一丁
郝屹峰,张毅磊,唐小雨,范一丁
(苏州科技大学 土木工程学院,江苏 苏州 215011)
0 前 言
在工程中,填芯管桩在非填芯管桩的基础上利用桩芯中空的特点,采用填芯工艺对管桩进行处理,使原有管桩力学性能满足实际应用需求。与单纯的管桩相比填芯处理增大桩体刚度、提高管桩性能,与实体桩比较则更加经济,具有广阔的应用前景。
在桩基纵向振动数值研究方面,早在20世纪70年代,Blaney[1]、Banerjee等[2]就分别开始利用轴对称有限元法和边界元法对桩基的纵向振动问题进行分析;Angelides等[3]采用非线性的有限元程序开展了桩土振动特性的研究;Sen等[4]基于边界元法,考虑非均质土在纵向动力荷载条件下对单桩、群桩动力特性进行研究;Y K Chow 等[5]通过有限元程序编写建立桩-土数值模型,来分析桩土间动力响应问题。随着计算机技术的成熟,涌现许多实用的数值软件。季勇志[6]采用ANSYS软件对码头桩基进行模拟并与实测曲线对比,进一步验证软件在桩基检测方面的可靠性。
在填芯管桩研究方面,李悦等[7]对不同填芯材料的PHC管桩参数进行静力试验,并分析了抗震性能的影响;吴声扬[8]利用管腔中空对大直径随钻跟管桩进行填芯处理增大桩体刚度,对不同工况填芯的长度、强度进行了试验和数值分析。总之,填芯管桩的工程应用逐渐增多相关静力学研究给实际工程提供了不少理论支撑,但在动力学方面特别是纵向振动问题上,填芯管桩与非填芯管桩的动力特性对比研究较少。因此,本文结合ANSYS数值模型对不同参数的填芯管桩和非填芯管桩的桩顶速度时域响应曲线进行对比分析。
1 (非)填芯管桩数值模型建立及相关参数设置
1.1 数值模型建立
基于ANSYS17.0建立(非)填芯管桩-非均质土模型,考虑到桩周土体径向非均匀和纵向成层性,建立桩土圆柱体模型因圆柱体模型的对称性,同时也为了减少模拟时的计算量,采用LS-DYNA程序建立1/4(非)填芯管桩-土结构体模型,针对该模型系统选用SOLID185,即三维8结点结构实体(在节的X,Y,Z方向可以模拟可塑、超弹性、应力加劲、蠕变以及弹塑性体等相关材料),图1为模型及网格划分。
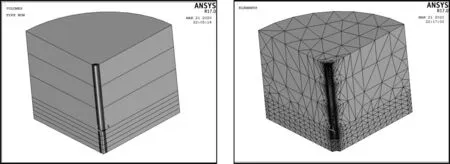
图1 1/4非填芯管桩-土模型
由于桩顶激振力Q(t)较小,将桩体本身、桩侧土体以及桩端土体均看作线弹性变化,作低应变问题处理。(非)填芯管桩-土系统在耦合振动时将对应的桩侧土体和桩身视为位移连续,在模型中采用VGLUE将整个系统各个接触面粘结成一个整体,以保证网格化后,各部分几何体相关接触面上的节点应力应变变化一致。在精度方面采用h-method,通过减小单元尺寸加密网格划分来提高精度,使有限元模拟在后续求解计算时结果更为精确。
1.2 模型参数设置
本模型将(非)填芯管桩置于桩周土体几何中心,在施加脉冲前对模型初始条件及约束条件进行定义,考虑土体径向非均质内部圈层区域(近桩)设为5层每层0.1 m,外部区域(远桩)半径为20 m。因(非)填芯管桩在土体中仅发生纵向位移(径向位移忽略),需对桩底土进行约束,桩端(含虚土桩)土体以及桩侧土体外表面定义为无反射边界条件。桩顶则采用均布荷载形式,考虑低应变问题,故在桩顶面的节点组元上施加半正弦脉冲,如图2所示。
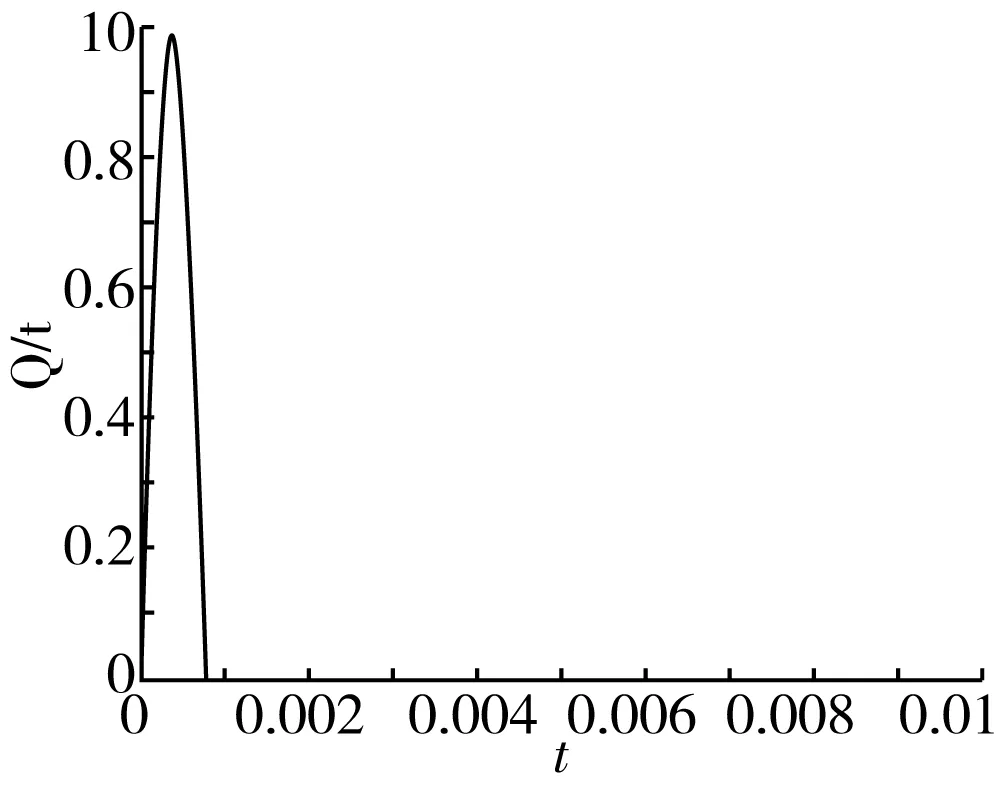
图2 半正弦脉冲图
2 填芯管桩与非填芯管桩顶动力响应数值计算
2.1 非填芯管桩与不同填芯剪切波速的填芯管桩桩顶动力响应对比
建立土体非均质数值模型,管桩内径0.2 m,外径0.3 m,桩长为12 m,填芯高度取5 m,土塞高度取2 m,其他参数如表1所示。
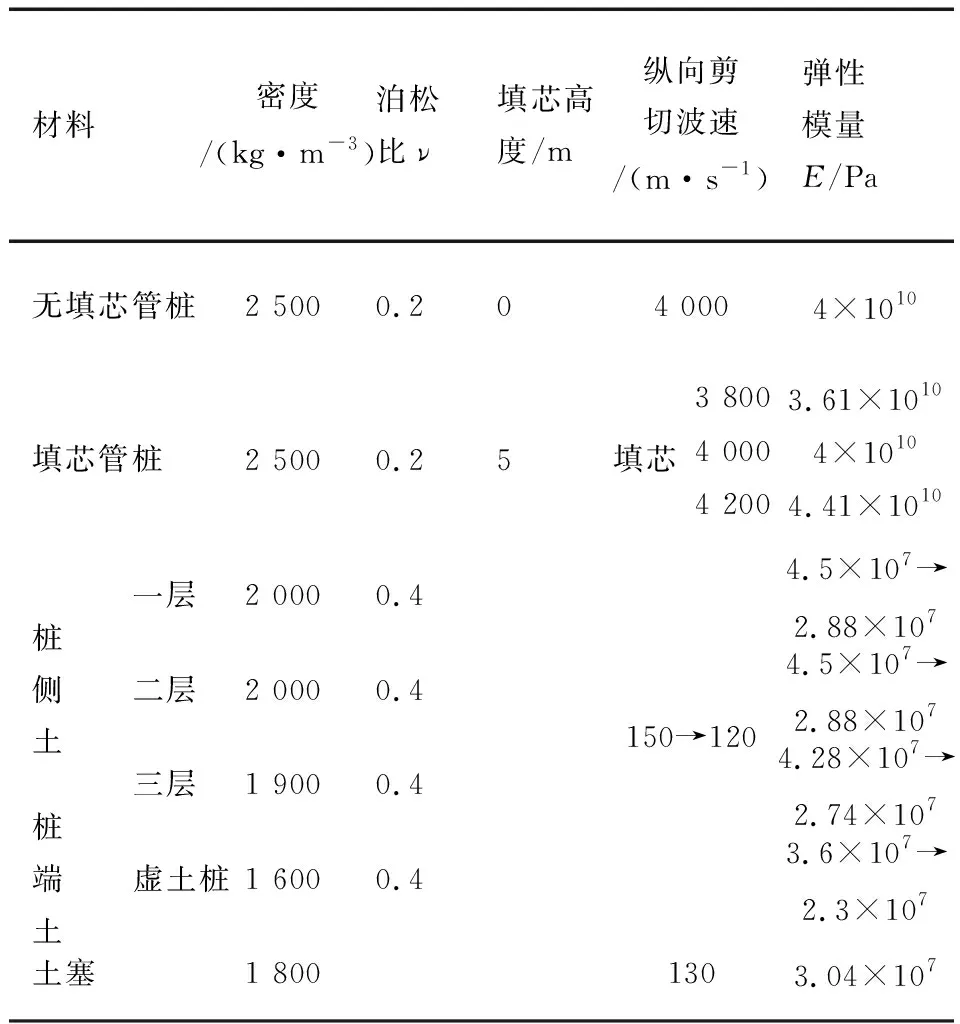
表1 (非)填芯管桩土相关参数(填芯纵向剪切波速)
将非填芯管桩与不同填芯剪切波速的填芯管桩分别进行对比见图3。
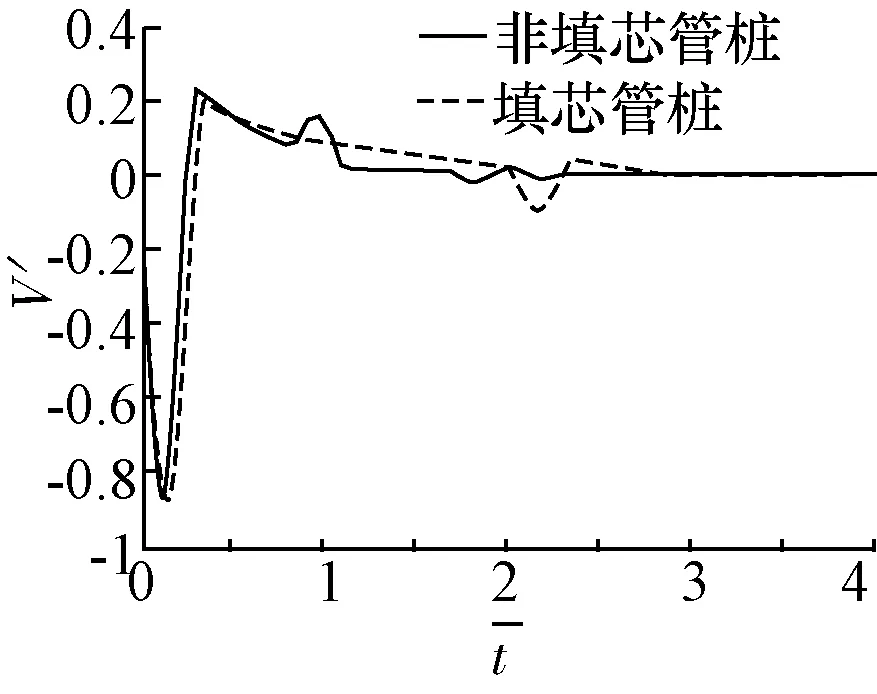
(a)填芯Vt=3800 m/s
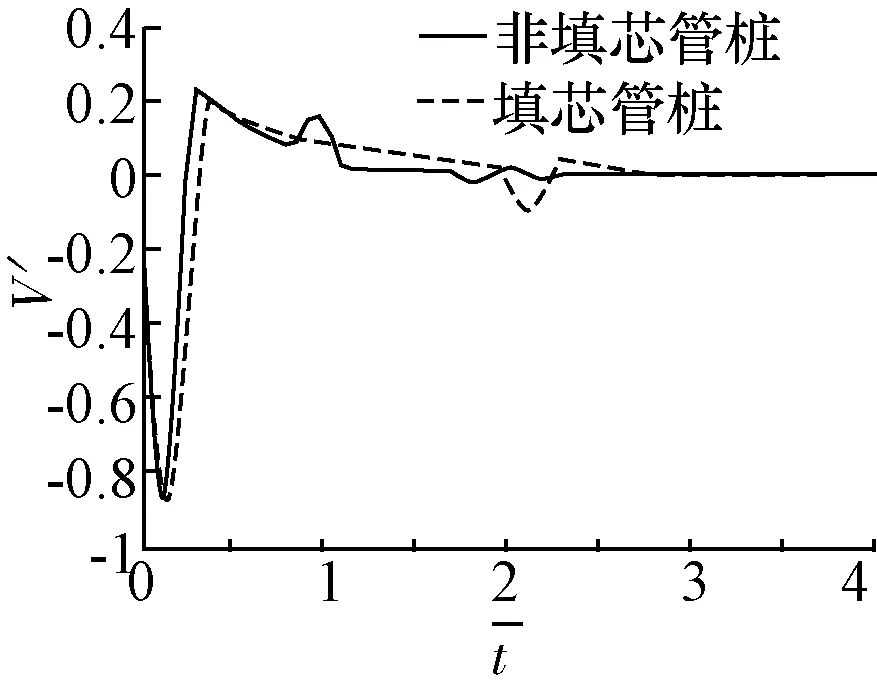
(b)填芯Vt=4000 m/s
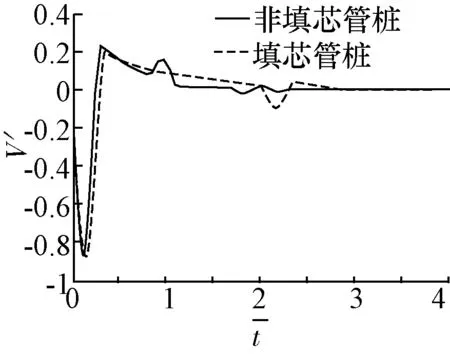
(c)填芯Vt=4200 m/s图3 (非)填芯管桩桩顶速度时域响应数值解对比(填芯剪切波速)
由图3可知,当填芯剪切波速不同各段曲线区别较小,总体来说非填芯管桩与填芯管桩之间在结构上的差异性在桩顶时域响应曲线可以反映出来,由于填芯的存在使曲线在同向反射后会产生一个较明显的反射后面围绕稳定值上下浮动振幅呈减小趋势,说明填芯使管桩的整体力学性质变好,使桩顶时域响应曲线反射明显,且相对非填芯管桩而言信号明显提前,能量消散较快。
2.2 非填芯管桩与不同填芯高度的填芯管桩与桩顶动力响应对比
除了填芯剪切波速之外,填芯高度对管桩本身也会产生影响,本文结合数值模型进行非填芯管桩与填芯管桩与桩顶速度时域响应对比分析。建立内径0.1 m,外径0.3 m,桩长12 m的数值模型,桩端土厚度取5 m,不考虑土塞效应,其他相关参数如表2所示。
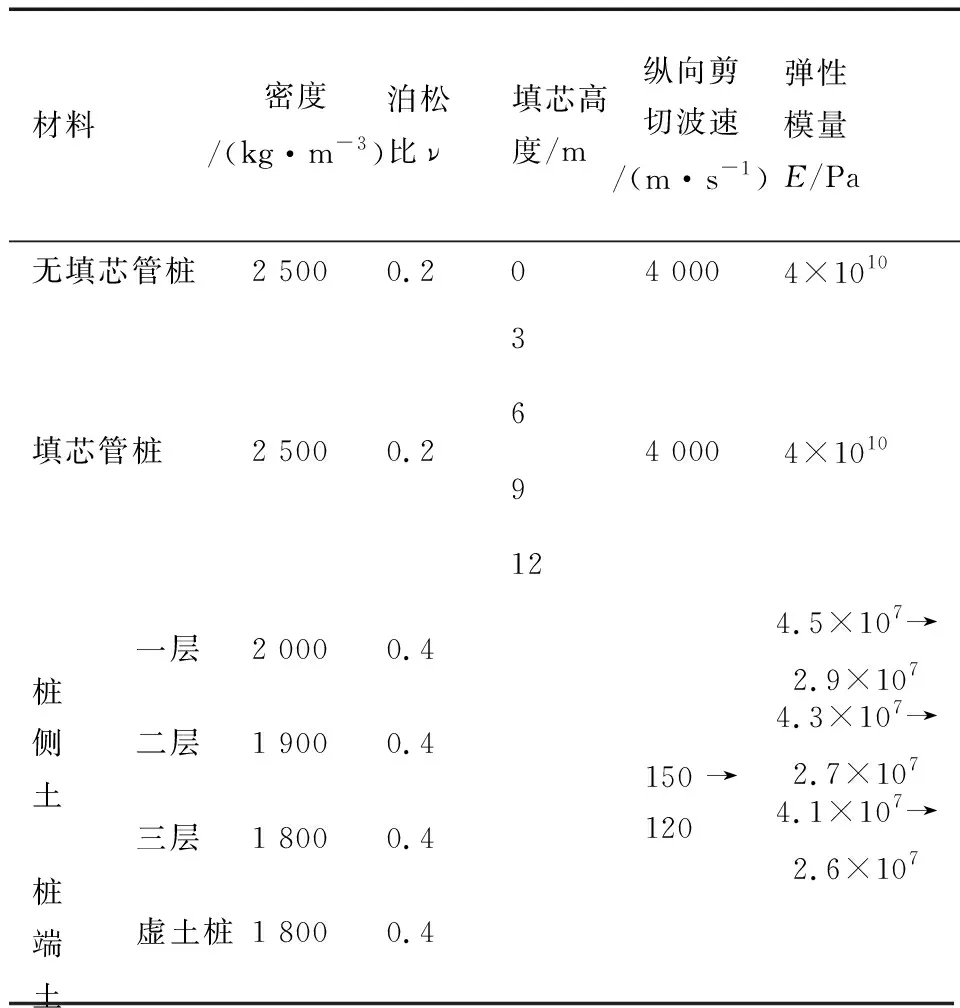
表2 (非)填芯管桩土相关参数(填芯高度)
图4为非填芯管桩分别与不同填芯高度填芯管桩数值解对比,当填芯为12 m时,管桩腔体内均被填满可近似为实心桩,通过二者之间桩顶速度时域响应数值解对比可知,随着填芯高度的变化曲线产生不同程度的变化,总体来说与非填芯管桩的桩顶时域曲线呈现较明显区别,具体表现为填芯之后同向峰值明显增大,反向峰值略微减小,信号减小所消耗时间短等特点。
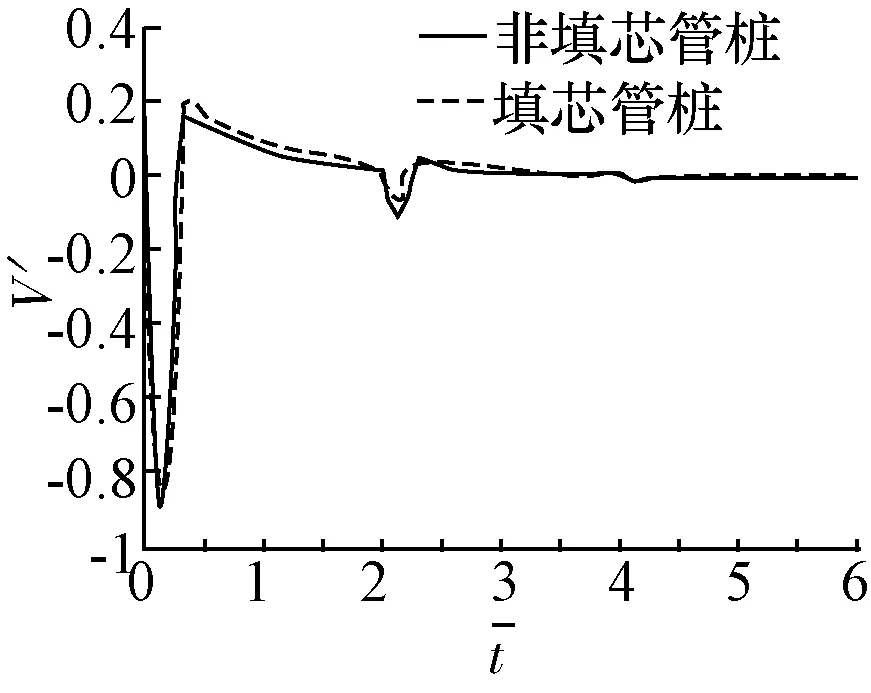
(a)填芯3 m
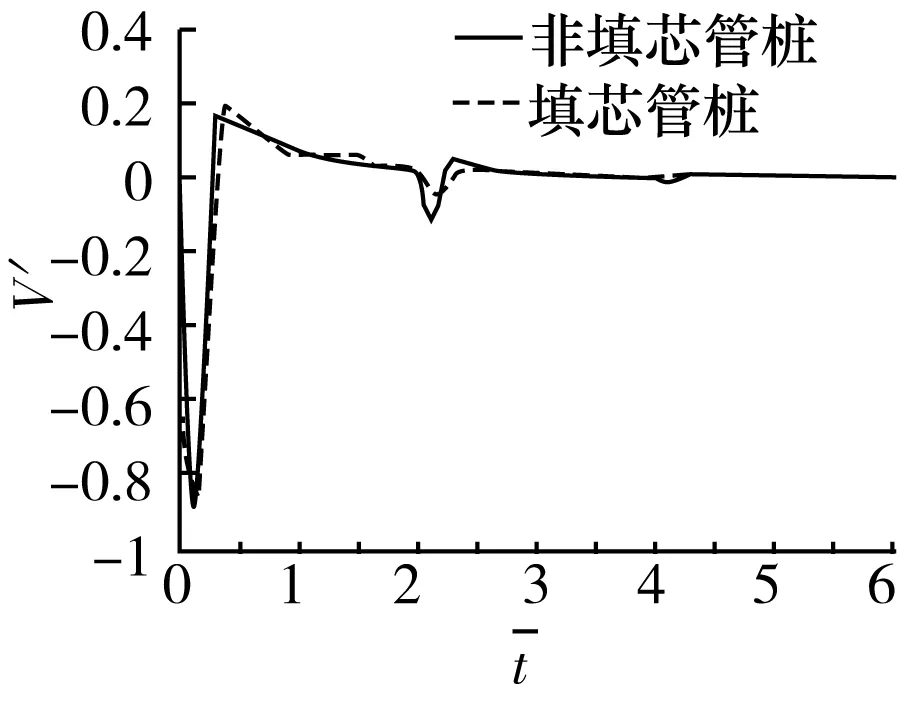
(b)填芯6 m
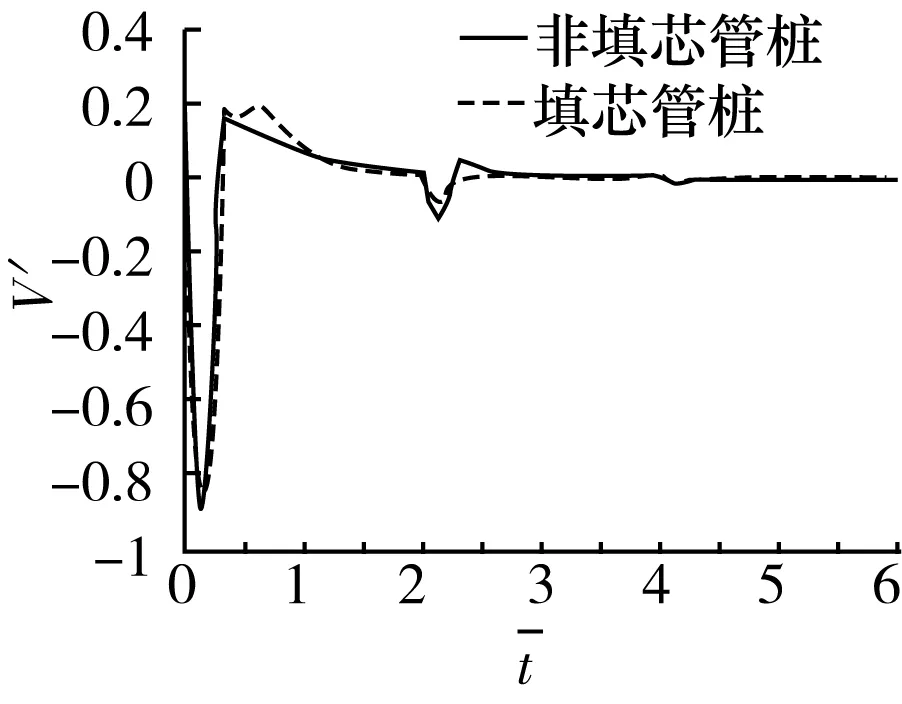
(c)填芯9 m
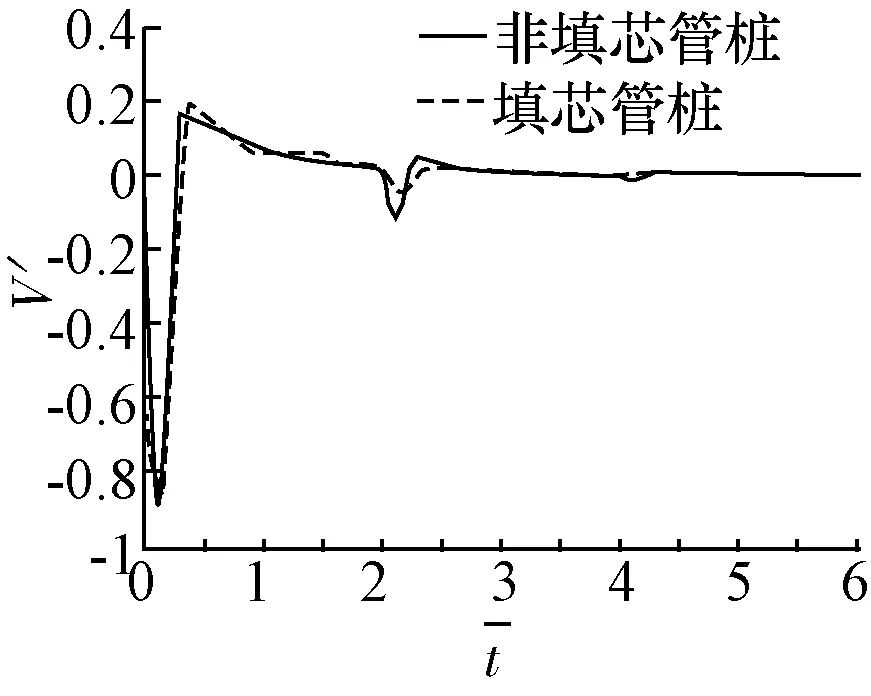
(d)填芯12 m图4 (非)填芯管桩桩顶速度时域响应数值解对比(填芯高度)
3 结 论
1)非填芯管桩与不同填芯剪切波速的填芯管桩进行对比,当填芯剪切波速不同各段曲线区别较小,非填芯管桩与填芯管桩之间在结构上存在差异,但填芯的存在使曲线在同向反射后会产生一个较明显的反射,相对非填芯管桩而言信号明显提前,说明填芯使管桩的整体力学性质变好。
2)非填芯管桩与不同填芯高度的填芯管桩对比,随着填芯高度的变化曲线产生不同程度的变化,总体来说与非填芯管桩的桩顶时域曲线呈现较明显区别,具体表现为填芯之后同向峰值明显增大,反向峰值略微减小,信号减小所消耗时间段等特点。
[ID:010444]
