西藏普兰地区第四纪以来冰锯作用研究

郭浩 刘耕年

西藏普兰地区第四纪以来冰锯作用研究

郭浩 刘耕年†

北京大学城市与环境学院, 北京 100871; †通信作者, E-mail: liugn@pku.edu.cn

为了验证西藏普兰地区冰川作用对地形演化的影响, 选取纳木那尼峰、喜马拉雅山和冈底斯山 3 个区域, 利用数字高程模型(DEM)数据和遥感影像, 对现代冰川与末次冰盛期(LGM)古冰川平衡线高度(ELA)、冰川作用区坡度与高程的关系以及冰川分布的高程频谱进行计算和分析。结果显示, 研究区内冰川剥蚀作用显著、坡度降低最明显的地带位于 LGM 古冰川平衡线附近, 并在一定程度上限制山脉的高度。根据冰川地貌特征参数和前人研究结果, 认为气候是影响冰锯作用的主要因素。冰期时, 研究区内西风急流南移, 风速增强, 降水量增多, 为冰川发育创造良好条件, 冰锯作用也增强。对于构造抬升强烈的山脉(如纳木那尼峰), 虽然冰锯作用得到加强, 但是构造抬升增加的山脉高度不会完全被冰锯作用抵消。

冰锯; 平衡线高度(ELA); 海拔; 坡度; 构造抬升; 气候

气候、构造和地形三者的关系一直是地貌学研究的焦点。地形的演化由抬升、剥蚀、堆积和沉降作用耦合控制, 其中, 抬升主要受构造驱动, 剥蚀则包含各种形式的风化、侵蚀和块体运动[1‒2]。纵观全球, 剥蚀主要受流水作用和坡度控制。然而, 对于山地及中高纬度环境, 冰川过程可能在地形塑造中起着主导作用[3]。冰川剥蚀主要通过冰下侵蚀的方式进行, 包括磨蚀、拔蚀、冰下流水作用等[4], 其强度取决于冰川移动速度、冰川厚度、冰下水压和基岩性质等因素。总体来说, 冰下侵蚀在总冰流及冰下滑动速率最大的地方最强[5--6]。对于多数冰川, 侵蚀作用最强地带往往在冰川平衡线附近[6‒7]。冰川平衡线的海拔高度受很多局地因素影响, 如地形遮蔽程度和雪崩等[8], 但从区域尺度看, 主要受气温和降水等气候因素控制[9]。在平衡线之上, 谷坡与冰斗后壁侵蚀加剧, 地形梯度增加, 山峰的海拔也受到限制[10‒11]。在平衡线之下, 冰流及滑动速率的减少导致冰川侵蚀作用减弱, 冰川沉积物的堆积也阻碍冰后期的流水侵蚀[12]。平衡线附近的侵蚀与沉积特征共同导致平衡线处出现“冰锯地形”。冰锯地形的特征包括集中分布在古冰川平衡线附近以及山峰的海拔高度与古冰川平衡线高度之间显著的相关性等[2‒3,11,13‒15]。

冰锯理论认为冰川侵蚀作用倾向于将冰川作用区之上的山地剥蚀、夷平, 起到限制山地高度的作用, 最强烈的“锯平”带位于冰川平衡线位置(高度), 由于冰期、间冰期交替, 锯平带位于冰期与间冰期平衡线之间[3]。这个假说认为高大的山脉倾向于被夷平至冰川平衡线高度, 平衡线起到“气候基准面” (climatic base level)的作用[13]。

有关冰锯作用塑造山地地形的研究为数不少。继 Brozović 等[13]研究喜马拉雅山西北区域的山地构造变形, 首先指出冰锯作用在山地地形塑造中的意义以来, 学者们纷纷证实这种作用的普遍性, 如对北美山地[2,11,14,16‒17]、南美山地[18]、欧洲阿尔卑斯山[19]以及全球尺度[3,15]的研究。但是, 也有研究者发现冰锯作用的例外情况, 原因与构造运动和岩石抗侵蚀强度有关[14,17‒18], 也可能由于冰期冷的冰川底部几乎不滑动导致冰川侵蚀作用弱[18]。阿拉斯加山脉高耸在冰川平衡线之上, 边坡陡峻, 几乎没有冰雪覆盖, 被称为“特氟龙峰(Teflon peaks)”[17], 这种山地景观的形成可能是受岩性的影响。另有研究者发现, 在喜马拉雅山脉的高山脊上, 冰川的侵蚀作用反而削弱, 这是因为低温极大地限制了冰斗后壁的冻裂, 避免冰锯作用, 保护了高大分水岭[20]。

Brozović等[13]在对青藏高原西北部的研究中指出气候对冰锯作用的影响, 末次冰盛期(last glacial maximum, LGM)的冰川平衡线高度(equilibrium line altitude, ELA)比现代低 600~1000m, 第四纪冰川的平均 ELA 比现代低 400~500m, 冰川平衡线的降低直接导致冰川积累区面积增大, 增加冰川通量, 加快冰川的侵蚀速率。在 Nanga Parbat 北坡, 冰川覆盖区的现代侵蚀速率为 4.6~6.9mm/a, 而非冰川覆盖区则为 1.4~2.1mm/a。冰锯作用导致山体海拔受限制, 以 Nanga Parbat 为例, 虽然其顶峰海拔超过8000m, 但平均海拔仅 4800m。

为了进一步探究青藏高原及周边山地的冰锯作用, 本文选取位于青藏高原西北缘的西藏阿里普兰地区(比 Brozović 等[13]的研究区更靠南)作为研究对象。该区与尼泊尔、印度接壤, 区域内部的冈底斯山、阿伊拉日居山、喜马拉雅山脉发育现代冰川, 古冰川遗迹广泛分布, 是揭示藏西北高原演化的关键部位(图 1)。普兰地区的北端是冈底斯山脉, 南端是喜马拉雅山脉, 处于强烈抬升与剥蚀过程中, 其中纳木那尼峰在地质构造上属于相对独立的韧性拆离体[21], 发育现代冰川和第四纪冰川[22‒26]。一直以来, 对该区域第四纪冰川和地貌的研究相对薄弱。本文选取喜马拉雅山脉西缘一段(大致范围为80°—81°E)、纳木那尼峰和冈底斯山 3 段山脉, 研究其地形演化与冰川作用的关系。

1 研究区概况

1.1 区域气候概况

研究区位于西藏普兰地区。如图 1 所示, 喜马拉雅山脉和冈底斯山脉北西‒南东向排列, 纳木那尼峰位于东南角, 狮泉河、象泉河和孔雀河发源于该区域。研究区内大部分地区海拔大于 4500m, 年均气温≤0℃, 地势较低的河谷年均气温为 5~10℃。干旱少雨, 年降水量为 100~200mm, 属于高寒干旱大陆性气候。普兰盆地具有山地灌丛草原景观, 年均气温为 3℃, 极端最高气温为 26.5℃, 极端最低气温为−27.5℃。冬半年受西风带南支气流控制, 干燥晴朗; 夏半年西风带南支北跳, 印度季风进入, 补给一定的水汽, 年降水量为 189.6mm, 40%的降水集中在8月。

1.2 区域地质概况

冈底斯山脉主峰为冈仁波齐峰, 海拔 6638m, 是由第四纪冰川侵蚀作用形成的金字塔形角峰, 山体的岩性为砾岩[27]。札达盆地与噶尔盆地之间的阿伊拉日居(拉日神山)发育现代冰川, 第四纪冰期冰进的遗迹也十分丰富。朱大纲等[28‒29]确认沟谷和山麓地带有四套冰川沉积物。札达盆地河湖相沉积及其揭示的晚新生代区域环境变化[30‒31]受到学界关注。

纳木那尼峰(Gurla Mandhata, 峰顶海拔 7694m)在地质构造上属于韧性拆离体[21], 发育现代冰川和第四纪冰川, 区域内有著名的喀喇昆仑断裂穿过。喀喇昆仑断裂是青藏高原西部最重要、最活跃的断裂, 控制着区域地形[32‒34]。纳木那尼峰地区共有现代冰川 58 条, 面积为 80.93km2。冰川大体上以纳木那尼峰为中心向四周放射状扩散, 主山脊北侧有7 条山谷冰川, 聚集了该地区绝大部分冰量, 约占总量的 70%以上, 山体的南侧则全部为悬冰川。

喜马拉雅山脉西起南迦巴特峰, 东至南迦巴瓦峰, 长逾 2500km; 北以雅鲁藏布江‒狮泉河为界, 南界为印度恒河平原北侧边界的主前缘断层[35], 宽 200~300km; 大体呈向南凸出的弧形, 平均海拔在 5000m 以上, 山脉南侧海拔较低, 平均 2500~4500m, 北侧较高(>5000 m)[36]。喜马拉雅主碰撞带位于印度‒雅鲁藏布江缝合带与喜马拉雅主前锋冲断裂之间, 自北往南为特提斯喜马拉雅岩片、高喜马拉雅岩片、低喜马拉雅岩片和次喜马拉雅岩片[37]。

2 数据与研究方法

2.1 数据来源

现代冰川数据来源于中国科学院国家青藏高原科学数据中心《中国第二次冰川编目数据集(V1.0) (2006—2011)》[38]; 数字高程模型(digital elevation model, DEM)数据来源于中国科学院计算机网络信息中心地理空间数据云平台(http://www.gscloud. cn), 利用 ASTER GDEM 第一版本(V1)的数据加工得来, 空间分辨率为 30m; LGM 古冰川分布范围是在 Owen 等[24]的基础上, 通过 Google Earth 遥感影像解译而来。

2.2 研究方法

1)研究区划分。本文研究区划分为喜马拉雅山、纳木那尼峰和冈底斯山 3 个区域, 区域边界由分水岭和谷地组成。

2)坡度‒海拔分布。根据分辨率为 30m 的 DEM图, 利用 ArcGIS 的空间分析功能, 计算研究区每个栅格的坡度。采用 Hergarten 等[39]的方法, 分析研究区坡度‒海拔的分布情况。除考虑某个海拔段对应坡度的平均值外, 还要考虑海拔段坡度的分布情况[40]。以 50m 高度为间隔, 将研究区的坡度‒海拔数据集分成若干子集, 在各子集内部计算坡度值的平均数和中位数。最后, 以各子集的平均海拔为自变量, 以各子集坡度的平均值和中位数为因变量, 绘制坡度‒海拔关系图。

3)计算冰川平衡线高度。结合冰川编目数据和卫星影像分析, 剔除最高海拔低于分水岭且面积小于 10000m2的冰川, 用冰川末端‒冰斗后壁比率法(toe-to-headwall altitude ratio, THAR)计算 ELA 值[41‒42], 冰川 THAR 值取0.5[43]。

4)绘制冰川分布的高程频谱。根据分辨率为30m 的 DEM 数据, 分别提取 3 个区域的海拔高度, 分成 100 个区间, 制成冰川分布高程频谱图。

5)绘制坡度频谱。用现代冰川和 LGM 古冰川的 ELA 数据进行海拔分段, 将 3 个区域的 LGM 古冰川分成 3 段: 高于现代冰川平衡线, 现代冰川平衡线与 LGM 古冰川平衡线之间, 低于 LGM 古冰川平衡线。提取 3 段的坡度数据, 制成冰川分布坡度频谱图。

3 结果

3.1 冰川平衡线高度

用 THAR 法计算 3 个区域内每条现代冰川的ELA, 统计结果见表 1 和图 2。喜马拉雅山 ELA 值最低, 为 5703m; 冈底斯山次之, 为 5817m; 纳木那尼峰 ELA 值最高, 为 5955m。冈底斯山 ELA 的标准差最小, 说明 ELA 值的分布最为集中; 纳木那尼峰和喜马拉雅山的 ELA 标准差均超过 200m, 说明 ELA 值的分布较为分散。

用 THAR 法计算 3 个区域内每条 LGM 古冰川的 ELA 值, 统计结果如图 2 所示。喜马拉雅山的ELA 值最低, 为 5350 m; 冈底斯山次之, 为 5400 m;纳木那尼峰 ELA 值最高, 为 5486 m。

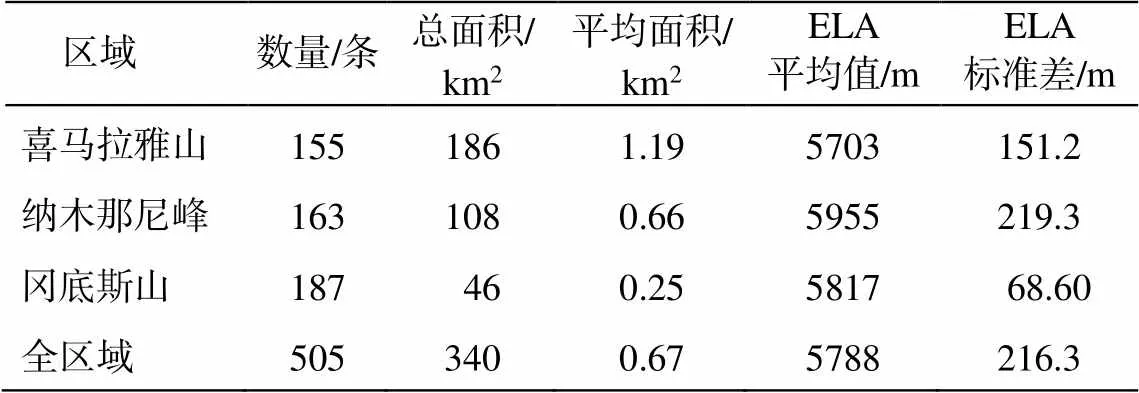
表1 研究区现代冰川信息统计

3.2 冰川分布高程频谱

将喜马拉雅山、纳木那尼峰和冈底斯山 3 个区域冰川分布的海拔数据制成高程频谱(图 3)。

从冰川分布的海拔高度范围来看, 喜马拉雅山冰川在各海拔高度区间的分布较为均匀, 4800~5700 m 范围内的分布频率均在 10%左右; 冈底斯山和纳木那尼峰冰川在各高程区间的分布频率有明显的峰值, 冈底斯山以 5600m 为基准, 纳木那尼峰以 5700m 为基准, 向上向下的分布频率均呈指数级衰减。

从冰川分布的集中程度来看, 喜马拉雅山冰川主要分布在 4800~5000m 和 5200~5600m 两个高程区间, 冈底斯山和纳木那尼峰冰川分布的主要高程区间分别为 5400~5800m 和 5500~5900m。

从冰川分布的高程跨度看, 纳木那尼峰的冰川分布在 5200~7681m , 高程范围最广, 跨度达 2400m; 喜马拉雅山次之, 冰川分布在 4351~6600m, 高程跨度达 2200m; 冈底斯山冰川分布在 5400~6200m, 高程跨度最小, 仅为 800m。

3.3 末次冰川作用区坡度与海拔的关系

从整体上看, 喜马拉雅山的坡度略大于纳木那尼峰和冈底斯山, 3 个区域末次冰川作用区坡度随海拔变化趋势一致(图 4)。海拔低于 4500m 时, 随着海拔上升, 喜马拉雅山和纳木那尼峰末次冰川作用区的坡度在波动中略为增加; 海拔在 4500~4600m 之间时, 3 个区域末次冰川作用区的坡度均陡降, 随后开始增加; 海拔在 5200~5300m 之间时, 增加趋势减缓, 在海拔 5300m 左右转为下降。

对 3 个区域末次冰川作用区坡度的分段统计结果(图 5)显示, 海拔低于 LGM 古冰川 ELA 的地区坡度最小, 集中分布在 10°以内, 峰值出现在 5°左右; 海拔高于现代冰川 ELA 的地区坡度最大, 且分布不集中。当海拔在 LGM 古冰川 ELA 与现代冰川 ELA之间时, 3 个区域的坡度分布规律不同, 纳木那尼峰坡度峰值为 10°左右, 喜马拉雅山和冈底斯山的坡度峰值为 15°左右。

4 讨论

4.1 研究区末次冰川作用区坡度变化规律

稳态造山带地形的坡度一般随海拔上升而增大, 但本文研究的 3 个区域中, 至少出现两次坡度由升转降的现象(图4)。

第一个转折点出现在海拔 4500m 左右(即LGM古冰川末端的海拔高度), 4500~4700m 之间坡度陡降。4500m 以下, 地形不受冰川作用的侵蚀, 外营力主要为流水作用。此转折点坡度变化巨大, 如喜马拉雅山和纳木那尼峰, 海拔升高仅 200m, 坡度降幅就高达 10°, 说明冰川作用显著地降低由流水作用侵蚀造成的坡度, 冰川对地形有夷平作用。此转折点之后, 坡度继续随海拔的上升而增大。

第二个转折点出现在海拔 5300m 左右(喜马拉雅山、冈底斯山和纳木那尼峰分别为5200, 5350 和5400m), 与 3 个区域 LGM 古冰川 ELA (喜马拉雅山、冈底斯山和纳木那尼峰分别为 5350, 5400 和5486m)十分接近。海拔 5300m 以上, 坡度下降幅度很小, 均不超过 5°。对阿尔卑斯山的研究也发现类似的规律, 即坡度由上升转为下降的转折点位于LGM 古冰川 ELA 位置[19]。上述现象与冰锯理论中冰川切割作用最强烈的锯平带位于冰期与间冰期冰川平衡线之间的规律[3]十分吻合。此转折点反映LGM 古冰川 ELA 附近冰川切割作用最强。从图 4发现, 喜马拉雅山、冈底斯山和纳木那尼峰的锯平带分别为 5200~5450m, 5250~5500m 和 5300~5550 m, 位于 LGM 古冰川平衡线附近, 并非 Egholm 等[3]认为的 LGM 古冰川 ELA 与现代冰川 ELA 之间。

图 4 显示, 坡度最小的并不是中间的锯平带, 而是海拔低于古冰川 ELA 的地带。坡度虽在 LGM古冰川 ELA 附近出现转折, 但降幅很小, 冰川切割作用只抑制坡度增加的趋势, 古冰川作用区内坡度整体上依然随海拔上升而增加, 即使冰期与间冰期ELA 之间冰川切割作用最强, 海拔低于 LGM 古冰川 ELA 地区的坡度依然小于中间地带。

4.2 地形的海拔分布规律与构造抬升作用

Pedersen 等[15]研究全球冰川作用区的海拔分布, 发现地表绝大部分冰川作用区位于现代雪线以下, 低于现代雪线的某个海拔高度是地表冰川作用最集中的区域。以该海拔高度为基准(不同地区的基准海拔不同), 冰川作用区面积占比随海拔升高呈指数级衰减; 在现代雪线与 LGM 雪线之间, 面积占比随海拔降低呈线性衰减。青藏高原冰川作用区在现代雪线以上的面积占比仅为 10%, 在现代雪线以上 500m 的区域仅为 1%[15]。

从图 3 可以看出, 喜马拉雅山、冈底斯山和纳木那尼峰现代冰川 ELA 以上海拔高度的比例分别为 10.23%, 7.32%和 13.64%, 地表冰川作用区面积随高度呈指数级衰减的规律十分明显, 与 Pedersen 等[15]的研究结果相符。

图 3 显示, 喜马拉雅山冰川作用有 4800~5000 m 和 5200~5600m 两个集中分布区间, 推测 4800~ 5000m 的区间是高原面地势平坦, 海拔集中分布在4800~5000m 所致, 而 5200~5600m 区间略低于锯平带区间(5350~5700m), 但两者基本上吻合; 冈底斯山冰川作用最集中的区间为 5500~5700m, 落在锯平带区间(5400~5817 m)内; 纳木那尼峰冰川作用海拔分布最集中的区间为 5500~5900m, 同样落在锯平带区间(5486~5955m)内。上述结果说明喜马拉雅、冈底斯山和纳木那尼峰冰锯作用显著, 使末次冰川作用区海拔分布趋于向现代冰川 ELA 集中。上述海拔分布规律与全球冰川作用区大致吻合, 反映冰川对山地地形的侵蚀作用, 且锯平带上的侵蚀作用最强烈, 使得大部分冰川的高度落在锯平带区间, 冰川作用区在冰川 ELA 以上的分布受限。

Pedersen 等[15]还发现, 冰川作用区在雪线以上的海拔分布与山体隆升速率以及最近一次造山运动发生的时间有关。在构造活跃的地区, 峰顶至雪线的高程差与山脉的最高海拔保持一致, 随山体隆升速率的增加而增大。在构造不活跃的地区, 峰顶至雪线的高程差极小, 最高海拔也接近雪线。喜马拉雅山、冈底斯山和纳木那尼峰在现代冰川 ELA 以上的峰顶至雪线的高程差分别为 1100, 800 和 1700 m, 其中纳木那尼峰的抬升速率最快, 故高程差最大, 与 Pedersen 等[15]的研究结果相符。虽然冰川对地表有强烈的侵蚀作用, 但冰斗后壁的高度依然很大, 山脉的高度不完全由冰川侵蚀作用决定。纳木那尼峰因强烈的抬升作用, 最高海拔比冈底斯山高1000m。冈底斯山的现代海拔与 24MaBP 时无明显的差异[44], 故峰顶至雪线的高程差仅为800 m。

总之, 构造抬升作用加剧冰川作用对地形的侵蚀, 降低冰川区的坡度, 但冰斗后壁的坡度反而增加, 并且山脉高度不会完全受限, 依然继续抬升。

4.3 冰锯作用与气候的关系

气候是冰锯作用的主要影响因素[13], 控制青藏高原气候变化的决定性因素是西风以及印度季风两大环流[45]。西风与印度季风具有反相位变化的关系[46]: 夏季西风带北移, 西风急流减弱, 同时印度季风北移且增强, 带来的降水增多; 冬季西风带南移, 青藏高原上空的天气系统为中纬度季风, 冬季降水主要来自西风带。在距今 2.4~1.65 万年前的冰盛期与冰消期, 青藏高原主要受横跨欧亚大陆的西风控制, 之后主要受印度季风影响[42]。由于冰期与间冰期的温差可达 6~7℃[47], 可以类比冬季与夏季, 因此冰期内西风急流加强, 位置南移。Schiemann等[48]研究 80°—90°E 范围内 40 余年的西风带与西风急流数据, 发现西风急流的位置与风速、气温及降水量有关。在本文研究区域, 当西风急流偏南时, 月均降水量增多, 气温降低, 风速增强, 为冰川发育创造良好的条件。因此, 在冰期, 本文研究区内冰川发育程度增强, 冰锯作用也得到增强。

5 结论

本文通过计算青藏高原西南部喜马拉雅山、纳木那尼峰和冈底斯山 3 个地区现代冰川与 LGM 古冰川 ELA 以及地表高程频谱, 分析冰川作用区坡度与海拔的关系, 得出以下结论。

1)冰川对地形的剥蚀作用明显, 显著降低坡度。冰锯作用最强烈且对坡度降低最明显的地带位于LGM古冰川平衡线附近。

2)90%左右的冰川作用区位于现代冰川 ELA 以下, 分布最集中的区域位于锯平带, 表明冰锯作用对地形有显著的夷平作用, 使得地表海拔集中分布在现代冰川平衡线之下。

3)不同地质构造背景的山地, 冰锯作用的表现有所差异。强烈的构造抬升会加剧冰川对地表的夷平作用, 但非冰川区和冰斗后壁的坡度反而增加。同时, 构造抬升区的山脉高度只在一定程度上受限于冰锯作用, 但抬升量不会被冰锯作用完全抵消。

4)冰期时, 研究区冰川作用的加强由西风急流南移驱动, 为冰川发育提供较为有利的水热条件, 因此冰川发育程度增强, 冰锯作用也得到增强。

[1] Small E E, Anderson R S. Geomorphically driven late Cenozoic rock uplift in the Sierra Nevada, California. Science, 1995, 270: 277‒281

[2] Brocklehurst S H, Whipple K X. Glacial erosion and relief production in the Eastern Sierra Nevada, Cali-fornia. Geomorphology, 2002, 42(1/2): 1‒24

[3] Egholm D L, Nielsen S B, Pedersen V K, et al. Glacial effects limiting mountain height. Nature, 2009, 460: 884‒887

[4] Cuffey K M, Paterson W S B. The Physics of Gla-ciers. 4th ed. Oxford: Pergamon, 2010

[5] Harbor J M, Hallet B, Raymond C F. A numerical model of landform development by glacial erosion. Nature, 1988, 333: 347‒349

[6] MacGregor K R, Anderson R S, Anderson S P, et al. Numerical simulations of glacial-valley longitudinal profile evolution. Geology, 2000, 28(11): 1031‒1034

[7] Boulton G S. Theory of glacial erosion, transport and deposition as a consequence of subglacial sediment deformation. Journal of Glaciology, 1996, 42: 43‒62

[8] 刘俊男, 刘耕年, 彭旭, 等. 喜马拉雅山亚东‒康马段现代冰川平衡线高度、分布特征及影响因素. 北京大学学报(自然科学版), 2018, 54(2): 398‒406

[9] Ohmura A, Kasser P, Funk M. Climate at the equi-librium line of glaciers. Journal of Glaciology, 1992, 38: 397‒411

[10] Oskin M, Burbank D W. Alpine landscape evolution dominated by cirque retreat. Geology, 2005, 33(12): 933‒936

[11] Mitchell S G, Montgomery D R. Influence of a glacial buzzsaw on the height and morphology of the Cas-cade Range in central Washington State, USA. Qua-ternary Research, 2006, 65(1): 96‒107

[12] Whipple K X, Kirby E, Brocklehurst S H. Geomor-phic limits to climate-induced increases in topogra-phic relief. Nature, 1999, 401: 39‒43

[13] Brozović N, Burbank D W, Meigs A J. Climatic limits on landscape development in the northwestern Him-alaya. Science, 1997, 276: 571‒574

[14] Foster D, Brocklehurst S H, Gawthorpe R L. Small valley glaciers and the effectiveness of the glacial buzzsaw in the northern Basin and Range, USA. Geomorphology, 2008, 102(3/4): 624‒639

[15] Pedersen V K, Egholm D L, Nielsen S B. Alpine glacial topography and the rate of rock column uplift: a global perspective. Geomorphology, 2010, 122(1/2): 129‒139

[16] Spotila J A, Buscher J T, Meigs A J, et al. Long-term glacial erosion of active mountain belts: example of the Chugach-St. Elias Range, Alaska. Geology, 2004, 32(6): 501‒504

[17] Ward D J, Anderson R S, Haeussler P J. Scaling the Teflon peaks: rock type and the generation of extreme relief in the glaciated western Alaska Range. Journal of Geophysical Research: Earth Surface, 2012, 117 (F1): 1‒20

[18] Thomson S N, Brandon M T, Tomkin J H, et al. Glaciation as a destructive and constructive control on mountain building. Nature, 2010, 467: 313‒317

[19] Robl J, Prasicek G, Hergarten S, et al. Alpine topo-graphy in the light of tectonic uplift and glaciation. Global and Planetary Change, 2015, 127: 34‒49

[20] Banerjee A, Wani B A. Exponentially decreasing erosion rates protect the high-elevation crests of the Himalaya. Earth and Planetary Science Letters, 2018, 497: 22‒28

[21] 戚学祥, 许志琴, 史仁灯, 等. 高喜马拉雅普兰地区东西向韧性拆离作用及其构造意义. 中国地质, 2006, 33(2): 291‒298

[22] 姚檀栋, 蒲健辰, 田立德, 等. 喜马拉雅山脉西段纳木那尼冰川正在强烈萎缩. 冰川冻土, 2007, 29 (4): 503‒508

[23] 杨建强, 易朝路, Owen L A, 等. 藏西南纳木那尼峰地区第四纪以来的冰川演化. 第四纪研究, 2006, 26(2): 211‒219

[24] Owen L A, Yi C, Finkel R C, et al. Quaternary glaciation of Gurla Mandhata (Naimon’anyi). Quater-nary Science Reviews, 2010, 29(15/16): 1817‒1830

[25] Chevalier M L, Ryerson F J, Tapponnier P, et al. Slip-rate measurements on the Karakorum fault may imply secular variations in fault motion. science, 2005, 307: 411‒414

[26] Chevalier M L, Hilley G, Tapponnier P, et al. Con-straints on the late Quaternary glaciations in Tibet from cosmogenic exposure ages of moraine surfaces. Quaternary Science Reviews, 2011, 30(5/6): 528‒554

[27] Yin A, Harrison T M. Geologic evolution of the Himalayan-Tibetan orogen. Annual Review of Earth and Planetary Sciences, 2000, 28: 211‒280

[28] 朱大岗, 孟宪刚, 邵兆刚, 等. 西藏阿伊拉日居山南麓第四纪冰川沉积物及其ESR年龄测定. 冰川冻土, 2005, 27(2): 194‒198

[29] 朱大岗, 孟宪刚, 邵兆刚, 等. 西藏札达盆地及周缘高山区第四纪冰川堆积及冰川进退规程讨论. 中国地质, 2006, 33(1): 86‒97

[30] 张青松, 王富葆, 计宏祥, 等. 西藏札达盆地的上新世地层. 地层学杂志, 1981, 5(3): 216‒220

[31] 孟宪刚, 邵兆刚, 韩建恩, 等. 青藏高原古近纪‒新近纪重点古湖泊环境演变序列. 北京: 地质出版社, 2011

[32] Tapponnier P, Peltzer G, Armijo R. On the mechanics of the collision between India and Asia. Geological Society, London, Special Publications, 1986, 19(1): 113‒157

[33] 李海兵, Valli F, 刘敦一, 等. 喀喇昆仑断裂的形成时代: 锆石 SHRIMPU-Pb 年龄的制约. 科学通报, 2007, 52(4): 438‒447

[34] 王世锋, 江万, 王超. 喀喇昆仑断裂沿雅鲁藏布江缝合带活动的构造地貌特征. 地球科学与环境学报, 2016, 38(4): 483‒493

[35] 尹安. 喜马拉雅造山带新生代构造演化: 沿走向变化的构造几何形态、剥露历史和前陆沉积的约束. 地学前缘, 2006, 13(5):416‒515

[36] 刘焰, Siebel W, 王猛. 东喜马拉雅构造结陆内变形过程的研究. 地质学报. 2006, 80(9): 1274‒1284

[37] 许志琴, 杨经绥, 李海兵, 等. 印度‒亚洲碰撞大地构. 地质学报, 2011, 85(1): 1‒3

[38] 刘时银, 郭万钦, 许君利. 中国第二次冰川编目数据集(V1.0)(2006—2011). 北京: 国家青藏高原科学数据中心, 2012, doi: 10.3972/glacier.001.2013.db

[39] Hergarten S, Wagner T, Stüwe K. Age and prematurity of the Alps derived from topography. Earth and Pla-netary Science Letters, 2010, 297(3/4): 453‒460

[40] Robl J, Prasicek G, Hergarten S, et al. Alpine topo-graphy in the light of tectonic uplift and glaciation. Global and Planetary Change, 2015, 127: 34‒49

[41] Benn D I, Owen L A, Osmaston H A, et al. Recon-struction of equilibrium-line altitudes for tropical and sub-tropical glaciers. Quaternary International, 2005, 138: 8‒21

[42] Lichtenecker N. Die gegenwärtige und die eiszeitliche Schneegrenze in den Ostalpen // Gӧtzinger G. Ver-handlungen der III Internationalen Quartär-Conferenz. Vienna, 1936: 141‒147

[43] Manley G. The late-glacial climate of North-west Eng-land. Liverpool and Manchester Geological Journal, 1959, 2(2): 188‒215

[44] 许强, 丁林. 冈底斯山的隆升过程与青藏高原古高度研究. 中国科学基金, 2015, 29(1): 54‒59

[45] 姚檀栋, 朴世龙, 沈妙根, 等. 印度季风与西风相互作用在现代青藏高原产生连锁式环境效应. 中国科学院院刊, 2017, 32(9): 976‒984

[46] Benn D I, Owen L A. The role of the Indian summer monsoon and the mid-latitude westerlies in Himalayan glaciation: review and speculative discussion. Journal of the Geological Society, 1998, 155(2): 353‒363

[47] 姚檀栋, 刘晓东, 王宁练. 青藏高原地区的气候变化幅度问题. 科学通报, 2000, 45(1): 98‒106

[48] Schiemann R, Lüthi D, Schär C. Seasonality and interannual variability of the westerly jet in the Tibe-tan Plateau region. Journal of Climate, 2009, 22(11): 2940‒2957

Effect of Glacial Buzzsaw during Quaternary in Puland, Tibet

GUO Hao, LIU Gengnian†

College of Urban and Environmental Sciences, Peking University, Beijing 100871; † Corresponding author, E-mail: liugn@pku.edu.cn

In order to verify the effect of glacial buzzsaw on the evolution of landform in Pulan region of Tibet, three areas of Gurla Mandhata (Naimon’anyi), Himalayas and Gangdese are selected. Based on digital elevation model (DEM) data, remote sensing images, the equilibrium line altitude (ELA) of modern glacier and last glacial maximum (LGM) glacier, the relationship between slope and elevation and the elevation distribution are calculated and analyzed. We conclude that the areas with significant glacier erosion and the most obvious slope reduction are located in the area near LGM glacial equilibrium line and the heights of the mountains are limited in some degree. Based on the glacial landform characteristics and previous investigations, we believe that climate is the most important factor influencing the effectiveness of glacial buzzsaw. During glacial periods, the westerly jets moved southward, wind speed and precipitation increased, and the precipitation increased, resulting in favorable conditions for the development of glaciers and the effect of glacial buzzsaw. For mountains with strong tectonic uplift, such as Gurla Mandhata in the study area, although the effect of glacial buzzsaw is strengthened, the height increase caused by tectonic uplift is not completely offset by glacial buzzsaw.

glacial buzzsaw; equilibrium line altitude (ELA); elevation; slope; tectonic uplift; climate

10.13209/j.0479-8023.2020.075

国家自然科学基金(41771005)资助

2019‒10‒10;

2020‒06‒24