用不同的数学方法解决同一个物理问题

圣宝建

摘 要：数学在物理学中的应用是非常广泛的，使得物理需要依附数学而得以发展。有时候，人们可以借助数学方法来将一些较为复杂的物理问题转化为较为简单的数学问题。笔者介绍了利用数学里的导数思想求一元函数的最值和三元平均值不等式求最值的方法定理，并利用这两种不同的数学方法巧妙地解决了物理学静电场中的“等量的两个同种正电荷连线中垂线上最大电场强度”的问题。

关键词：数学;最大电场强度;导数;三元平均值不等式

中图分类号：G712 文献标识码：A

Abstract：The extensive application of modern mathematics in physics makes physics develop depending on mathematics.Sometimes，people can use mathematical methods to transform some more complex physical problems into simpler mathematical problems.In this paper，the author introduces how to use the idea of derivative to find the inequality of the maximum value and the mean value inequality of three variables in mathematics，and how to use these two different methods to ingeniously transform the "maximum electric field intensity problem on the vertical line of two equal positive charge lines" in physics electrostatic field into the problem of finding the maximum value of the function in mathematics.

Key words：mathematics;maximum electric intensity;derivative;mean value inequality of three variables in mathematics

伟大的数学家拉格朗日曾经说过，他不用画一张图，就可以用数学分析的方法来解决力学中所有的问题。由此可见，这两门学科之间关系密切。笔者利用导数和三元平均值不等式这两种不同的方法巧妙地将物理学静电场中“等量的两个同种电荷连线中垂线上最大电场强度的问题”转化为数学里求一元连续函数在开区间内的最大值问题，并得到了相同的结果。

1 问题的提出

物理学中的电场强度是一个既有大小又有方向的矢量，单个的点电荷在真空中的电场的计算，直接套用电场强度的决定式[1]公式即可，而在空间中同时存在多个（本文只讨论两个）点电荷，这时在空间某点产生的电场强度便是两个点电荷共同作用的结果，考虑到电场强度的矢量性，我们可以用数学里矢量的叠加法则—平行四边形法则来解决，所以，P点的电场强度应该等于两个点电荷各自在P点产生的电场强度的矢量和。为了描述方便，本文只介绍电荷量相等的两个正电荷（负电荷类似）共同作用在P点时的电场强度的最大值问题[2]的两种不同的数学求解方法。

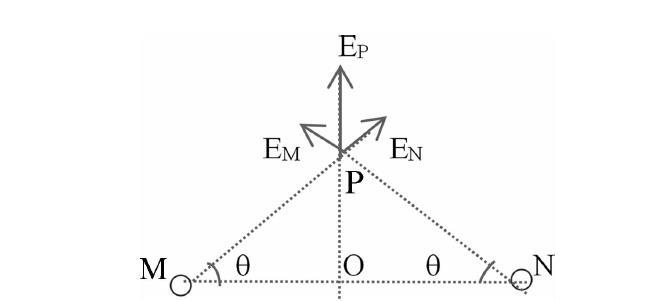
假设点P位于两个带有等量的同种正电荷的点电荷M、N连线的垂直平分线上（如下图），如下图所示，求M和N在P点处共同产生的最大电场强度（可以简称场强）。

我們知道，正电荷M和N各自在它们连线的中点O处会产生大小相等但方向相反的电场强度，所以，当P点恰好位于O点时，此时M和N在P点处产生的电场强度为零，是个定值，没必要讨论。下面我们探讨P点不在O点时的情况。由于同种电性的电荷相互排斥，所以O点处附近的电场线非常稀疏，但电场强度并不为零，考虑到在等量的同种正电荷M和N的连线的垂直平分线上，从O点到无穷远处，电场线是先变得密集后变得稀疏，那么电场强度是先变强再变弱的，从而，电场强度的最大值是客观存在的，笔者在下文中给出了两种不同的数学求解方法。

2 预备知识

2.1 真空中的点电荷形成的场强E的计算公式[3]

2.2 极值的判定定理[4]

2.3 最值的判定定理[4]

2.4 三元平均值不等式[5][6]

3 问题的两种数学解决方法

由物理对称性可知，在两个电性相同、电量相等的点电荷的连线的中点处的电场强度为零，且P点的合场强是沿着中垂线远离场源电荷且方向是竖直向上和竖直向下的，因为上下对称，所以竖直向上的合场强和竖直向下的合场强是等大的，故只需考虑竖直向上的情况即可。而由预备知识可知，在中垂线上距离O点无穷远处的电场强度大小也为零，所以，由公式（1）及矢量合成的平行四边形法则可知，从O点起，P沿着中垂线逐渐远离O点的过程中，P点处的合场强是先增大后减小，方向沿中垂线背离O点。所以，P点的合场强EP有最大值。下面我们给出两种不同的数学解决方法。

4 结语

由上面解决问题的过程，我们发现，数学和物理是相互渗透的，物理问题里渗透着数学思想和数学方法，数学思想和方法在物理中有独到的应用，这两大学科之间的关系真的非常密切，在好多方面都是相辅相成的。我们在解决一些物理问题时，如果能做到抓住问题的本质、处理得当，是可以把比较复杂甚至无法下手的物理问题轻松地转化为比较熟悉的数学问题的，是可以降低解决问题的难度的。文中，笔者在探讨等量的同种正电荷连线的垂直平分线上的点P处的电场强度的最大值问题时，就是运用物理概念和公式把问题的本质剖析出来，建立电场强度这样一个以距离为自变量的连续函数的数学模型，进而转化为求电场强度连续函数在开区间内的最值问题，然后分别借助于一元函数微积分学里的导数和不等式中的三元均值不等式巧妙地解决了文中提出的物理问题，所得结果也是一致的。

参考文献：

[1]课程教材研究所物理课程教材研究开发中心.物理选修3-1[M].第三版.北京：人民教育出版社，2014：1-14.

[2]沈克琦.高中物理学（3）电磁学[M].合肥：中国科学技术大学出版社，2015：6-13.

[3]温应春.高中物理一点一题型[M].合肥：中国科学技术大学出版社，2018：214-215.

[4]同济大学应用数学系.高等数学（下）[M].第五版.北京：高等教育出版社，2002：152-160.

[5]李胜宏，边红平.平均值不等式与柯西不等式[M].第三版.上海：华东师范大学出版社，2020：1-3.

[6]单墫.代数不等式的证明[M].合肥：中国科学技术大学出版社，2017：12.