钦州市需水量预测模型研究

樊洲洋，曾彦欣

(广西大学土木建筑工程学院，广西 南宁 530004)

1 概述

随着2017年北部湾城市群正式设立，钦州市作为北部湾城市之一，其定位为建设“一带一路”有机衔接重要门户港、区域性产业合作新高地、现代化生态滨海城市。为实现钦州市发展定位目标，必然要求其向城镇化、工业化以及农业现代化发展。然而近年来，钦州市用水趋势快速增加，仅2017年全年用水量为15.68亿m3。在供需矛盾、水资源利用率低的的背景下，钦州市需制定更加合理的区域用水配置方案，而需水量预测则是水资源合理配置的前提[2-3]。只有严格遵守水资源管理制度和合理配置水资源，才能为钦州市未来水资源可持续发展之路提供保障。现阶段的需水预测研究方法很多，如用水定额法、数字模型推算法(趋势分析法，因果分析法、时间序列法)等，李颖和张利伟[4]在验证不同需水方法中讨论了模型的适用性，并进行验证与总结。董云程等[5]发现采用神经网络更适合短期预测需水量，且许多学者通过大量成熟的研究方法验证了神经网络的使用条件。如牟天蔚将深度学习应用于城市日需水量预测，提高了预测精度。由于发展程度存在差异，各个城市都会存在适合当地的需水预测方法。本论文通过模拟2006—2018年钦州市用水量情况，比较人工神经网络法、灰色预测模型以及定额法3种方法的需水量预测结果，分析各自方法的优缺点，为钦州市日后水平年需水量预测提供借鉴。

2 钦州市水资源概况

钦州市地处广西自治区南部，北部湾沿岸，位于北纬21°35′～22°41′，东经107°72′～109°51′，面积为10 897 km2，多年平均降雨量为1 760.1 mm，地表水资源丰富。截止2018年统计得，多年平均地表水资源量为103.5亿m3，而2018年当地总用水量仅为 15.59亿m3，水资源开发利用率为15.1%。

表1为2006—2017年钦州市农业灌溉用水、居民生活用水量、工业用水3个用水影响因子统计表。从表1中计算发现，钦州市70%左右的用水量都是在农业灌溉领域。

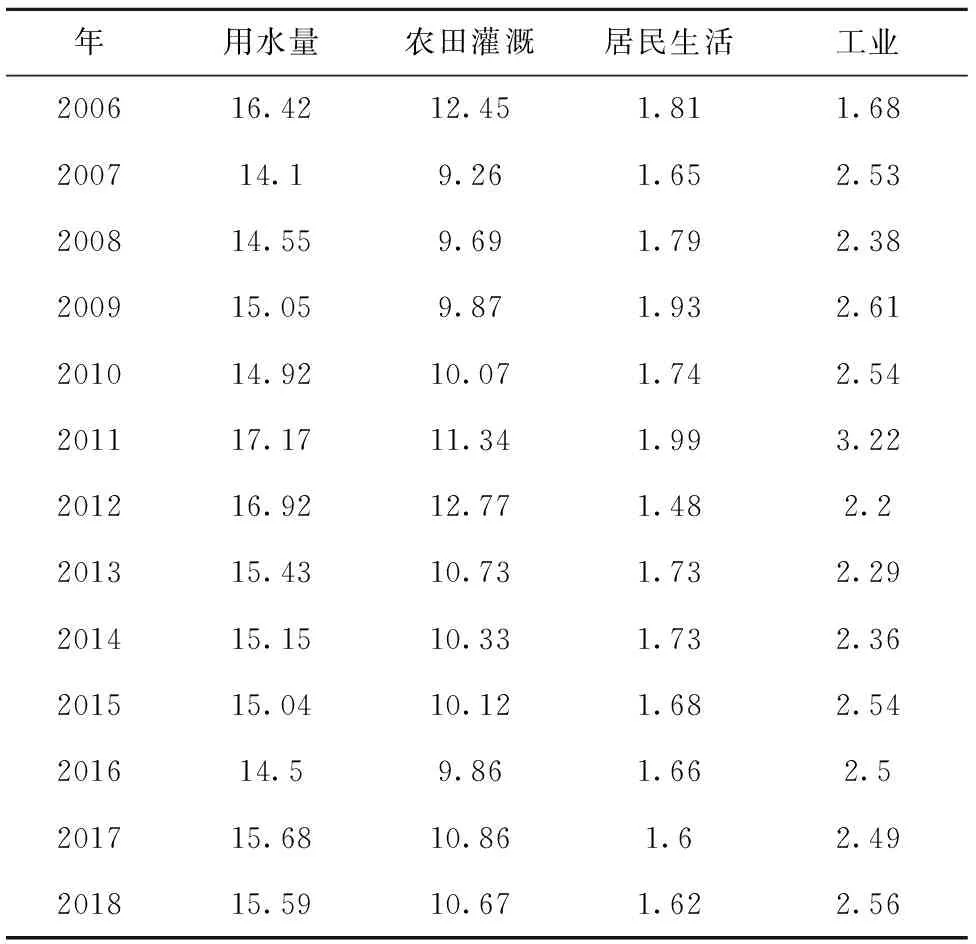
表1 2006—2017年钦州市用水量及影响因子统计 /亿m3

3 理论方法介绍

钦州市需水量预测重在讲究数据的真实、可靠、误差较小。本文所选方法各有其特点，有的需要大量的数据预测训练模型；有的模型只考虑单一需水量就可预测；还有的与时间长短有关，分别进行介绍。

3.1 人工神经网络模型

人工神经网络模型，具有自学习、非线性和自组织、大规模并行等优点，而本文中应用的BP神经网络模型在学习中具有双向传播的功能：既可以进行信号正向传播过程，同时，也具有误差的反向传播过程[7]，因此，本文选择BP神经网络作为研究方法之一。在正向传播与反向传播的权值调整中，也就是训练BP神经网络的过程，网络训练的目的就是要减小误差，直到需要的精度或者到设定的学习次数[8]为止。3层BP神经网络结构示意如图1所示。

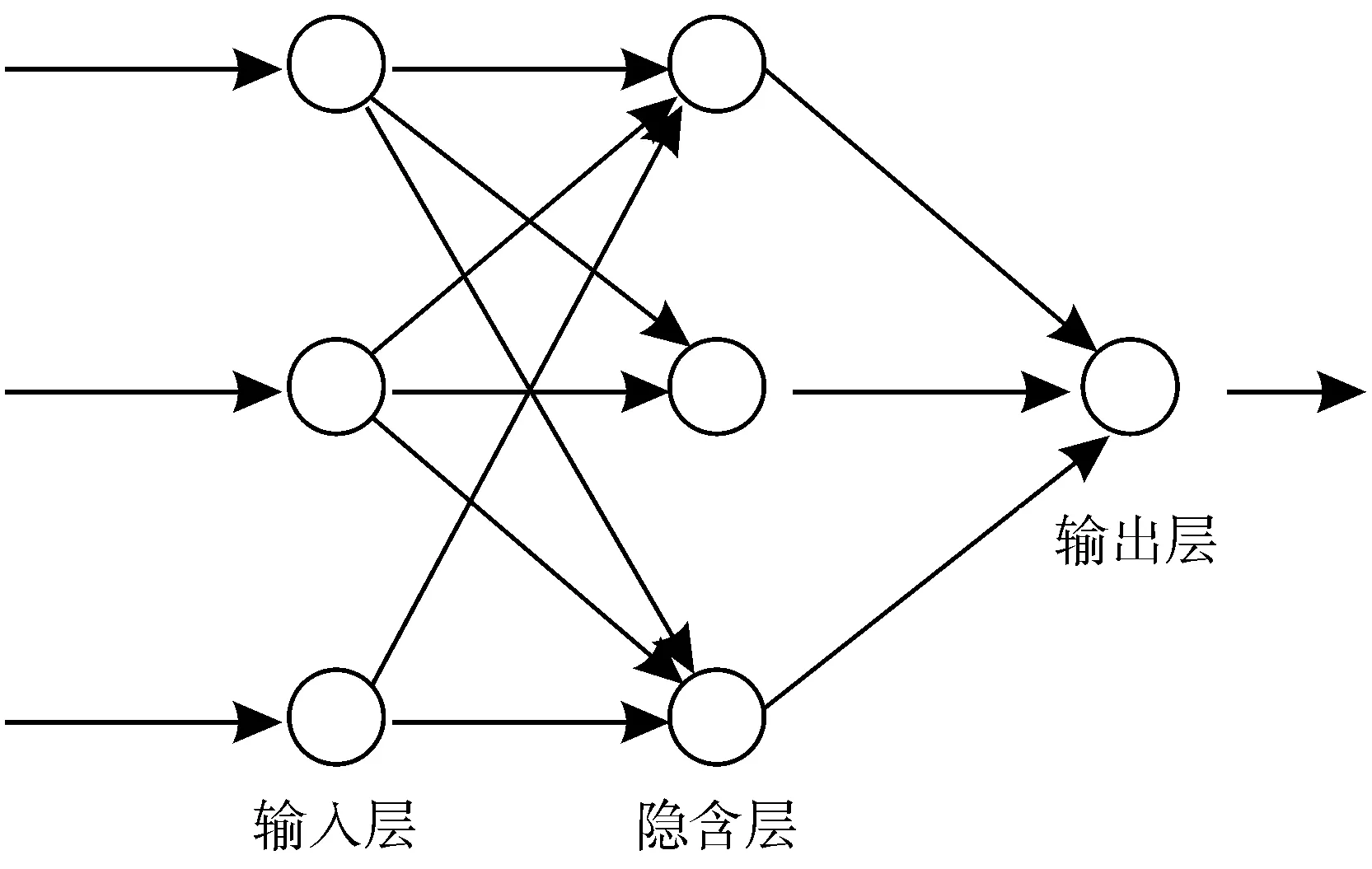
图1 BP神经网络结构示意

算法学习过程：① 将空间内随机的值赋予每个阈值φj、ξt和连接权限ωij、τjt；② 随机选择一组数据输入Xk=(x1，x2…xm)T，Zk=(δ1，δ2…δm)T提供给神经网络中；③ 计算神经网络隐含层的输入和输出，如式(1)(2)；④ 计算神经网络的输出层的输入输出，如式(3)(4)；⑤ 计算各层的误差，如式(5)(6)并修正阈值和连接权限值，公式如(7)(8)(9)(10)；⑥ 反复进行上述②～⑤的操作达到误差要求。

隐层神经元输入输出：

(1)

yi=f1(Sj)

(2)

输出层神经元输入输出：

(3)

Tit=f2(Ht)

(4)

一般化误差:

(5)

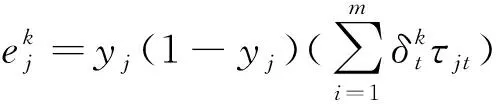
(6)

权重更新:

(8)

(10)

式(9)(10)中α、β为学习率，取值范围0～1。

3.2 灰色预测模型

灰色预测模型是一种数学模型，是以较少信息建立数学模型，然后预测的方法。需要的数据较少，样本分布不需要规律性、精度较高，因此，基于这3点选择灰色预测模型作为研究方法之一。将已知的、未知的信息分别视为白色、黑色系统，因此，该模型可视为既包含已知信息又有未知信息的灰色系统[4]。同时，该模型认为一定区域内需水量与时间等因子有关，可以预测城市日、月、年的需水预测。GM(1，1)模型[9]是单阶变量微分方程，也是单序列动态模型。将明显没有关系的时间序列，通过数学方法(累加生成累减生成加权累加生成)变得有关系是其基本思想。该方法需要的影响因子少，方便简单，通过对数据进行运算，使之呈现指数变化，预测未来发展趋势。该灰色模型微分方程为[10]：

(11)

(12)

(t取1，2，…，n)

还原数据得：

(13)

3.3 定额法

应用定额法，文中将用水预测目标分为生活用水、工业用水、农业用水、建筑业和第三产业用水以及生态用[11]。

3.3.1生活用水

生活用水包括城镇用水和农村用水。

3.3.2工业用水

工业需水包括一般工业和火电这两部分，所以需水量预测分为两部分：

(14)

式中W一般工业为某水平年一般工业需水量；Xi为某水平年工业产值(以万元计)；Ti为某水平年万元取水定额,m3/万元；n表示部门数。

(15)

式中W火电为某水平年火电所需水量；Pi为电机组容量,万kW；Qi为用水定额,m3/(万kW·h)。

3.3.3农业用水

农业用水包含农、林、牧、渔四部分用水，其中在农田灌溉运用定额法进行计算：

W农业=∑∑ωijvij/λij

(16)

式中W农业为某水平年农业需水量；ωij为某作物灌溉面积；vij为用水定额；λij为农田利用系数。

3.3.4建筑业和第三产业用水

该部分应用万元增值法进行预测，即用水量为建筑业或第三产业万元增值与用水定额的乘积。

3.3.5生态用水

生态用水在此主要指道路洒水和绿地、河湖等补水部分：

W生态需水=h城镇q生态

(17)

式中W生态需水为水平年生态需水量；q生态为道路洒水和绿地、河湖等补水部分的定额；h城镇为城镇人口数。

4 不同需水模型预测

4.1 人工神经网络模型

以农业灌溉用水、居民生活用水量、工业用水3个用水影响因子的数据为神经网络输入量，钦州市历年用水量为输出量，建立钦州市3层BP神经网络。在BP神经网络中，2006—2018年相关数据即为训练样本又为检验样本，将数据进行训练。首先原始数据进行归一化处理，在BP网络中输入数据进行学习训练；其次设定网络初始参数值，基本参数如下：迭代次数为50，学习率为0.05，最大训练次数为3 000，训练目标精度为0.001，训练函数为TRAINGDM，全局误差函数选为均方误差；最后经过学习训练得到最终模型训练结果(如表2)。

4.2 灰色预测模型

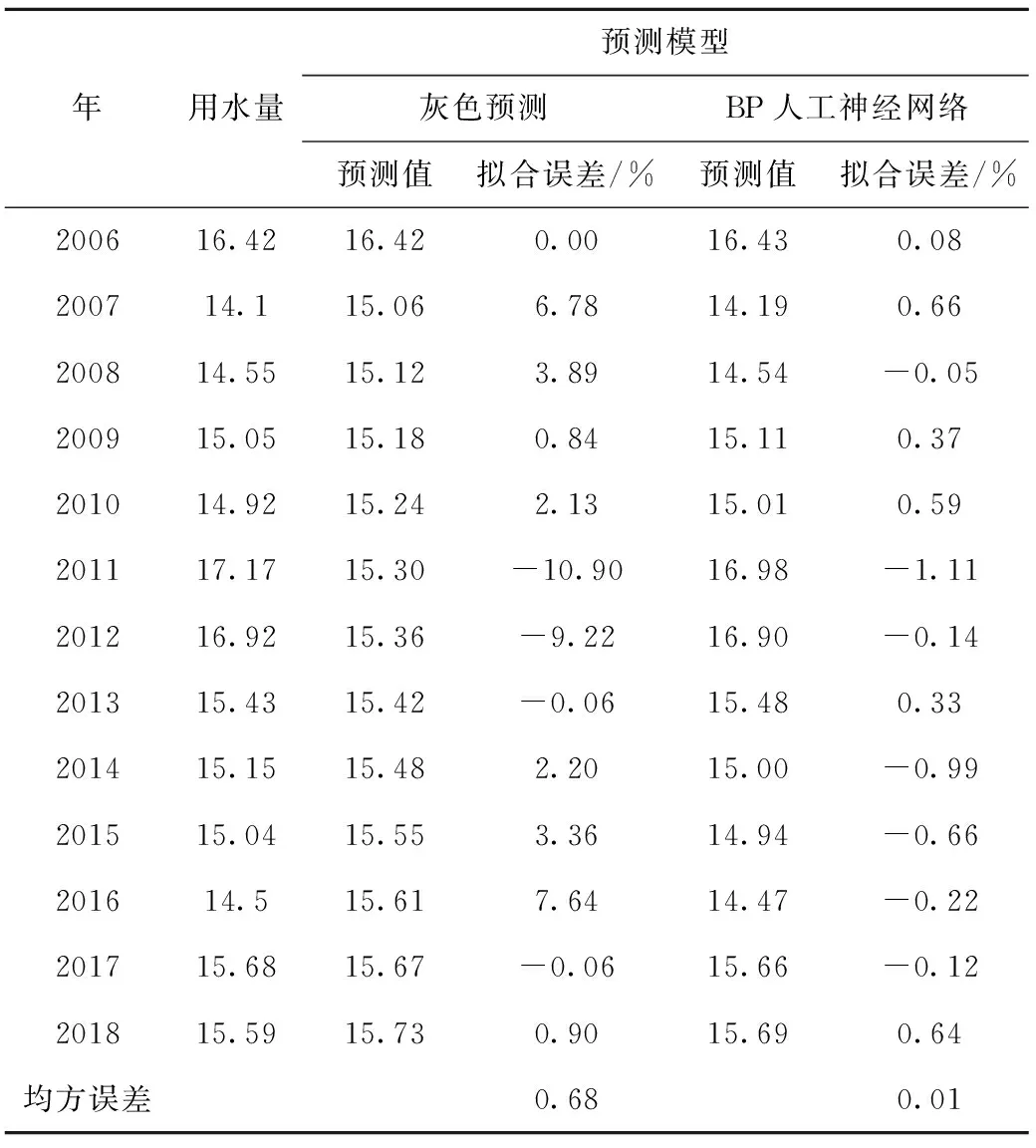
表2 不同预测模型下的钦州市需水预测值与真实值 亿m3

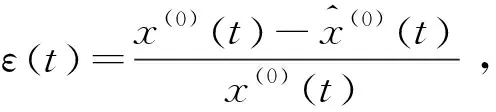
4.3 定额法

依照定额法，计算得P=75%的来水频率下2018年钦州市需水量(见表3)，并附上计算得2018年钦州市各部分的用水定额(见表4)，定额法计算误差为1%；均方误差为0.03。

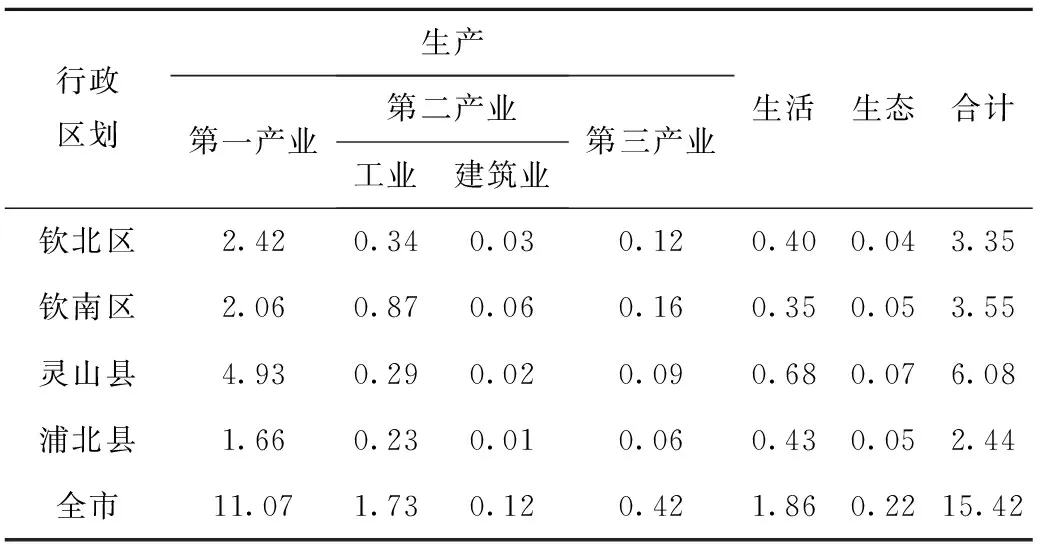
表3 定额法计算下的钦州市用水量 亿m3

表4 钦州市2018年用水计算定额

5 结果分析

表2灰色预测模型、BP神经网络、定额法3种模型的均方误差分别为：0.68、0.01、0.03，可以看出：BP神经网络模型结果最优、精度最高，定额法次之，灰色预测模型最后、精度较差。对比3种方法的拟合误差可以发现：除2013年、2017年灰色预测模型精度比BP神经网络较高外，灰色预测模型整体相对误差数值波动较大，而BP神经网络模型预测，除2011年、2014年拟合误差超过1%，其余年都是0.5%左右。

为验证3种模型拟合效果，以《钦州市“十三五”水资源行业配置方案》中2020年钦州市用水量进行验证。分别用上述3种方法计算得：灰色预测模型计算下的需水量为15.86亿m3，误差为4%，BP神经网络计算下需水量为16.59亿m3，误差为0.36%，定额法计算下需水量15.75亿m3，误差为4.7%。

经上述分析可得，3种方法中BP神经网络模型的精度最佳，结果得到了验证。因此，BP神经网络模型是模拟钦州市用水量的适用方法，且能比较明显的反映出来钦州市用水量变化情况。进一步通过2006—2018年数据，利用BP神经网络推算得2025年，钦州市用水量为16.6亿m3，未来几年内钦州市需水量仍将缓慢增长。

6 结语

本文利用3种模型预测钦州市需水量，分析结果得到以下认识和结论：① 采用BP神经网络模型模拟需水量时，该方法引用的钦州市相关数据既是训练数据也是验证数据，经过多次训练验证后所得结果误差较小，泛化和容错能力较好，精度较高，使得预测钦州市需水量时较准确。② GM(1，1)灰色预测模型预测效果较差，因为拟合是一条指数曲线，要求数据累加需要具有指数性质，当数据累加不具有其性质时，拟合效果比较差，由于钦州市用水量累加数据的指数性质较差，因此使用该模型预测钦州市需水量未达到预期效果。③ 定额法在计算钦州市需水量时，考虑方面比较多，必须需要大量、详细且全面的资料用来计算，结果才比较准确。

综上所述，BP神经算法在钦州市需水量预测中有较好的可行性，可为钦州市合理预测需水量提供思路。