基于多因素概率模型对玩家行为的研究
2020-11-30马晨昊宋舒娴李润含
马晨昊 宋舒娴 李润含
(1、大连海事大学信息科学技术学院,辽宁 大连116000 2、大连海事大学航海学院,辽宁 大连116000)
“穿越沙漠”游戏规定为:每名玩家在游戏开始时都会收到一定数额的资金与闯关地图,分别用来购买行进过程中必要的生活用品和规划全局路线,途中经过村庄可以用来补给资源,经过矿山并采矿能获得固定资金,玩家在探险途中还可能会遇到恶劣天气。在系统指定的时间内从起点处穿越沙漠到达终点即为通过,剩余的资金与资源越丰富获得优胜的机会越大。
1 问题分析
要在未知天气状况下建立模型制定玩家的通关策略。
首先我们对影响最终结果的所有可能进行分析得到玩家出发当天遇到高温天气做出的选择不确定性最大,为对游戏进行仿真模拟我们建立基于熵权法的TOPSIS 多因素概率模型得到高温天气下玩家倾向选择概率,并结合行走时间对其做出动态分析。
其次我们使用基于动态步长的逐天模拟算法结合两幅不同地图对所有最佳路线进行仿真,此算法特点主要有两点:一是对于天气状况的生成具有随机性;二是大量模拟结果使得每种情况最终值精确。
2 模型建立
基于熵权法的TOPSIS创新应用的多因素概率模型:
玩家在未知情况下遭遇高温天气时的选择会对最终结果产生很大影响。例如我们假设高温状态下玩家一律选择呆在原地休整,等到晴天时才往下一个目的地出发,这样造成的结果可能为未在规定时间内到达终点任务通关失败,或者是在矿山挖矿时间短收益小导致最终总体浪费资源过多;当假设玩家在高温状态下持续行走不做停留,造成的结果可能会是中途玩家拥有物资短缺不足以支撑到下一个目的地。为解决此类问题我们需对玩家在高温天气下选择停留的概率进行分析。
TOPSIS(优劣解距离法)为C.L.Hwang 与K.Yoon 在1981 年提出的一种综合评价方法,在已知原始数据信息的情况下评价结果能精确反应各评价方案之间的差距,是应用于多目标决策分析中的一种有效方法,具有过程简单,处理灵活方便等特点,适用于对玩家在不同情况下选取特定概率。
我们将玩家的每个选择视为对象,物资消耗与收获资金视为指标,已知各个指标对应的具体信息。对指标的权重赋值有很多方法如专家评判,但其主观性较强,不同评判会对结果产生很大影响,采用熵权法来尽可能利用数据信息对指标进行客观权重赋值。
下面我们利用基于熵权法的TOPSIS 模型对玩家面对不同情况选择概率进行具体求解。
3 模型求解
3.1 统一指标类型。资源消耗为极小型指标,消耗越多对选择越不利;争取资金为极大型指标,挣取越多对结果越有益。采用差值法对数据进行正向化处理,我们采用如下公式:maxi-Xi(1)

4 计算各选项与理想解的距离并归一化得到概率

其中S軌i∈[0,1],为归一化后的概率得分,通过求解我们得到玩家在第三关遭遇高温天气选择停留的概率为0.7672;在第四关遭遇高温天气选择停留的概率为0.5753。
5 时间-概率动态变化分析
前面已经利用TOPSIS 法对玩家在遭遇高温天气时选择停留进行客观评价并求解出具体概率数值,但真实情况往往更为复杂。在游戏开始后不久玩家遇到高温天气时会以一定概率选择是否继续行走,当游戏进程时间越靠近截止日期时玩家的心境会从理性变为焦急,在越接近游戏结束日期时会出于节省时间的考虑倾向于高温天继续行走这一选择。
指数函数通常适合用来描述两关联因素之间的规律变化特征,对其进行修改得到玩家在高温天气选择停留的概率与时间变化的关系,我们设:P=pie1-ti(i=1,2) (11)
其中i=1,2 分别代表第三关与第四关两种情况;P 为玩家在不同时间内遇到高温天气选择停留的概率;pi为关卡内游戏开始第一天为高温天气时玩家选择停留的概率,p1=0.7672,p2=0.5753;ti为从游戏开始到遇到高温的时间数,t1∈[1,10],t2∈[1,30]。
当i=1 即处于第三关时,假设玩家在第一天遇到高温,此时选择原地停留休整的概率最大,即为p1;当t1不断增大时选择概率不断缓慢下降最终趋于0,因此公式(9)能完整、合理地描述概率随时间动态变化过程。
6 结论
三个天气因素中高温的不确定性最大,因此玩家需要重点考虑高温天气下是否做出停留选择,当时间充裕时玩家出发当天为高温天以一定概率在原地休整,来减少资源消耗量(如果在矿山遇到高温天以更大的概率停留下来挖矿);当玩家所剩时间不多时,为保证自己能够按时到达终点,在除沙暴天外玩家尽可能赶路,最终到达终点。
根据生成的当局天气(晴天与高温)决定下一次的行动结果,特点为大量随机模拟利用Matlab 采用以上述步骤进行仿真,得到如图1-2 所示结果。
在5 种情况下的通关最大资金量对比图,分析图3-4 中信息我们得到:随着晴朗天数的增多,各情况在到达终点处的剩余资金呈单调上升趋势;晴天天数增加对循环两次的路线影响更加明显,对情况1 的影响最为薄弱;图中最大交叉点处位于第25 天,为情况1 与情况4 的交叉点;当晴朗天数几乎为0 时,除循环两圈的情况时终点剩余资金最少外,其余情况大多分布在6000 到8000 元之间。
接下来利用分析得到的信息对罗列出的所有情况进行筛选:在一定时间范围内随着晴朗天数的增加,循环一遍的剩余最大资金总是高于循环两遍的最大资金,合理推测循环三圈收获的效益会更低,因此我们排除循环多次的情况只考虑循环一圈的路线。
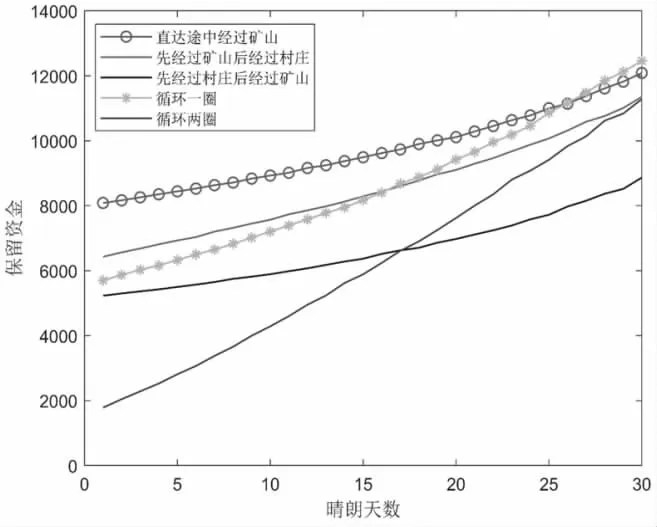
图1 五种情况下最大剩余资金量对比图
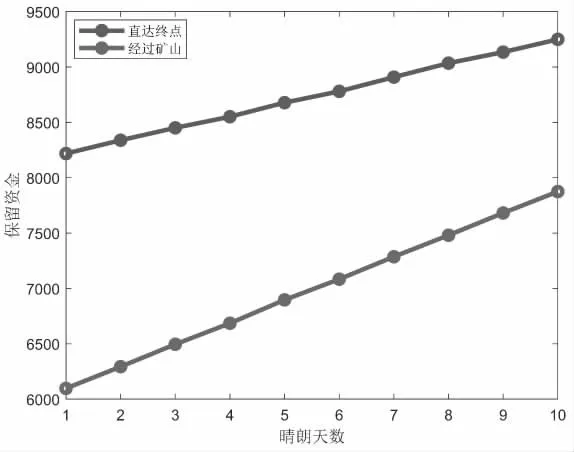
图2 所有天气状况下的最多剩余资金
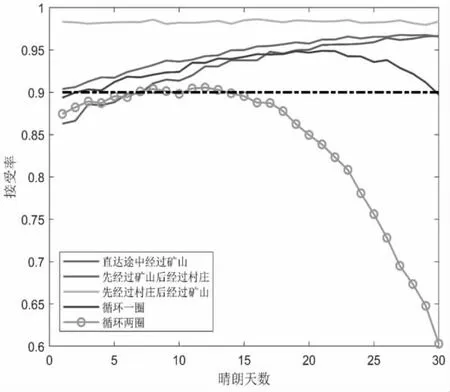
图3 稳定性评价
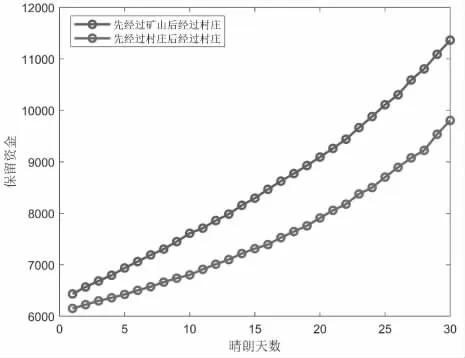
图4 先后经过村庄剩余资金量对比图
最后分析可知随着晴天天数的增加,先经过矿山后经过村庄获得的收益总是大于先经过村庄后经过矿山的收益。
