四足激光除草机器人腿部结构参数优化

张良安，唐 锴，赵永杰，王孝义，余大壮，卢新建，王 祥

·农业装备工程与机械化·

四足激光除草机器人腿部结构参数优化

张良安1，唐 锴1，赵永杰2※，王孝义1，余大壮1，卢新建3，王 祥1

（1. 安徽工业大学机械工程学院，马鞍山 243000；2. 汕头大学机械电子工程系，汕头 515063；3. 广东省智行机器人科技有限公司，佛山 528226）

电驱四足激光除草机器人的续航能力取决于其电池容量和自身功耗，为了提高其续航能力，降低其目标轨迹下的驱动力矩将具有重要意义。该文以四足激光除草机器人为研究对象，提出一种动力学尺度综合方法，将其腿部尺寸参数作为优化设计目的，在给定的目标轨迹上，针对腿部关节驱动力矩进行优化，最终得到一组最优腿部杆长，使其完成目标轨迹的驱动力矩和功耗最小。以四足机器人腿部关节驱动力矩最大值最小作为优化目标，腿部尺寸参数作为约束变量，利用粒子群算法和理想点法进行二次优化，将多目标优化问题转化为单目标优化问题，得到一组最优杆长。计算结果表明：经过尺度综合后的四足机器人动力学性能得到明显改善，优化后单腿的大腿关节驱动力矩峰值下降5.29%，小腿关节驱动力矩峰值下降18.05%，验证了该尺度综合方法的有效性。该文提出的动力学尺度综合方法可为四足类机器人的设计提供参考依据。

机器人；优化；尺度综合；粒子群算法

0 引 言

激光除草不使用农药，对保护生态环境具有重要意义。但激光器的运载平台不成熟是目前限制其推广使用的重要因素。国内外学者对怎样将机器人作为激光除草器的移动搭载平台进行了大量的研究[1-3]，而相对于目前的轮式和履带式机器人，四足机器人由于具有离散的落足点，能够灵活调整行走位姿和步态，因此更适合在其上搭载激光除草机构在农田等非结构环境中进行作业。

四足机器人的能源和动力不足问题一直是限制其进行应用发展的一大瓶颈。因此，研究四足机器人的移动能量消耗，分析影响其驱动力矩和功耗的因素，对于降低其功耗、拓宽其应用领域具有重要的意义。以往研究已经证实合理的结构参数和步态参数能够提高机器人的能量效率[4-6]。例如，马宗利等[7]针对四足机器人能耗进行分析，提出了一种大腿和小腿呈一体化的柔性节能结构，并对模型进行了动力学分析和ADAMS仿真，验证了该模型能够使得关节驱动力矩和功耗明显降低；雷静桃等[8]对四足机器人的足端轨迹进行了研究，分析了不同足端轨迹及步高、步距、关节起始角等步态参数对移动能耗的影响。李军等[9]针对不同步频与步幅的耦合状态，研究了步频与步幅的独立变化对四足机器人关节扭矩与功耗的影响，通过仿真验证得出能耗对步频参数的提升更为敏感。现有的四足机器人动力学和能耗研究中，较少涉及考虑整个机身质量分布在给定轨迹规划下，腿部结构参数对四足机器人动力学性能和功耗的影响。对四足机器人而言，合适的腿部参数可明显降低四足机器人的驱动力矩和功耗，提高机器人的动力学性能，拓展应用范围，因此，对四足机器人进行动力学尺度综合尤为重要[10-12]。

综上所述，为降低四足激光除草机器人的驱动力矩，本文提出一种基于目标轨迹下四足机器人动力学尺度综合优化设计方法。以Swil四足机器人为研究对象，建立其整机运动学和刚体动力学模型，并基于零冲击原则确定机器人足端运动轨迹。在目标轨迹下以腿部关节驱动力矩最大值最小化作为动力学性能优化目标，利用粒子群算法先对多目标函数进行优化，得到各关节驱动力矩峰值的最小值。最后根据理想点法将多目标问题转化为单目标问题进行二次优化，得到一组腿部尺寸参数，使得四足机器人的驱动力矩和功耗最小。

1 Swil四足机器人

所设计的Swil四足机器人主要由躯身和四条对称布置的腿部机构组成。具体结构如图1所示。

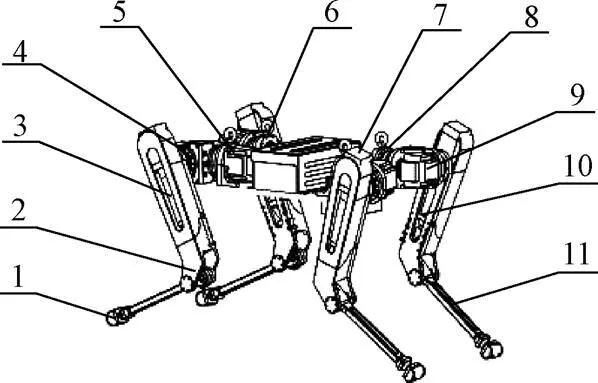
1.足端 2.曲柄连杆机构 3.大腿 4.髋关节减速器 5.侧摆关节电机 6.蓄电池 7.膝关节电机 8.侧摆关节减速器 9.髋关节电机 10.电动缸 11.小腿

在四足机器人结构设计上，Swil四足机器人的四条腿的大小尺寸相同，采用前肘后膝式的拓扑结构，对称布置在机身的四周，这有助于增强四足机器人的稳定性。四足机器人在直线运动时，髋关节处的电机驱动大腿使其绕着髋关节进行转动，实现其俯仰运动。小腿绕膝关节的转动是依靠将电动缸的直线运动通过曲柄滑块结构转化为小腿的转动，实现其腿部的抬落。通过大腿与小腿间的相互协调以及各腿部之间的连续步态，来实现四足机器人的运动。

2 运动学分析

四足机器人单腿D-H模型如图2所示，运用D-H法建立坐标系对四足机器人腿部结构关系进行描述。

注：b为机身半长，m；w为机身半宽，m；h为机身高度，m；zb为机身z轴坐标；yb为机身y轴坐标；xb为机身x轴坐标；Ob为机身坐标轴原点；x0为髋关节x轴坐标；y0为髋关节轴坐标；z0为髋关节轴坐标；θ1为侧摆关节转角，（º）；L1为髋部杆长，m；x1为髋部轴坐标；z1为髋部轴坐标；θ2为髋关节转角，（º）；L2为大腿杆长，m；x2为膝关节轴坐标；z2为膝关节轴坐标；θ3为膝关节转角，（º）；L3为小腿杆长，m；x3为足端轴坐标；z3为足端轴坐标。

根据四足机器人单腿结构简图，建立各关节处的空间坐标系，并通过各坐标系间的关系运用D-H法得到D-H连杆参数，如表1所示。

表1 D-H连杆参数表

注：表示关节转角，(°)；d表示关节距离，mm；a表示杆件长度，mm；表示杆件扭角，(°)；1表示髋部连杆，2表示大腿连杆，3表示小腿连杆。

Note:is joint angle, (°);dis linkage distance, mm ;ais linkage length, mm;is linkage twist, (°); 1 is the connecting rod of hip; 2 is the connecting rod of thigh; 3 is the connecting rod of shank.

四足机器人足端相对于侧摆关节在空间中的位置=(P,P,P)可由齐次变换矩阵表示为

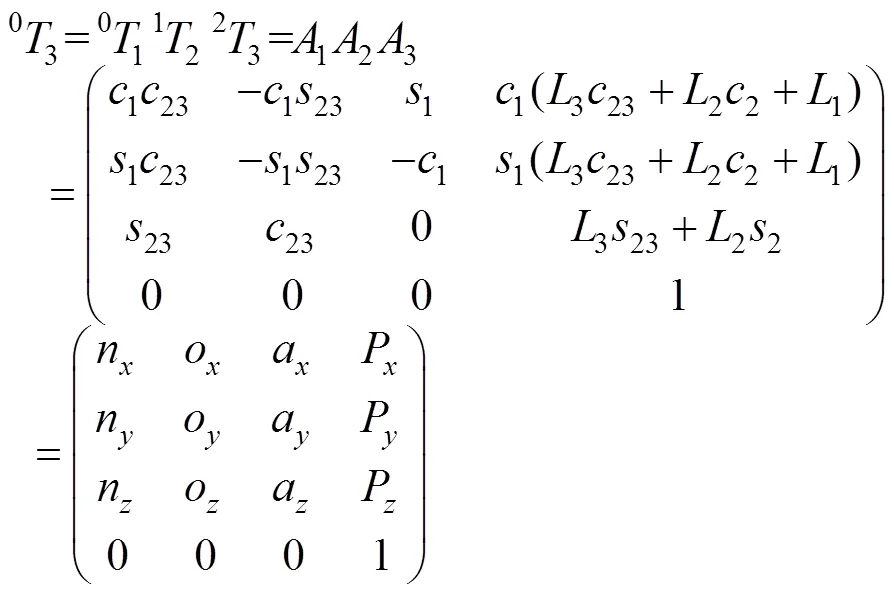
式中03表示足端坐标系相对于侧摆关节坐标系的位姿，01(称为1)表示髋关节坐标系相对于侧摆关节坐标系的位姿，12(称为2)表示膝关节坐标系相对于髋关节坐标系的位姿，23(称为3)表示足端关节坐标系相对于膝关节坐标系的位姿，P表示足端在侧摆关节坐标系下的轴坐标，P表示足端在侧摆关节坐标系下的轴坐标, P表示足端在侧摆关节坐标系下的轴坐标，=(n,n,n)表示足端轴的单位方向矢量，=(o,o,o)表示足端轴的单位方向矢量，=(a,a,a)表示足端轴的单位方向矢量，1=sin(1)，1=cos(1)，2=sin(2)，2=cos(2)，3=sin(3)，3=cos(3)，23=sin(2+3)，23=cos(2+3)

根据四足机器人D-H连杆参数表，可推导出其运动学正解为

为了对四足机器人进行轨迹规划和控制，我们需要对其进行逆运动学分析。依据公式（1）、（2），可分别求出各关节转动的角度，具体如下

其中，1=sin(1)，1=cos(1)，2=sin(2)，2=cos(2)，3=sin(3)，3=sin(1)，23=sin(1+3)，23=cos(2+3)

3 轨迹规划

本文是基于给定的目标轨迹下对四足机器人动力学性能进行研究，因此规划一条合理的能够满足任务需求的足端轨迹显得尤为重要[13-14]。据一些以往的研究发现在对四足机器人进行轨迹规划时，复合摆线轨迹能够减小足端与地面的冲击，且在运行稳定性方面也具有良好的效果[15-16]。考虑四足机器人关节速度、加速度连续性要求，结合预设的步态参数建立四足机器人足端约束方程，并推导出满足要求的复合摆线轨迹方程，再将得到的复合摆线轨迹与运动学方程相结合，来验证其轨迹规划的有效性。

3.1 足端轨迹

本文根据四足机器人完成任务要求，对其步态参数进行设置：步长=0.48 m，步高=0.08 m，单腿步态周期=2 s，单腿占空比=1/2，四足机器人摆动相与支撑相在0=1 s时进行切换。则在0～0，足端处于摆动相；在0～，足端处于支撑相[17-18]。设水平方向为方向，竖直方向为方向，为单腿运动时间，根据速度、加速度连续性要求建立足端轨迹方程：

方向上约束方程为

方向上约束方程为

支撑相函数为

则整个复合摆线的运动曲线如图3所示。

3.2 复合摆线轨迹的验证

为了验证所推导的复合摆线轨迹的正确性，首先建立基于复合摆线轨迹下的运动学模型简图，如图4所示。

注：m1为髋部杆质量，kg，m2为大腿质量，kg；m3为小腿质量，kg；H1为侧摆关节到地面的高度，m；A点为足端在复合摆线轨迹上的任意一点；h1为A点到地面的高度，m；B点为足端起始点，且在侧摆关节质心O点正下方。

以髋关节质心为原点，水平前进方向为轴，竖直方向为轴，建立坐标系。点在髋关节质心的正下方；点为足端在复合摆线轨迹上的任意一点。则可推导出基于复合摆线下的四足机器人单腿运动学数学表达式。

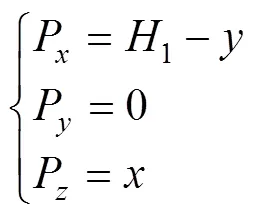
根据已知杆长（1,2,3）和式（8）以及表1，可推导出四足机器人逆运动学数学表达式为

为了对复合摆线轨迹进行验证，根据实验室原有的四足机器人结构尺寸，令1=0.64 m，1=0，2=0.42 m，3=0.36 m，并将3.1节中各步态参数代入式（9）中得到腿部关节的转角函数，并对其进行一阶和二阶求导分别得到角速度和角加速度函数。并在MATLAB中绘制出基于给定目标轨迹下的各关节运动曲线，如图5所示。

图5 各关节运动曲线

由图5可知，四足机器人在目标轨迹上速度、加速度连续，且在摆动相与支撑相切换的瞬间及0=1 s时足端加速度=0，减小了足端与地面的冲击，验证了复合摆线轨迹的可行性。

4 动力学分析

动力学模型可描述四足机器人的动态性能，反映各关节驱动力矩与运动参数间的关系，是四足机器人驱动力矩和移动功耗分析的基础。由于四足机器人在trot步态下，位于对角线上的两条腿同时处于支撑相或摆动相，所以四足机器人在运动过程中是变结构的，摆动相和支撑相时的运动学模型不同[19]。本文优化的目标是使四足机器人在目标轨迹上各关节驱动力矩峰值下降，而相对于摆动相时，支撑相的各关节驱动力矩要大的多，因此本文只对支撑相时的各关节驱动力矩进行分析。

当仅考虑到四足激光除草机器人的机身质量，而忽略其腿部质量时，假定四足机器人的所有质量都集中在机身的中心。由于四足激光除草机器人是一个复杂的多刚体系统，其足端与地面间的接触很难用模型来描述，因此本文将四足机器人简化为一个做平面运动的五杆机构，且在行走过程进行如下假设[20]

1）足端与地面间接触良好，且不存在相对滑动，则四足机器人与地面之间可以看作是铰链连接；

2）四足激光除草机器人以trot步态匀速运动时，地面对足端的支撑反力竖直向上，且只在竖直方向上有分量；

3）相对于四足机器人的机身质量，其腿部质量忽略不计，且假定所有质量都集中在机身的中心。

基于以上假说，对四足机器人支撑相时的模型进行简化，其中1、3为当前的支撑腿，如图6所示。

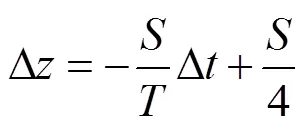
式中为步幅长度，m；为步行周期，s；∆为以当前支撑相为起点的步行时间，s。当1、3腿为支撑相时，取简化为五杆机构的四足机器人整体为研究对象，可得到力与力矩的平衡方程

注：G为机身质量，kg；Zb为四足机器人前进方向；M12, M32分别为前后足端对两大腿关节的转矩，N·m；N12, N32分别为大腿关节对机身的反作用力，N·m；M13, M33分别为前后足端对两小腿关节的转矩，N·m；N13, N33分别为地面对两足端的反作用力，N·m。

对式（10）、（11）进行连列求解可得到反作用力13和33的表达式为

现以四足机器人单腿为研究对象，在四足机器人直线运动时髋关节驱动力矩1=0。为了平衡地面对右前腿足端的支撑反力，须给大腿和小腿关节施加驱力矩12(N·m)和13(N·m)，保持力的作用效果不变。则四足机器人单腿支撑相时的各关节驱动力矩数学表达式如下。

5 动力学尺度综合分析

对于有确定任务需求和目标轨迹的四足机器人而言，考虑到关节驱动力矩峰值过大，会增加能量损耗，产生较大的力矩波动，降低了机器人运行时的平稳性，且减小电机的疲劳寿命[21-22]。因此设法降低四足机器人在目标轨迹上的驱动力矩峰值对于提高四足机器人动力学性能具有重要意义。

5.1 设计变量与目标函数

本文研究的目的是使四足机器人在目标轨迹上的驱动力矩峰值T(=1,2,3)下降，根据动力学公式（13）可知，在给定目标轨迹和步态参数下，影响各关节驱动力矩的因素为2、3，因此其设计变量为[2,3]。

本文属于多目标优化问题，通过改变腿部的尺寸参数可以得到四足机器人在整个运动周期上各关节的驱动力矩峰值。由于大腿和小腿关节受力不同，所以在实际过程中使四足机器人大腿和小腿关节同时满足驱动力矩峰值最大值最小是不可现实的。因此需要通过理想点法将多目标问题转化为单目标问题加以优化。取基于目标轨迹优化后的大腿与小腿驱动力矩最大值Max(2)和Max(3)中的最小值min(Max2)和min(Max3)作为理想点，利用最短距离理想点法将原多目标规划问题转化成如下单目标优化问题[23-25]，得到最终的目标函数为

5.2 约束条件

由于四足机器人是基于给定的目标轨迹进行运动，考虑到腿部尺寸过长和过短都会对四足机器人的稳定性、灵活性以及工作空间范围产生影响[26-28]，故需要先对腿部尺寸施加合理的范围约束。本文前期通过枚举法选取大量不同组合的杆长对结果进行初步对比验证，试验数据表明，选取2,3=[0.2,0.5](m)范围内，会使得最终的输出力矩相对合理有效。

由于本文使用D-H法进行运动学建模，所以在粒子群算法搜索的过程中会因不同杆长而出现奇异点，导致粒子群算法不会收敛到最优解。为保证数据的合理性、正确性，对目标函数施加以下约束条件：

式中min(Max2)、min(Max3)和min()均属于实数域，从而能够搜索到最优解。

5.3 优化分析

本文分2次进行优化，第一次初步优化是将腿部杆长L(=1,2,3)作为其设计变量，腿部各关节驱动力矩T(=1,2,3)作为适应度函数，并添加一定的约束条件，通过粒子群算法[29-30]进行优化，其参数设置如下：粒子数目=40，学习因子为1=2=2，最大权重max=0.9，最小权重min=0.4，迭代步数取1 000次，其适应度函数为=min(MaxT)(=1,2,3)，分别得到腿部驱动力矩T(=1,2,3)最大值最小的值，并以此作为理想点，各理想点分别对应2组杆长(2,3)和(2,3)。

第二次优化是将第一次优化得到的理想点运用理想点法将多目标函数转化为单目标函数[31]：

通过将第一次优化得到的2组杆长(2,2)和(3,3)作为粒子群算法搜索的约束条件，将构造的评价函数作为算法的适应度函数，再次运用粒子群算法，其参数设置同上，最终得到使得四足激光除草机器人腿部各关节驱动力矩最大值最小的一组杆长。

6 试验验证

6.1 优化求解

通过第一次运用粒子群算法得到支撑相时大腿关节驱动力矩最大值最小的理想点为min(Max(2))= 23.253 1 N·m，对应杆长为2=0.339 2 m，3=0.340 3m；小腿关节驱动力矩最大值最小的理想点为min(Max(3))= 75.708 6 N·m，对应杆长为2=0.340 1 m，3=0.339 6 m，其基于粒子群算法适应度与迭代次数的关系如图7所示。

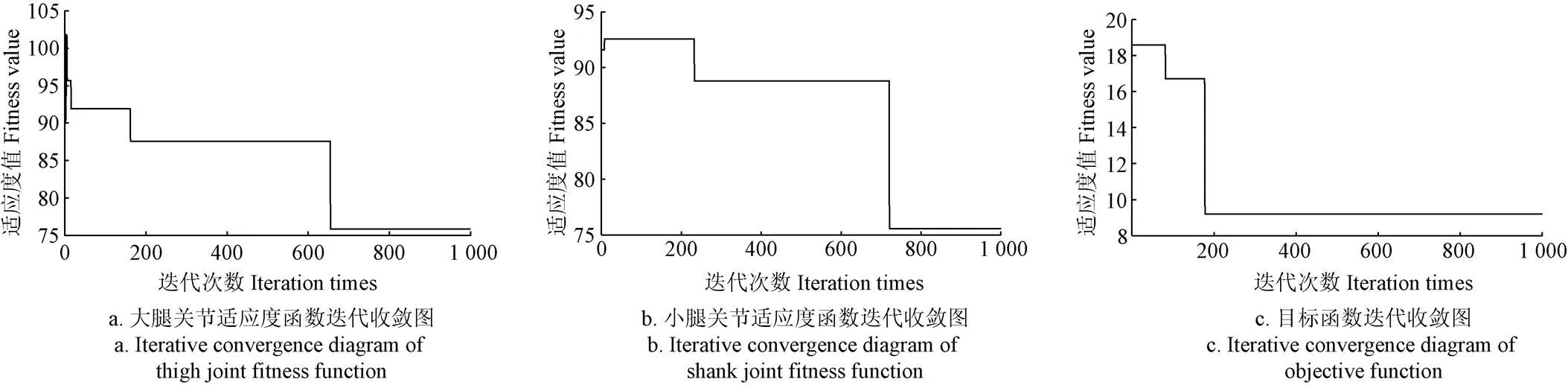
图7 各适应度函数与迭代次数关系图

将第一次优化得到的理想点带入评价函数min()中，再次运用粒子群算法在新的搜索区间中得到最优解min()=9.165 6，对应的最优杆长为2=0.340 1 m，3=0.340 0 m。其目标函数适应度值与迭代次数的关系如图7c所示。

6.2 结果分析

四足机器人优化前后的参数如表2所示。当选取最优杆长(2,3)=(0.340 1, 0.340 0)时，根据式（7）、（9）、（13）通过MATLAB进行仿真计算，得到在整个支撑相上腿部各关节驱动力矩优化前后变化曲线，如图8所示。由图8可知大腿关节驱动力矩峰值由优化前的24.552 6 N·m降至23.253 1 N·m，降幅为5.29%；小腿关节驱动力矩峰值由优化前的92.385 7 N·m降至75.708 6 N·m，降幅为18.05%。

表2 四足机器人优化前后结构参数

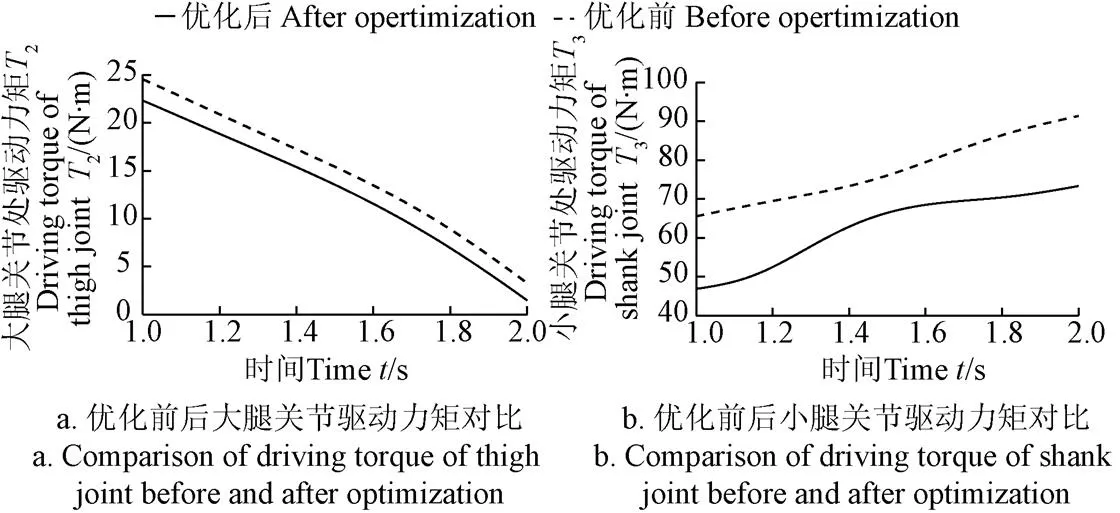
图8 优化前后腿部各关节驱动力矩对比

在不考虑能量损失等其他因素时，单腿支撑相在一个周期内所消耗的能量可表示为[31]：

式中P1为大腿关节驱动功率，N·m/s；P2为小腿关节驱动功率，N·m/s；为大腿关节角速度，rad/s；为小腿关节角速度，rad/s。再根据式（7）、（9）、（17）得到整个支撑相上腿部关节驱动力矩优化前后的功率对比，如图9a和图9b所示。由图10可知，优化后四足机器人的驱动功率下降，则电机功耗也随之下降。不考虑其他影响，优化后四足激光除草机器人的动力学性能和功耗得到明显改善。

6.3 优化结果验证

本文以得到的腿部最优杆长尺寸对其进行四足激光除草机器人的结构设计，并制造实物样机对结果进行验证。图10为设计的实物样机步态连续行走过程，其中图 10a为四足机器人初始位姿，此时左前腿和右后腿组成对角线，右前腿和左后腿组成另一组对角线；图10b为左后腿和右前腿作为支撑相，左前腿和右后腿作为摆动相同时向前迈进；图10c为左前腿和右后腿作为支撑相，右前腿和左后腿作为摆动相同时向前迈进，落地后回到初始位姿，此时四足机器人移动步长；图10d为四足机器人第二个周期时的步态，两组对角腿循环向前迈进实现了四足机器人对角小跑步态向前运动。实验测试结果如表3所示，则验证结果表明与优化前的实物样机相比，其运动性能得到明显的改善。

图10 实物样机trot步态下的行走过程

表3 四足机器人参数优化前后性能对比

7 结 论

1）本文以四足激光除草机器人腿部支撑相时，关节驱动力矩最大值最小化作为优化目标，以腿部尺寸参数作为其设计变量，提出了一种基于目标轨迹下的四足激光除草机器人动力学尺度综合方法。

2）在满足任务要求的情况下，规划了一条零冲击、且速度和加速度连续的复合摆线轨迹，并分析了在机身质量作用下的四足激光除草机器人在支撑相时的输出力矩变化情况。

3）运用理想点法将四足激光除草机器人腿部结构参数优化的尺度变量转化为粒子群算法的维度决策变量，得到了一组最优杆长(2,3)=(0.340 1, 0.340 0)，并对基于这组最优杆长下的四足机器人驱动力矩进行分析和验证。实验结果表明单腿的大腿关节驱动力矩峰值下降5.29%，小腿关节驱动力矩峰值下降18.05%，大幅降低了四足激光除草机器人的各关节驱动力矩峰值和能耗，验证了本文给定目标轨迹下的四足激光除草机器人动力学尺度综合方法的正确性和优越性，可为四足类的机器人动力学尺度综合提供参考。

[1]周福君，王文明，李小利，等. 摇杆式摆动型玉米株间除草装置设计与实验[J]. 农业机械学报，2018，49(1)：77－85.

Zhou Fuzun, Wang Wenming, Li Xiaoli, et al. Design and experiment of cam rocker swing intra-row weeding device for Maize[J]. Transactions of The Chinese Society for Agricultural Machinery, 2018, 49(1): 77－85. (in Chinese with English abstract)

[2]贾洪雷，李森森，王刚，等. 中耕期玉米田间避苗除草装置设计与实验[J]. 农业工程学报，2018，34(7)：15－22.

Jia Honglei, Li Sensen, Wang Gang, et al. Design and experiment of seedling avoidable weeding control device for intertillage maize[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 15－22. (in Chinese with English abstract)

[3]徐丽明，于畅畅，刘文，等. 篱架式栽培葡萄株间除草机自动避障机构优化设计[J]. 农业工程学报，2018，34(7)：23－30. Xu Liming, Yu Changchang, Liu Wen, et al. Optimal design on auto obstacle avoidance mechanism of intra-row weeder for trellis cultivated grape[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 23－30. (in Chinese with English abstract)

[4]柏龙，龙樟，陈晓红，等. 连续电驱动四足机器人腿部机构设计与分析[J]. 机器人，2018，40(2)：136－144.

Bai Long, Long Zhang, Chen Xiaohong, et al. Design and analysis of a leg mechanism for a continuous electrically-driven quadruped robot[J]. Robot, 2018, 40(2): 136－144. (in Chinese with English abstract)

[5]高峰，雷静桃，徐国艳. 四足步行机的对角小跑步态及能耗仿真分析[J]. 北京航空航天大学学报，2007，33(6)：719－722.

Gao Feng, Lei Jingtao, Xu Guoyan. Trot gait and energy consumption simulation of a quadruped robot[J]. Journal of Beijing University of Aeronautics, 2007, 33(6): 719－722. (in Chinese with English abstract)

[6]郑楚婷，宋光明，乔贵方，等. 具有主动腰关节的四足机器人在间歇对角步态下的姿态平衡控制[J]. 机器人，2007，38(6)：670－677.

Zheng Chuting, Song Guangming, Qiao Guifang, et al. Posture balance control of the quadruped robot with an waist joint during intermittent trot locomotion[J]. Robot, 2007, 38(6): 670－677. (in Chinese with English abstract)

[7]马宗利，朱彦防，刘永超，等. 四足机器人新型节能腿的设计与分析[J]. 东北大学学报，2016，37(4)：543－547.

Ma Zongli, Zhu Yanfang, Liu Yongchao, et al. Design and analysis of new energy-efficient legs for quadruped robots[J]. Journal of Northeastern University, 2016, 37(4): 543－547. (in Chinese with English abstract)

[8]雷静桃，王峰，俞煌颖. 四足机器人轨迹规划及移动能耗分析[J]. 机械设计与研究，2014，30(1)：29－34.

Lei Jingtao, Wang Feng, Yu Huangying. Analysis on trajectory planning and energy consumption of quadruped robot[J]. Machine Design & Research, 2014, 30(1): 29－34. (in Chinese with English abstract)

[9]李军，苗新聪，张晓宇. 四足机器人步幅、步频与扭矩和能耗关系研究[J]. 组合机床与自动化加工技术，2018，12(12)：10－14.

Li Jun, Miao Xincong, Zhang Xiaoyu. The research on effect of stride frequency and stride length on joint torque and energy cost in trotting of quadruped robot[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2018, 12(12): 10－14. (in Chinese with English abstract)

[10]郑坤明，张秋菊. 一种高速轻型化并联机器人尺度综合的研究[J]. 机械设计，2017，34(4)：29－38.

Zheng Kunming, Zhang Qiuju. Research on dimensional synthesis of high speed light-duty parallel robot[J]. Journal of Machine Design, 2017, 34(4): 29－38. (in Chinese with English abstract)

[11]鹿玲，张东胜，许允斗，等. 五自由度混联机器人尺度与结构优化设计[J]. 农业机械学报，2018，49(4)：412－419.

Lu Ling, Zhang Dongsheng, Xu Yundou, et al. Dimension and structure optimization design of 5-DOF hybird manipulator[J]. Transactions of The Chinese Society of Agricultural Machinery, 2018, 49(4): 412－419. (in Chinese with English abstract)

[12]王杰，管声启，夏齐霄. 手指康复外骨骼机器人的结构设计优化[J]. 中国机械工程，2018，29(2)：224－228.

Wang Jie, Guan Shengqi, Xia Qixiao. Structural design of finger rehabilitation exoskeleton robots[J]. China Mechanical Engineering, 2018, 29(2): 224－228. (in Chinese with English abstract)

[13]雷静桃，俞煌颖，王峰. 四足机器人对角小跑步态动态稳定步行足端非连续约束及动力学建模[J]. 中国机械工程，2015，26(5)：592－597.

Lei Jingtao, Yu Huangying, Wang Feng. Analysis on non-continuous constraints and dynamics modeling of quadruped robot dynamically stable walking with trot gait[J]. China Mechanical Engineering, 2015, 26(5): 592－597. (in Chinese with English abstract)

[14]郝仁剑，王军政，史大威，等. 基于速度矢量的四足机器人间歇步态规划方法[J]. 机器人，2016，38(5)：540－549.

Hao Renjian, Wang Junzheng, Shi Dawei, et al. Intermittent gait planning methon of quadruped robot based on velocity vector[J]. Robot, 2016, 38(5): 540－549. (in Chinese with English abstract)

[15]高炳微，王思凯，高元峰. 液压四足机器人单腿竖直跳跃步态规划[J]. 仪表仪器学报，2017，38(5)：1086－1092.

Gao Bingwei, Wang Sikai, Gao Yuanfeng. Single leg vertical hopping gait planning for hydraulic quadruped robot[J]. Chinese Journal of Scientific Instrument, 2017, 38(5): 1086－1092. (in Chinese with English abstract)

[16]韩宝玲，汪清强，贾燕，等. 提升四足机器人行走稳定性的对角步态规划方法[J]. 北京理工大学学报，2018，38(9)：917－920.

Han Baoling, Wang Qingqiang, Jia Yan, et al. Trot gait planning method for improving the stability of quadruped robot[J]. Transaction of Beijing Institute of Technology, 2018, 38(9): 917－920. (in Chinese with English abstract)

[17]何冬青，马培荪，曹曦，等. 四足机器人对角小跑起步姿态对稳定步行的影响[J]. 机器人，2004，26(6)：925－932.

He Dongqing, Ma Peisun, Cao Xi, et al. Impact of Initial stance of quadruped trotting on walking stability[J]. Robot, 2004, 26(6): 925－932. (in Chinese with English abstract)

[18]张志宇. 基于ADAMS的四足机器人虚拟样机仿真及刚柔耦合分析[D]. 哈尔滨：哈尔滨工业大学，2016.

Zhang Zhiyu. Virtual Prototype Simulation and Rigid-flexible Coupling Analysis of Quadruped Robot Based on ADAMS[D]. Harbin: Harbin Institute of Technology, 2016. (in Chinese with English abstract)

[19]Lei J T, Yu H Y. Dynamics analysis of bionic flexible body driven by pneumatic artificial muscle for quadruped robot[J]. Journal of shanghai Jiao Tong University, 2014, 48(12): 1688－1693: 1699.

[20]Rong X W, Song E, Li B. Joint driving forces calculation for a quadruped for a quadruped robot in sagittal plane motions[J]. Journal of Information and Computational Science, 2012, 9(12): 3413－3419.

[21]任东一，邵俊鹏，孙桂涛，等. 液压四足机器人机身扰动抑制及实验研究[J]. 机器人，2019，40(4)：163－171.

Ren Dongyi, Shao Junpeng, Sun Guitao, et al. Torso disturbance inhibition and experiment research of hydraulic quadruped robot[J]. Robot, 2019，40(4): 163－171. (in Chinese with English abstract)

[22]陈腾，李贻斌，荣学文. 四足机器人动步态下实时足底力优化方法的设计与验证[J]. 机器人，2019，41(3)：307－316.

Chen Teng, Li Yibin, Rong Xuewen. Design and verification of real-time plantar force optimization quadruped robots in dynamic gait[J]. Robot, 2019, 41(3): 307－316. (in Chinese with English abstract)

[23]蒋荣超，刘大维，王登峰. 基于熵权TOPSIS方法的整车动力学性能多目标优化[J]. 机械工程学报，2018，54(2)：150－158.

Jiang Rongchao, Liu Dawei, Wang Dengfeng. Multi-objective optimization of vehicle dynamics performance based on entropy weighted TOPSIS method[J]. Journal of Mechanical Engineering, 2018 54(2): 150－158. (in Chinese with English abstract)

[24]张良安，马演东，单家正，等. 4自由度含局部闭链式码垛机器人动力学优化设计[J]. 农业机械学报，2013，44(11)：336－341.

Zhang Liang’an, Ma Yandong, Shan Jiazheng, et al. Optimal dynamic design of 4-DOF palletizing robot with closed-chain[J]. Transactions of The Chinese Society of Agricultural Machinery, 2013, 4(11): 336－341. (in Chinese with English abstract)

[25]赵海鸣，蒋彬彬，李密. 基于拓扑优化与多目标的机床底座结构设计[J]. 机械设计与研究，2018，34(4)：100－105.

Zhao Haiming, Jiang Binbin, Li Mi. Structure design of machine tool based on topology optimization and multi-objective optimization[J]. Machine Design and Research, 2018, 34(4): 100－105. (in Chinese with English abstract)

[26]沈惠平，李菊，王振，等. 基于结构降耦和运动解耦的并联机构拓扑结构优化及性能改善[J]. 机械工程学报，2017，53(19)：100－105.

Shen Huiping, Li Ju, Wang Zhen, et al. Topology structure optimization and performance improvement for parallel mechanisms based on structure coupling-reducing and motion decoupling[J]. Journal of Mechanical Engineering, 2017, 53(19): 176－186. (in Chinese with English abstract)

[27]丁良宏. BigDog四足机器人关键技术分析[J]. 机械工程学报，2015，51(7)：1－22.

Ding Lianghong. Key Technology analysis of BigDog quadruped robot[J]. Journal of Mechanical Engineering, 2015, 51(7): 1－22. (in Chinese with English abstract)

[28]孙龙飞，房立金. 机械手臂结构设计与性能分析[J]. 农业机械学报，2017，48(9)：402－410.

Sun Longfei, Fang Lijin. Design and performance analysis of novel robotic arm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(9): 402－410. (in Chinese with English abstract)

[29]张良安，万俊，谭玉良. Ahut-Delta 并联机构改进混沌粒子群算法尺度综合[J]. 农业机械学报，2015，46(8)：344－351.

Zhang Liang’an, Wan Jun, Tan Yuliang. Dimensional synthesis of ahut-delta parallel mechanism based on improved chaotic particle swarm algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(8): 344－351. (in Chinese with English abstract)

[30]王强，张培林，玉怀光，等. 基于多目标粒子群算法的稀疏分解参数优化[J]. 振动与冲击，2017，36(23)：45－50.

Wang Qiang, Zhang Peilin, Yu Huaiguang, et al. Parametric optimization of sparse decomposision based on multi-objective particle swarm optimization algorithm[J]. Journal of Vibration and Shock, 2017, 36(23): 45－50. (in Chinese with English abstract)

[31]刘建，葛世荣，朱华，等. 基于多目标优化的矿用救援机器人动力匹配[J]. 机械工程学报，2015，51(3)：18－28.

Liu Jian, Ge Shirong, Zhu Hua, et al. Mine rescue robot power matching based on multi-objective particle swarm optimization[J]. Journal of Mechanical Engineering, 2015, 51(3): 18－28. (in Chinese with English abstract)

Optimization of leg structure parameter of quadruped laser weeding robot

Zhang Liang’an1, Tang Kai1, Zhao Yongjie2※, Wang Xiaoyi1,Yu Dazhuang1, Lu Xinjian3, Wang Xiang1

(1.243000;2.515063;3.,528226,)

Robot has been increasingly used in weeding. Taking the quadruped laser weeding robot as an example, this paper presents a method to optimize its four legs using the dynamic scale synthesis. The objective of the optimization was the lengths of the legs, in which, prior to optimizing the driving torque of the joint in each leg, we first optimized the driving torque of the leg based on the load it was required to take. The laser weeding robot used compound cycloid trajectory to plan its trajectory, which is ready for optimizing the driving torque of the joint in the rear leg. The optimization focused on the driving force moment on both the thigh joint and the calf joint, for which obtained a set of optimal thigh bar lengths and calf bar lengths. We first calculated the foot trajectory and the gait parameters of the robot, and then used the thigh joint force moment, the calf joint driving force moment and different leg rod lengths to maximize the dynamic target; the dimensional parameters of the legs were also taken as design parameter in the multi-objective constraint optimization. After the thigh joint driving force moment and the calf joint driving moment were firstly optimized using the particle group algorithm, the maximum torque of the leg joints within the each group of the rods was calculated under a given target trajectory by combining the leg sizes. Based on the smallest set of driving force moments, we found the maximum and minimum driving torque of each joint in the target trajectory, which was further optimized using the ideal dot method and the particle group algorithm. This transformed the multi-objective optimization to a single-objective optimization. These two-step optimizations allowed us to obtain the leg length in the group of optimal four-legged laser weeding robots. We verified the optimal results against experiments. The results showed that the optimized four-legged laser weeding robot significantly improved its dynamic performance compared to that without optimization. It was also found that the optimization reduced the maximum thigh joint driving force by 5.29% and the maximum driving force in the calf joint by 18.05%. The comprehensive methods presented in this paper cannot only help developing four-legged laser weeding robot prototype, but also provide references for studying driving force moment and energy consumption of four-legged robot.

quadruped robot; optimization; dimensional synthesis; particle swarm optimization

张良安，唐 锴，赵永杰，王孝义，余大壮，卢新建，王 祥. 四足激光除草机器人腿部结构参数优化[J]. 农业工程学报，2020，36(2)：7－15.doi：10.11975/j.issn.1002-6819.2020.02.002 http://www.tcsae.org

Zhang Liang’an, Tang Kai, Zhao Yongjie , Wang Xiaoyi, Yu Dazhuang, Lu Xinjian, Wang Xiang. Optimization of leg structure parameter of quadruped laser weeding robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(2): 7－15. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.02.002 http://www.tcsae.org

2019-10-24

2019-11-04

安徽省重点研究与开发计划项目（201904b11020030）；广东省普通高校省级重大科研项目—基础研究重大项目及应用研究重大项目（自然科学类）（2017KZDXM036）；佛山市科技创新团队专项项目资助（2018IT100052）

张良安，博士，教授，主要从事机器人技术及应用研究。Email：robotlab@ahut.edu.cn

赵永杰，博士，教授，主要从事机器人技术与机器设计研究。Email：meyizhao@stu.edu.cn

10.11975/j.issn.1002-6819.2020.02.002

TP242.6

A

1002-6819(2020)-02-0007-09