混纺纱的强伸性能分析
2020-11-30周镭,孔聪
周 镭,孔 聪
(1.山东省纺织科学研究院,山东 青岛266032;2.山东省特种纺织品加工技术重点实验室,山东 青岛266032;3.山东联润新材料科技有限公司,山东 枣庄277100)
混纺纱是由2种或2种以上不同种类的纤维纺制而成的,由于其性能综合了2种或2种以上不同纤维的优点,相互取长补短,满足了产品的不同需求,应用日趋广泛。混纺纱的性能与混纺比及组分纤维的性能关系密切,如何根据组分纤维的强伸性能确定合理的混纺比,以获得质量优异的混纺纱意义重大。已有研究对混纺纱的强度和伸长建立了理论模型[1],导出了混纺纱强度和伸长与混纺比及组分纤维的强伸性能的理论表达式[2]。本文介绍了混纺纱强度和伸长的理论模型,并采用实例对其进行了分析验证。
1 混纺纱的强伸性
1.1 混纺纱强度理论模型
当采用2种拉伸性能不同的纤维混纺成纱时,由于它们在断裂伸长率上的差异,导致其断裂具有不同时性[3]。为简化计算,假设:(1)混纺纱中的纤维混合均匀;(2)纱线被拉伸时,纤维间没有滑移,即纱线断裂是由纤维断裂引起的;(3)纤维断裂后不再对纱线强力做出贡献。在此基础上分析,当拉伸双组分混纺纱时,起初是两组分共同承担外力,纱中断裂伸长数值低的纤维组分率先断裂;随后,另一组分要承受已断裂的纤维组分所承受的额外负荷。而该组纤维能否承受此额外负荷,要看其拉伸性能及混纺比。
假设A 和B是2种不同断裂伸长的纤维,纤维A的断裂伸长小于纤维B,两者混纺成纱后,其各自成纱的拉伸曲线如图1所示。当纱线受到拉伸达到组分A的断裂伸长时,A 组分将断而未断,此时所受强力的强力可按式(1)进行计算:

其中,SA是由纤维A纺制的纯纺纱的断裂强力;为达到纤维A 的断裂伸长时,B组分承受的强力;a、b分别是纤维 A 和纤维B 的混纺比(%)。继续拉伸,A 组分断裂,所有外力均由B 组分承担。此时,B组分所能承担的最大强力为式(2):

SB是由纤维B纺制的纯纺纱的断裂强力。
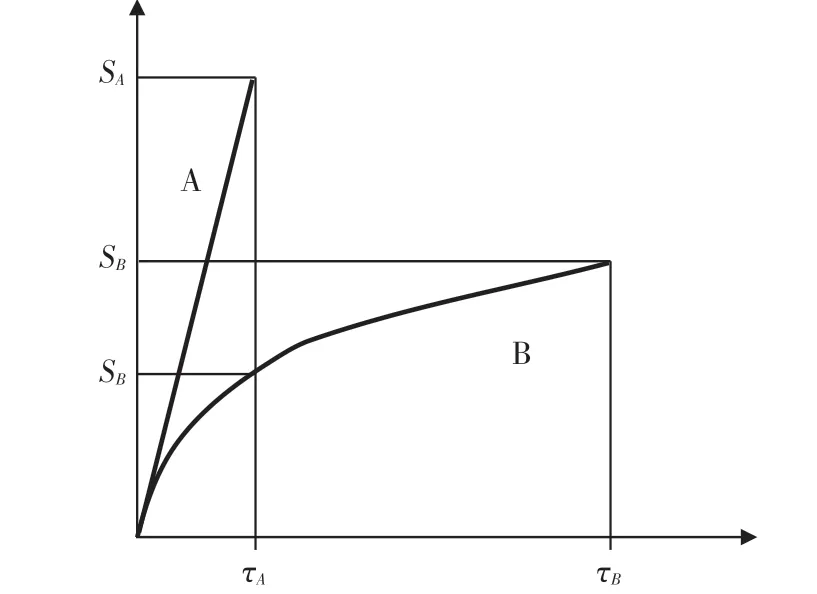
图1 双组分A、B纤维纯纺纱的拉伸曲线
由式(1)、式(2)可知,S1、S2与混纺比相关。对双组分纤维纺制的混纺纱来说,其断裂强力总是S1、S2中的最大值,即式(3)。

混纺纱强力随混纺比的理论变化曲线如图2中折线ACB所示。其中,C点为2种纤维混合纺成纱所具有最小断裂强力的临界点,对应的临界混纺比bc可由S1=S2计算得到:


图2 混纺纱断裂强力和混纺比的关系曲线
该理论模型可用来预测混纺纱的强度,并设计合理的混纺比避免混纺纱强力极低值,对实际生产有一定的指导意义。
1.2 混纺纱伸长率理论模型
当采用2种纤维A 和B 混纺时,若伸长较大的B组分的混纺比小于临界混纺比bc,则伸长较小的A 组分的断裂作用决定了整个混纺纱的断裂,即此时混纺纱的断裂伸长为εA。当B组分的混纺比b逐渐增大到大于bc时,A 组分完全断裂后,混纺纱尚未断裂,剩余的B组分还可承受张力继续伸长,此时,混纺纱的伸长ε>εA。随着B组分含量继续增加,伸长率继续增大,最后当b达到100%时,混纺纱的伸长率则完全达到B组分的伸长率εB[4]。 由此可作出混纺纱断裂伸长率与混纺比的关系曲线,如图3所示。
由图3的曲线可以得出双组分混纺纱的断裂伸长率的理论计算式为:

可以看出,采用伸长率大的纤维与伸长率小的纤维进行混纺,混纺纱的伸长率并不是立即增加,而是当伸长率大的纤维的混纺比超过临界混纺比时才逐渐增加。利用式(5),只要知道每一组分的拉伸曲线就可以从理论上计算出混纺纱的断裂伸长率[5]。
混纺纱强伸性的理论模型对实际生产有一定的指导意义,可以通过实例验证2个模型的有效性。
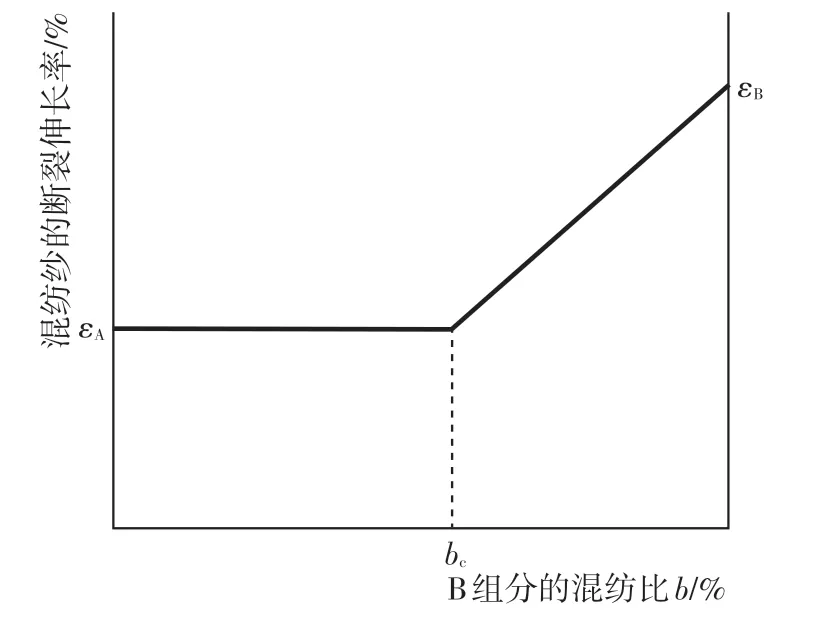
图3 混纺纱断裂伸长率和混纺比的关系曲线
2 实例验证
2.1 拉伸细化羊毛/羊绒混纺纱
以不同混纺比纺制了32 tex细化羊毛/羊绒混纺纱,根据GB/T 3292—1997 测试混纺纱的强伸性能。试验仪器为YG061F 型电子单纱强力仪,测试大气条件:温度(20±2)℃,相对湿度(65±3)%。
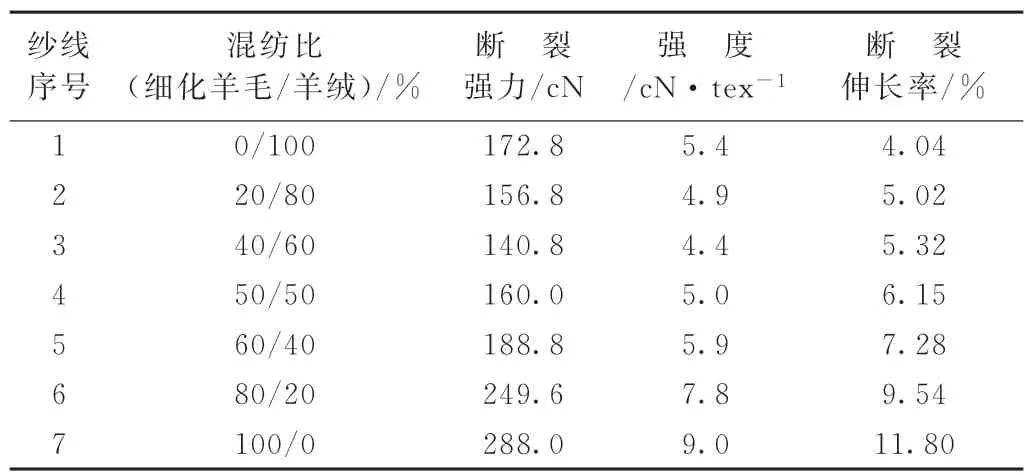
表1 不同混纺比纱线的强度指标
根据理论模型绘制细化羊毛/羊绒混纺纱强度曲线,并作出实测纱线强度与混纺比的拟合曲线,如图4所示。拟合曲线表达式为:Y=7.29294-0.08434X+5.44818×10-4X2,R2=0.96153。
由图4所见,将混纺纱实测强度拟合曲线与理论模型曲线相比较,它们的变化规律基本一致。而实测强度较大,是因为理论模型设计忽略了纤维间滑移以及2种纤维间的交互作用等因素,也未考虑同组纤维间断裂伸长率的变异[6]。根据理论模型计算的临界混纺比结果为41%,实测强度也是在细化羊毛的含量为40%时出现了最低值,符合理论模型。
根据表1的数据绘制出细化羊毛/羊绒混纺纱线断裂伸长率与细化羊毛含量的关系曲线,同时根据理论模型绘制模型曲线,如图5所示。
从图5可以看出,实测混纺纱的断裂伸长率与理论模型的总体变化趋势趋于一致。当细化羊毛含量低于40%时,混纺纱的断裂伸长率较低,实测曲线趋于平直,这是由于羊绒纤维的断裂伸长率占主导决定了混纺纱的断裂伸长率;当细化羊毛含量高于40%时,随着其含量增加,混纺纱的断裂伸长率大幅提高,这是由于羊绒断裂后,细化羊毛继续伸长,混纺纱继续伸长。实测的断裂伸长率高于理论值,原因在于理论模型忽略了纤维间的滑移因素,且忽略了即便是同种纤维,其断裂伸长率间也会存在着差异。由图5也可以看出,当混纺比未达到临界混纺比时,混纺纱的断裂伸长率不是不增加,而是增加的较为缓慢。

图4 混纺纱强度与混纺比的关系
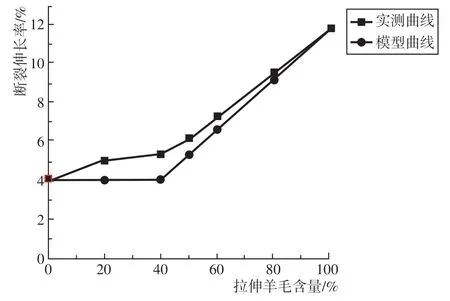
图5 混纺纱断裂伸长率与细化羊毛含量的关系
2.2 竹浆纤维/棉混纺纱
以不同混纺比纺制14.5 tex竹浆纤维/棉混纺纱,测试混纺纱的强伸性。试验条件:YG061-PC 型电子单纱强力仪,温度20 ℃,相对湿度65%;测试参数:隔距500 mm,预加张力0.5 c N/tex,拉伸速度500 mm/min,试样根数60根。
由纯棉纱和纯竹浆纱的拉伸曲线可知,S′B约为110 c N,即强度约为7.59 c N/tex。据此,作出混纺纱强度的模型曲线及实测曲线如图7所示。
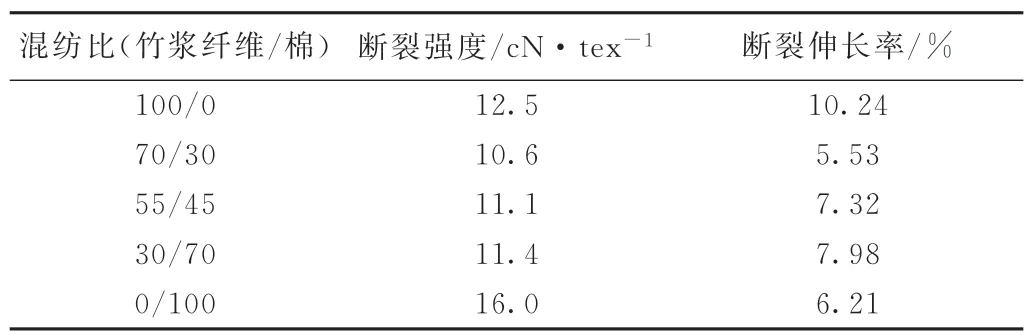
表2 竹浆纤维/棉混纺纱强度测试结果

图6 纯棉纱和纯竹浆纱的拉伸曲线
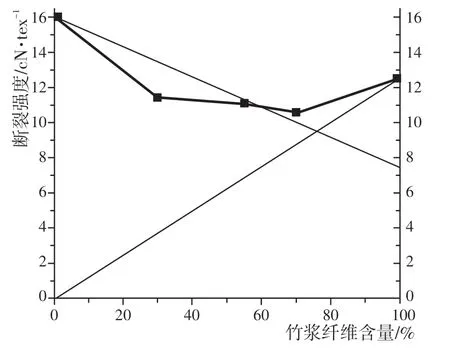
图7 混纺纱强度与混纺比的关系
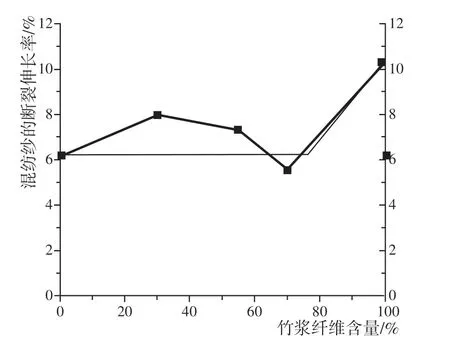
图8 混纺纱断裂伸长率和混纺比的关系
由图7可以看出,混纺纱实测强度随混纺比的变化趋势基本符合理论模型。随着竹浆纤维的含量增加,混纺纱的强度先下降至最低值,然后上升。根据理论模型计算的临界混纺比约为76.5%,而在竹浆纤维含量为70%时,实测强度达到最低值,与理论模型基本吻合。
根据表2绘制混纺纱的断裂伸长率与混纺比的关系曲线,并根据理论模型绘制模型曲线,如图8所示。
从图8可以看出,随着竹浆纤维在纱中含量的提高,混纺纱的断裂伸长先是略有增加,当竹浆纤维的含量达到临界混纺比时,混纺纱断裂伸长率大幅上升。总体趋势与理论模型大致一致,但并不完全吻合,而是有一些差异,但所反应的变化规律是一致的[7]。
2.3 聚乳酸/棉混纺纱
采用不同的混纺比纺制出了一系列的聚乳酸/棉混纺纱,按理论模型预测各种混纺比的纱线强力[8],并实测混纺纱强力。

表3 混纺纱强力预测值与实测结果
根据实测结果,SA=284.8 c N,SB=324.8 c N,根据两者的拉伸图可找出S′B=166 c N。由此作出混纺纱强力的模型曲线与实测曲线,如图9所示。
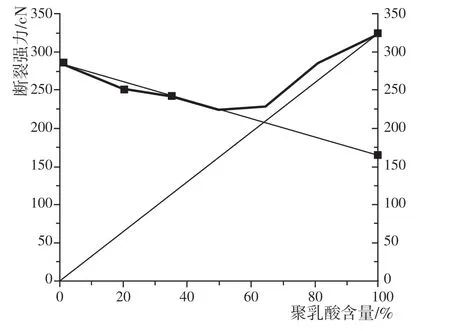
图9 混纺纱强力与混纺比的关系
由图9及预测强力和实测强力比较可知,聚乳酸/棉混纺纱的强力与混纺比的关系符合理论模型,随聚乳酸含量增加,混纺纱强力先下降达到最低值,然后上升。由理论模型计算可知临界混纺比bc为64%,而实测强力在聚乳酸含量为65%时达到了最低值,与理论模型有极好的吻合程度。
根据表3可做出混纺纱断裂伸长率与混纺比的关系的实测曲线和理论曲线,如图10所示。

图10 混纺纱断裂伸长率与混纺比的关系
由图10可以看出,混纺纱的断裂伸长率随着聚乳酸纤维含量的提高,先是基本保持不变,当达到某一混纺比时开始缓慢增加,当达到临界混纺比时快速上升。总体变化趋势与理论模型相一致,但并不完全吻合,未达到混纺比临界点之前,混纺纱的断裂伸长也有所增加。
3 结论
(1)混纺纱强力的理论模型与实测混纺纱强力基本符合,该模型能够较好地反应混纺纱强力随混纺比的变化趋势,可用来指导实际生产。
(2)混纺纱伸长率的理论模型虽与实测混纺纱伸长率间存在差异,但也能反应混纺纱的断裂伸长率随纤维混纺比的变化规律。
(3)混纺纱的断裂伸长率在临界混纺比之前并不是保持不变,而是也有所增加,只不过增加的比较缓慢,故临界混纺比bc应设置一个置信区间。
