500 kV垂直排列双回紧凑型线路舞动不平衡张力计算

杨 力 梁盼望 李 辉 蒋少波

（中国能源建设集团湖南省电力设计院有限公司，湖南长沙410007）

0 引言

随着我国经济社会快速发展，输电线路走廊日益紧张，在路径走廊拥挤地区采用紧凑型输电方案具有巨大的社会效益和经济效益[1]。因紧凑型线路通过压缩导线相间距离来压缩输电线路走廊，因此存在相间距离小于常规输电线路的固有缺陷，发生舞动后损害将更严重。

舞动引起倒塔的原因主要有两个，其一是导线舞动引起的长时间持续振动，振动张力较大，引起铁塔螺栓松动，导致导线挂点和横担部位的螺栓松动、脱落；其二是导线舞动张力较大，使得铁塔承受很大的舞动不平衡张力作用。因此，本文针对500 kV垂直排列双回紧凑型线路开展舞动不平衡张力计算，对铁塔进行安全校核，确保线路在舞动区的安全运行。

1 计算模型

本文研究以500 kV垂直排列双回紧凑型线路为例，导线采用4×JL3/G1A-630/45钢芯铝绞线，分裂间距500 mm，地线采用2根OPGW光缆，两相导线水平距离为7.7 m，回路间层间距离18.6 m。

2 舞动的频率特性

导线的舞动频率特性计算公式如下：

式中：f为舞动的频率（Hz）；T为导线舞动时的初张力（N）；m为导线的单位长度重量（kg/m）；n为半波数即舞动阶次，本文取2；l为档距。

导线为4×JL3/G1A-630/45钢芯铝绞线，最大使用应力85MPa，设计风速27 m/s，覆冰厚度15 mm（中冰区），代表档距取400 m，档距为500 m，舞动时风速10 m/s，舞动时覆冰5 mm，舞动时气温-5 ℃，舞动阶次取2，导线初张力38 788 N，覆冰导线重量2.617 kg/m，导线舞动频率为0.243 Hz，每分钟舞动14.6次。

3 导线舞动张力计算方法

3.1 能量平衡法

假定导线应力应变特性符合胡克定律，忽略杆塔形变和绝缘子金具串对导线的影响，假设导线抗弯刚度、抗扭刚度和剪切刚度均足够小，导线为理想柔索，仅考虑导线在Y轴方向的振动，不计阻尼，导线任一点在t时刻舞动位移为：

式中：i为舞动模态个数；s为舞动模态总数；x为导线在Y轴方向的坐标；t为时间；Foi为第阶ni导线舞动时的振幅；ni为导线舞动阶数；l为档距；ωi为第ni阶舞动的圆频率；ψi为第ni阶舞动的初始相位。

导线舞动通过风力获得能量产生动能和位能及弹性变形能。

动能：

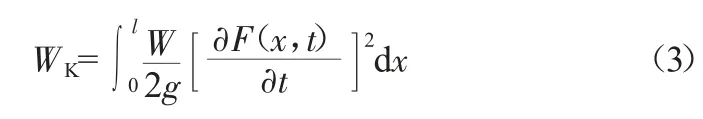
位能：

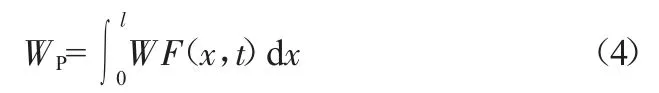
弹性变形能：

根据能量守恒原则有WK=WP+WE，可以解得舞动张力为：

当n为奇数，sin（ωit+ψi）=-4g/（niπFoiωi2）时，最大舞动张力为：

当n为偶数，cos（ωit+ψi）=±1时，最大舞动张力为：

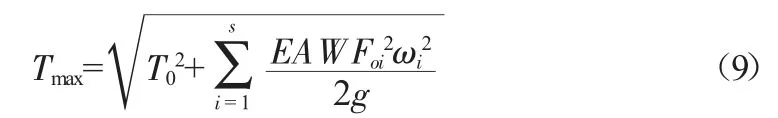
式中：T0为舞动前导线张力（kN）；W 为舞动时导线重量（kN/m）；A为导线截面（mm2）；E为导线弹性模量（kN/mm2）；g为重力加速度；Foi为第ni阶导线舞动振幅；ni为导线舞动阶数；ωi为第ni阶舞动的圆频率。

3.2 数值模拟法

因铁塔—导线—绝缘子金具串系统十分复杂，数字模拟法采用有线元模型计算，需对导线、结构和连接金具细化建模，在一般舞动幅值情况下，杆塔刚度和谐振频率远大于导线系统，可对杆塔结构进行简化建模处理，只考虑其连接性能，为便于分析，杆塔采用固定边界模型。对导线结构静力分析计算时采用杆或索单元，仅考虑三个方向的自由度，对于动力分析，绝缘子和金具的扭转自由度往往不可忽略，实际建模过程导线系统采用非线性曲线梁单元进行离散建模。

大量的舞动观测表明，舞动的响应特征呈现低频段的单阶模态振动或数个模态叠加的耦合振动，故数值模拟计算过程荷载处理为直接施加单个或多个耦合叠加的舞动驻波。

导线舞动呈现为大振幅、低频率动态响应过程，在一般舞动幅值条件下，忽略材料非线性影响，只考虑大变形的几何非线性，迭代算法采用现有成熟软件ANSYS实现，求得系统的张力变化。

3.3 长度变化法

长度变化法能够直接体现出档距和挂点高差对舞动张力的影响，计算模型如下：

舞动前的导线坐标：

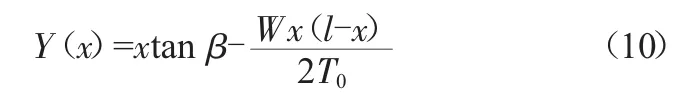
舞动前的导线长度：

舞动时的导线长度：

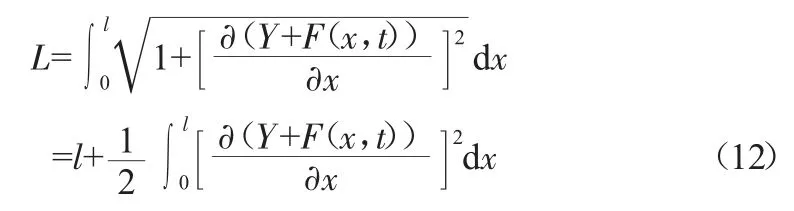
根据胡克定律，导线舞动张力为：

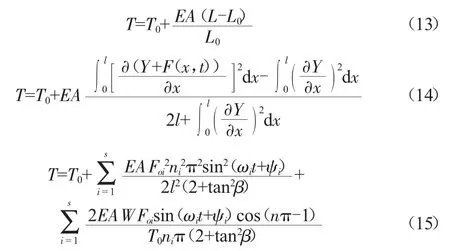
当n为奇数，且sin（ωit+ψi）=-1时，最大舞动张力为：

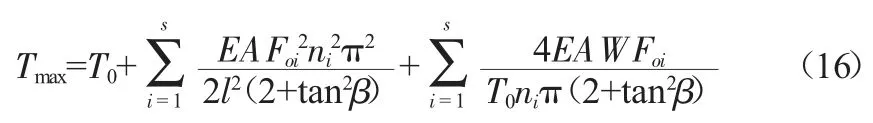
当n为偶数，且sin（ωit+ψi）=±1时，最大舞动张力为：

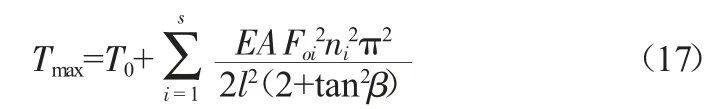
式中：T0为舞动前的导线张力（kN）；A为导线的截面积（mm2）；E为导线的弹性模量（kN/mm2）；Foi为第ni阶导线舞动的振幅（m）；ni为导线舞动的阶数；β为导线的高差角β=tan-1（h/l）。

4 简化算法

本文采用长度变化计算导线最大舞动张力。设定舞动阶数为偶数；一次舞动时档距中只有一个波形，可不考虑多个波形的耦合叠加，假定s=1、ni=1；因舞动大多发生在平丘地带，故可假定舞动的线路无高差；得到长度变化法的简化计算公式如下：

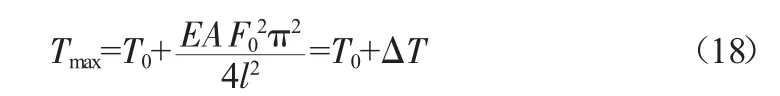
式中：T0为舞动前的导线张力（kN）；A为导线的截面积（mm2）；E为导线的弹性模量（kN/mm2）；F0为导线的舞动振幅（m）；l为档距（m）；ΔT为舞动时不平衡张力（kN）。

舞动时气温取-5 ℃，平均风速15 m/s，覆冰厚度5 mm，计算可得到导线的弧垂Fc，导线舞动时幅值取F0=0.2Fc，导线向上舞动的幅值取a1=0.8F0，导线向下舞动的幅值取a2=0.2F0。

引起舞动倒塔的主要原因是舞动时导线不平衡张力过大，直线塔由于两侧舞动方向差异，考虑舞动不平衡张力相互抵消约20%。

直线塔舞动时的不平衡张力：

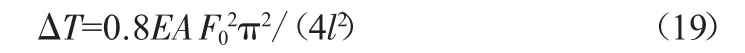
耐张塔舞动时的不平衡张力：

5 计算结果

导线舞动不平衡张力计算结果如表1所示。

表1 导线舞动不平衡张力计算结果

6 结语

本文采用长度变化法计算导线舞动不平衡张力，结果可见，随着风向与线路夹角的增大，导线舞动幅值明显增大，使得导线舞动不平衡张力快速增加。当风向与线路的夹角小于55°时，导线舞动不平衡张力小于15%；当风向与线路夹角大于55°时，导线舞动不平衡张力大于15%，可能造成舞动倒塔，需要安装防舞装置抑制导线舞动。