走进平均数，推开统计门

芦建章

平均数是小学阶段重要的统计的量，它能反应一组数据的真实情况或一般水平，人们经常可以用它来判断和预测后面将要发生的事。

在传统教学中，平均数是作为一种典型应用题进行教学的，主要侧重于对给出数据的计算，求其平均数;在教学上通过计算平均数理解平均数意义，容易将平均数的学习演变成一种简单的计算技能的学习。如果用新课标的眼光来看，传统教学中的平均数是作为“数与代数”领域进行教学的。

因此，教师在课堂上，不但要在新授环节中揭示平均数统计上的意义，培养学生统计的意识，更要通过练习，渗透统计的概念，传递统计的思想，训练统计的思维，传授最基本的统计方法，让学生感受到平均数是统计的范畴，真正走进统计的大门。下面，结合笔者自己的实际教学活动，谈谈平均数练习设计上的几点建议。

一、抓平均数意义本质设计练习，渗透统计的概念

既然平均数的本质属性是“统计”，那么平均数的练习理所当然应反映统计的内容，要从平均数统计意义的角度设计练习。从统计的角度看，求“**平均数”，就应收集两方面的数据：总数量与总份数，而且这两方面的数据是要相对应的，这样的设计才能突出统计的本意，才是比较合理恰当的练习。

（一）杜绝出现非平均数意义的练习

如：王司机开机，5小时行驶400千米。平均每小时行驶多少千米？

又如：买3千克苹果需要7.8元。平均每千克多少元？

此类练习，从问题来看，好像都是在求平均数，其实不是在教学怎样求平均数，而是在教学解决一般数量关系的问题。像上面的两道题目，就是解决“路程÷时间=速度”“总价÷数量=单价”的一般数量关系的练习题。

（二）避免出现似是而非的练习

如：小明买了5本书用了70元，那么平均每本书是多少元？

像这样的练习就似是而非了。如果这5本书是相同的书，那么此题又回归到了解决一般数量关系问题的练习了果这5本书是不同价格的书，才是计算平均数的练习题。我们不防把上题改为：

小明買《新华字典》用了18元，买《格林童话》用了12元，买《小作家》用了10元，买《翻转数学》用了25元，买《海洋世界》用了5元。平均每本书是多少元？

这样一改，就是一道计算平均数的练习了。

在设计平均数练习时，我们应该还平均数的本来面目，摒弃传统的非平均数意义、似是而非的平均数问题，换成学生比较熟悉、具有现实意义的统计内容，让平均数回归到统计的范畴。

二、以解题策略的多样性设计练习，训练统计的思维

（一）加强“移多补少”的练习

求平均数常用的有两种方法：一是“总数量÷总份数=平均数”，二是“移多补少”。一般情况下，我们都会选择“总数量÷总份数=平均数”进行教学。因为教材中的练习设计基本上也是采用这种方法来计算平均数的。而相对于“移多补少”的练习，不管是教材编排上，还是在平常的公开课、教研课的练习设计上，都是少而又少的。事实上，利用“移多补少”求平均数，能使学生进一步理解平均数的意义，进而明白“总数量÷总份数=平均数”是对“移多补少”的一种简便计算。因此，在课堂教学中，应加强“移多补少”的练习设计。

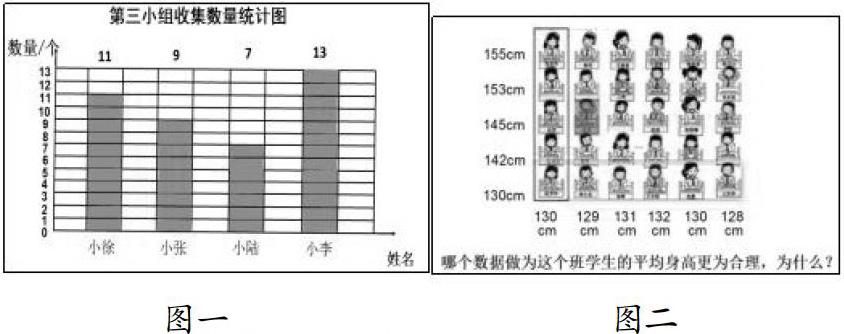
在课堂教学中，笔者就多次设计了有关“移多补少”法的练习，以强化学生对这一方法的掌握、运用。如在讲解例题中的“移多补少法”后，马上适时加入了相应的练习（图一）——用移多补少法，求第三组同学收集矿泉水瓶的成绩，进行模仿练习;在巩固提高环节，求班级学生平均身高时（图二），也让学生利用移多补少法求平均数。在多次运用中，加深对“移多补少法”的理解。

（二）解题策略的选择性

上面已提到平均数常用的方法：一是“总数量÷总份数=平均数”，二是“移多补少”。一般情况下，我们都会选择第一种，但并非第一种是最简单的。

上面图四中，第一行的平均身高可选择“移多补少法”更为方便，而第一列的平均身高用“总数量÷总份数=平均数”则更为简便。当碰到大数据时，我们还可选择以最少量为标准，把多出的量平均分……因此，在教学求平均数过程中，我们要善于利用练习，根据实际情况，训练学生选择恰当的解题策略，这也是统计思维的培养。

三、从学以致用角度设计练习，传授统计的方法

数学源自生活，又服务于生活。因此，教学了平均数后，教师要善于利用平均数的意义，向学生解释生活中的平均数;能让学生根据生活实际，判断平均数的合理性;并能学以致用，运用统计最基本的方法，解决生活中的平均数问题。

（一）平均数的现实性

在学生知道了平均数的意义，掌握了平均数的计算方法后，老师让学生列举生活中的平均数，并把学生课前收集到的数据进行展示：2017年全国人均收入61658元，人均住房面积40.8平方米，人均寿命76.7岁，男性人均身高167.1cm，女性平均身高155.8cm……引导学生说一说这里面的每个数据分别表示什么，再次重温平均数的意义，使得学习的数学知识与现实生活密切相连，在潜移默化中培养了学生留心观察生活的习惯，提高了学习数学知识的积极性。

（二）平均数的合理性

从统计的角度看平均数，平均数必须是能代表一组数据（或物）的整体水平，所以选择的数据必须是有意义的，具有代表性、全面性的。

在计算出上题（图二）第一行与第一列的平均数后，老师设计了这样的一个问题：

请你说说用哪个数据作为这个班的平均身高更为合理，为什么？

生1：用第一列的平均数145cm比较合适。

生2：我也认为用第一列的平均数做全班的平均身高比较合理。因为第一行的6位同学都坐第一排的，按我们班级的情况来看，第一排的同学身高比较矮;而第一列5位同学身高有高的，也有矮的，比较全面;所以用145cm作为全班学生的平均身高更为合理。

通过学生的反馈可知，学生不仅能选择合适的方法计算平均数，还理解了平均数的合理性——平均必须是能代表一组数据的整体水平。

（三）平均数的样本性

在计算平均数时，如果求出的平均数是所有研究对象全部数据求出的，就是总体平均数;但我们在生活中所接触到的很多平均数，是抽取一部分数据来求出平均数，即样本平均数。如上面学生收集到的一些平均数：2017年全国人均收入61658元，人均住房面积40.8平方米，人均寿命76.7岁，男性人均身高167.1cm，女性平均身高155.8cm……这些平均数是抽取一些有代表性、全面性的，有意义的数据进行统计求出平均数的，就是统计的样本平均数。

在学生明白了各个平均数据意义后，再设计拓展练习，学生不仅知道了求总体平均数的方法，而且通过教师及时补充的样本平均数知识，还明白了求样本平均数的最基本的方法，真正达到了联系生活，学以致用的目的。

四、从教学形式丰富上设计练习，传递统计的思想

平均数既然是统计与概率领域的内容，就离不开统计的素材。在课堂教学中，为了向学生传递平均数是统计的思想，笔者在练习设计时，给学生呈现了多种形式的统计数据，除有文本描述形式的求平均数外，还有从统计表中收集数据来求平均数的，更有从统计图中分析数据来计算平均数的。多种形式的统计素材，不仅丰富了课堂教学内容，素材的呈现方式，给学生以视觉上的有效刺激，也在潜移默化向学生传递：平均数是统计的重要内容;将平均数问题从简单的数学文本中解放出来，培养了学生从多方面分析、理解数据，发现问题，并解决问题的能力。

总之，平均数是统计学的前置知识，教师在设计教学时，要以平均数的本质属性“统计”为前提，设计科学适合的练习，让平均数教学散发出统计的气息和味道。