湖南杉木人工林单木干形特征及影响因子研究

许冰冰,边更战,易 烜,朱光玉,齐战涛,吕 勇

(1.中南林业科技大学,长沙 410004； 2.中部林业产权交易服务中心,长沙 410007；3.湖南省青羊湖国有林场,长沙 410600)

0 引言

树干的形状通称干形,干形一般分为饱满、通直、弯曲、尖削和主干是否明显之分,造成树木间干形差异的原因,除遗传性、年龄和枝条着生情况等内因的影响外,还受立地条件、气候因素、林分密度和经营措施等外因的影响[1-3]。树干形状在测树学中是一个重要的调查因子,它既决定着树干材积的数量和质量,而且还是某些测树用表编制的核心问题。形数是树干实测材积与等底、同高的比较圆柱体体积之比,不仅是反映树干饱满程度的重要干形指标,也是计算立木材积及林分蓄积量的重要因子[4-6]。

早在19 世纪初,德国林学家在计算树干材积和确定其变化规律的同时,就创立了形数的理论[7]。此后有诸多研究者,如斯马林(1873)、 Girard J W(1933)、Maoss A(1939)、 苏联的丘林教授(1950)及我国的林昌庚教授(1961)等都提出了不同的干形指标和模型,从多方面对干形做了研究[8]。斯马林为克服胸高形数依树高生长出现的问题,根据研究结果大胆提出了正形数[9]；林昌庚[10-11]基于胸高形数易测和正形数的优点,根据林业工作中的经验,提出了“实验形数”；吴纪昌等[12]于1997年在形数研究中,提出了新绝对形数理论。在具体生产实践中,史团省等[13]对水杉(Metasequoiaglyptostroboides)幼林的形数和形率进行调查和测算,发现形数和形率变化随树高和胸径的增加而减小,为早期水杉幼林立木材积计算打下基础；岑巨延等[14]以广西速丰桉树(Eucalyptusrobusta)调查数据研究为基础,建立了桉树人工林二元胸高形数模型,对速丰桉林林木资源管理和生产有着重要作用；李崇武[15]分析速生桉树的实验形数,发现其最佳实验形数不是固定不变的,是随着区域、立地等因素的变化而变化。

本研究以湖南杉木(Cunninghamialanceolata)人工林为研究对象,研究胸高形数、实验形数在不同立地条件下变化的规律,以期为杉木人工林材积预测及经营数表编制等工作提供理论依据。

1 研究区概况

湖南省位于长江中游,地理坐标为北纬24°38′～30°08′,东经108°47′～114°15′,地处云贵高原向江南丘陵和南岭山脉向江汉平原过渡的地带,位于自西向东呈梯级降低的云贵高原东延部分和东南山丘转折线南端。其地貌类型多样,有半高山、低山、丘陵、岗地、盆地和平原。湖南为大陆性亚热带季风湿润气候,光、热、水资源丰富,各地年平均气温一般为16～19℃,日照时数1 238.7～1 868.7 h,年降水量1 200～1 800 mm,大部分地区海拔在100～800 m。湖南属亚热带常绿阔叶林区,主要自然生态系统类型为森林和湿地生态系统。用材树种主要有杉木、马尾松(Pinusmassoniana)、湿地松(Pinuselliottii)、杨树(Populussimonii)、檫木(Sassafrastzumu)、柏木(Cupressusfunebris)、樟树(Cinnamomumbodinieri)、楠木(Phoebezhennan)、榉树(Zelkovaserrata)和红豆杉(Taxuschinensis)等。地带性土壤以红黄壤和黄壤为主,零星分布有红壤、紫壤和黄棕壤。土壤质地以壤土和粘土为主,母质主要为板岩和页岩。林业用地面积1 299.8万hm2,活立木蓄积量5.05亿m3,森林覆盖率59.57%[16]。

杉木是湖南主要优良速生用材树种,其人工林面积和蓄积量占全省的33%和 41%[17],利用及栽培历史悠久。产杉区人民在长期生产实践中,遵循自然规律和经济规律,创造出以耕代抚、混农作业、稀植皆伐为特色的栽培制度及按湘、资、沅、澧四水流域为网络的杉木产、运、销系统,为现代产杉区的形成奠定了基础。

2 材料与方法

2.1 数据来源

数据来源于湖南省常德、郴州、衡阳、永州、邵阳、湘西州、益阳等7个地区的467株杉木标准木,各标准木所在的地区和立地条件各不相同,数据分布情况如表1所示。

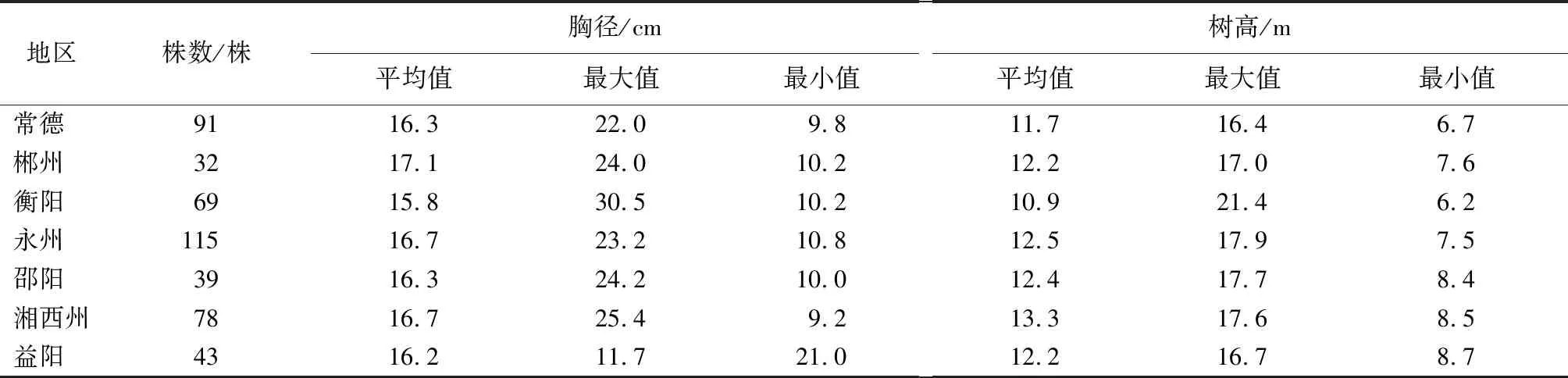
表1 样木基本情况表Tab.1 Basic information of sample trees

2.2 标准木形数计算

1) 胸高形数的计算。

以胸高断面为比较圆柱体的横断面的形数称为胸高形数,以f1.3表示,其表达式为:

(1)

式中:V为树干的实测材积；h为树高；d1.3为胸径。

2) 实验形数的计算。

实验形数的比较圆柱体的横断面为胸高断面,其高度为树高(h)加3m,记为f,根据其定义得到表达式为:

f

(2)

式中:V为树干的实测材积；h为树高；d1.3为胸径。

经(1)式、(2)式计算,467株杉木的胸高形数、实验形数如表2所示。

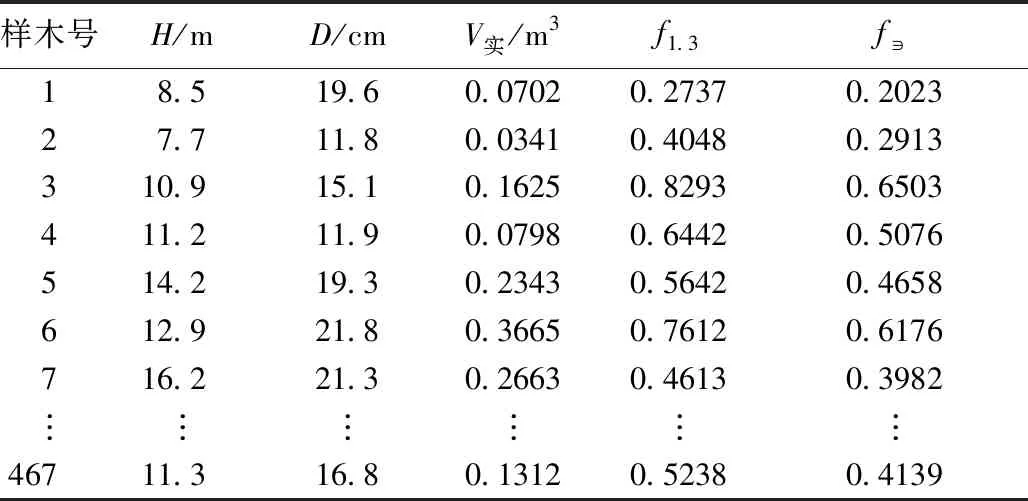
表2 杉木胸高形数及实验形数Tab.2 Breast-height form factor and experimental form factor of Cunninghamia lanceolata

2.3 分析方法

1) 变异系数法。采用变异系数法来比较湖南省杉木人工林胸高形数和实验形数的变异程度及稳定性。

2) 单因素方差分析。采用单因素方差分析法,研究胸高形数和实验形数在不同胸径级和树高级间是否具有显著性差异。

3) 相关性分析。采用person相关性分析,研究在不同的环境因子和林分因子下,杉木人工林胸高形数和实验形数是否具有显著性差异。

4) 回归分析法。由于形数的变化会受到各个环境因子和林分因子的共同作用,因此,在相关性分析的基础上,以各影响因子为自变量,以胸高形数和实验形数值为因变量,采用多元线性回归分析法,筛选出影响形数变化的显著因子,并建立自变量与因变量的多元回归方程。

3 结果与分析

3.1 杉木形数的稳定性分析

采用变异系数法,分别计算胸高形数和实验形数的变异程度,比较胸高形数和实验形数的稳定性,具体情况如表3所示。

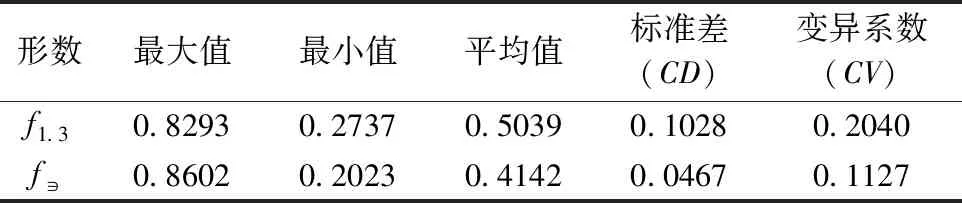
表3 形数的变异系数比较Tab.3 Variation coefficient comparison of form factor

由表3可知,实验形数的变异系数(0.112 7)小于胸高形数的变异系数(0.204 0)。因此,湖南杉木人工林单木的实验形数的稳定性比胸高形数好,这与诸多学者的研究结果相同,其普遍认为林木的实验形数稳定性要比胸高形数好。

3.2 杉木形数的变化规律分析

将胸径、树高划分等级组,以实验形数、胸高形数做为因变量,树高组与胸径组为因子组。由于杉木解析木的形数值为连续数值型变量,并且经检验,各树高组与胸径组之间的形数值服从正态分布。因此,本文采用单因素方差分析法,比较不同树高组和胸径组之间的形数均值差异。

1) 杉木形数随胸径的变化规律。

以胸高形数、实验形数为因变量,胸径为自变量,运用SPSS 26.0统计软件,采用单因素方差分析法,分析胸高形数和实验形数是否随胸径的变化而具有显著性差异,结果如表4所示。

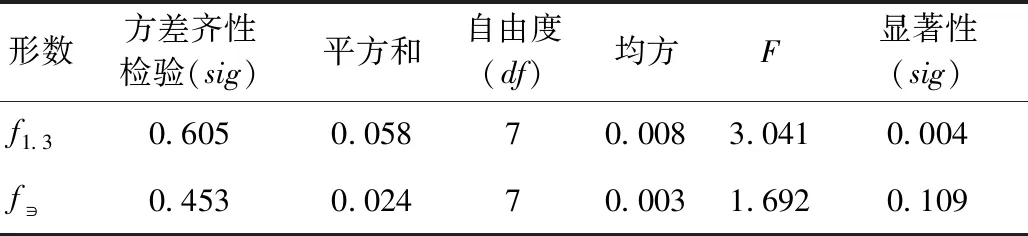
表4 形数与胸径方差分析表Tab.4 Variance analysis of form factor and diameter at breast height

当方差齐性检验值大于0.05(sig>0.05)时,表示单因素方差分析具有统计学意义。显然,本文采用单因素方差分析法来研究形数随胸径的变化具有可靠性。表4表明,当显著性小于0.05时(sig<0.05),说明不同胸径组的形数平均值存在明显的差异,即形数随胸径的变化而变化。从表4、图1中可以得到在胸径不同时,杉木人工林单木的胸高形数具有显著性差异,并且随着胸径的增大而减小,二者呈线性关系。实验形数随着胸径的变化无显著性差异。

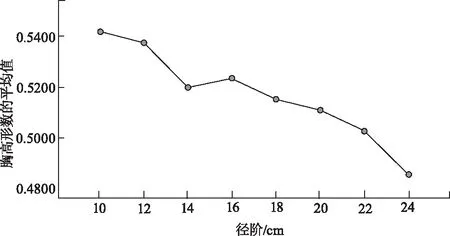
图1 胸高形数与胸径变化关系图Fig.1 Relationship between breast-height form factor and diameter at breast height

2) 杉木形数随树高的变化规律。

同理,运用SPSS 26.0进行形数和树高之间变化关系的方差分析,结果如表5所示。由表5可知:胸高形数的显著性大于0.05(sig>0.05),即胸高形数随着树高的变化无显著性差异；实验形数的显著性小于0.05(sig<0.05),故随着树高的变化,不同树高级间的实验形数均值具有显著性差异。说明实验形数随着树高的变化而变化。

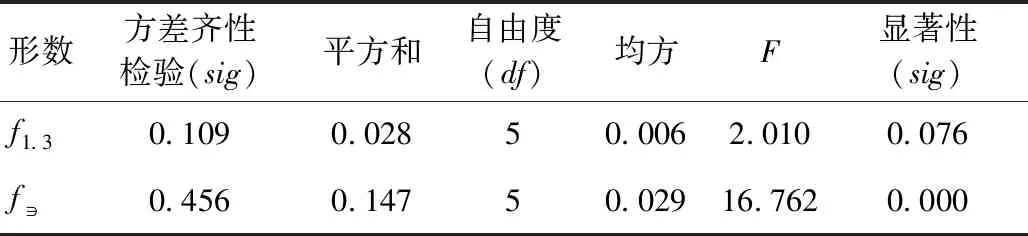
表5 形数与树高方差分析表Tab.5 Variance analysis of form factor and tree height

由图2可以看出,实验形数的值随着树高的增大而呈上升趋势,到达一定高度时,实验形数达到最高值,随后依树高的增大而呈下降趋势。

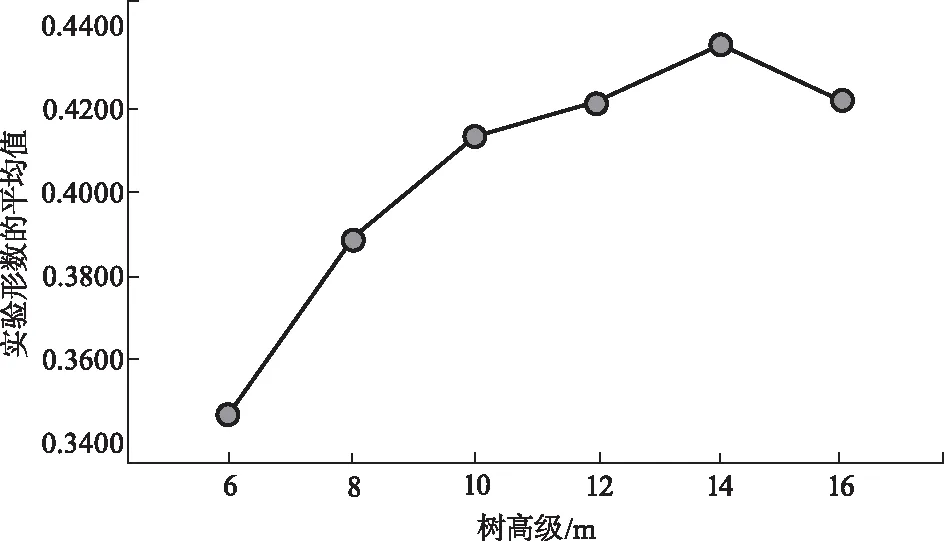
图2 实验形数与树高变化关系图Fig.2 Relationship between experimental form factor and tree height

3.3 杉木形数的影响因子分析

采用person相关性分析,分别以海拔、坡位、坡度、坡向、坡形、土壤类型、土壤厚度、石砾含量、干湿度、有机质含量等立地因子和树高(H)、胸径(D)、林分年龄、林分密度等林分因子为自变量,以求得的467株湖南杉木人工林解析木胸高形数和实验形数为因变量,分析不同环境因子及林分因子对胸高形数、实验形数的影响显著性及相关关系,结果如表6所示。

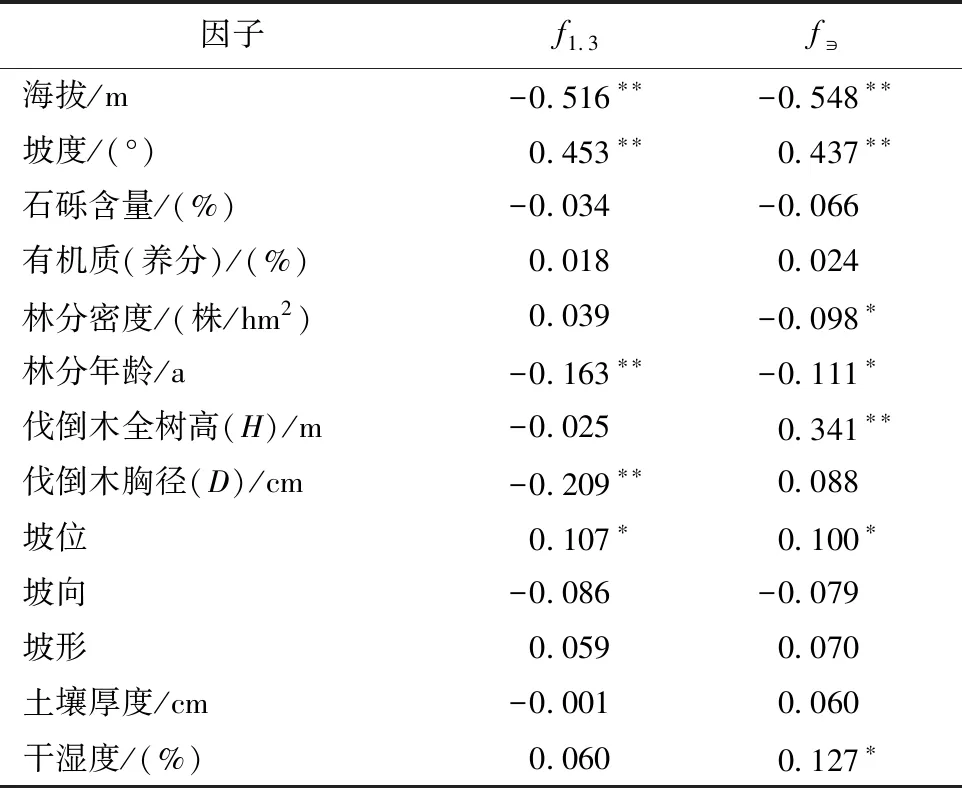
表6 影响因子的相关系数表Tab.6 The correlation coefficient of influencing factors

表6结果显示,胸高形数和实验形数的影响因子存在一定的差异:胸高形数与坡度呈极显著正相关(p<0.01),与坡位呈显著正相关(p<0.05),与海拔、林分年龄和胸径(D)呈极显著负相关(p<0.01),其余各因子对胸高形数无显著性影响；实验形数与海拔呈极显著负相关(p<0.01),与林分密度和林分年龄呈显著负相关(p<0.05),与坡度和树高(H)呈极显著正相关(p<0.01),并与坡位、干湿度呈显著正相关(p<0.05),其余各因子无显著性影响。

3.4 多元线性回归分析

由于形数的变化会受到各个立地因子和林分因子的共同作用。因此,在相关性分析的基础上,以各影响因子为自变量,以胸高形数和实验形数值为因变量,采用多元线性回归分析法筛选出系数显著的影响因子,并建立自变量与因变量的多元回归方程,结果如表7、表8所示。

由表7、表8的结果可知:两种形数模型的拟合效果均显著(sig<0.05),且膨胀因子均小于5(VIF<5),表明模型中各变量间不存在共线性,因此,模型的拟合效果具有统计学意义。结合表中各因子系数计算结果:

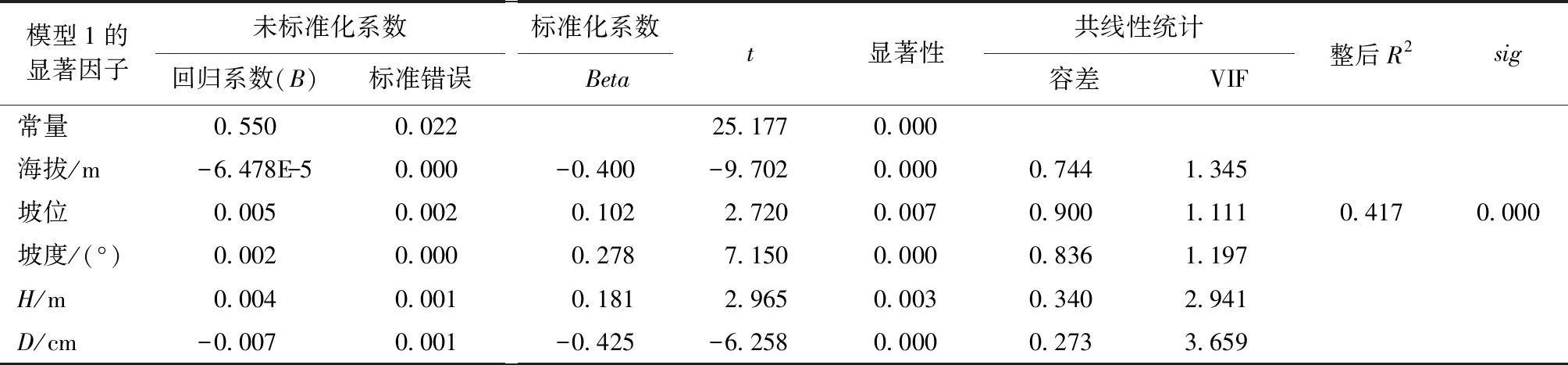
表7 胸高形数回归分析结果表Tab.7 The regression analysis results of breast-height form factor

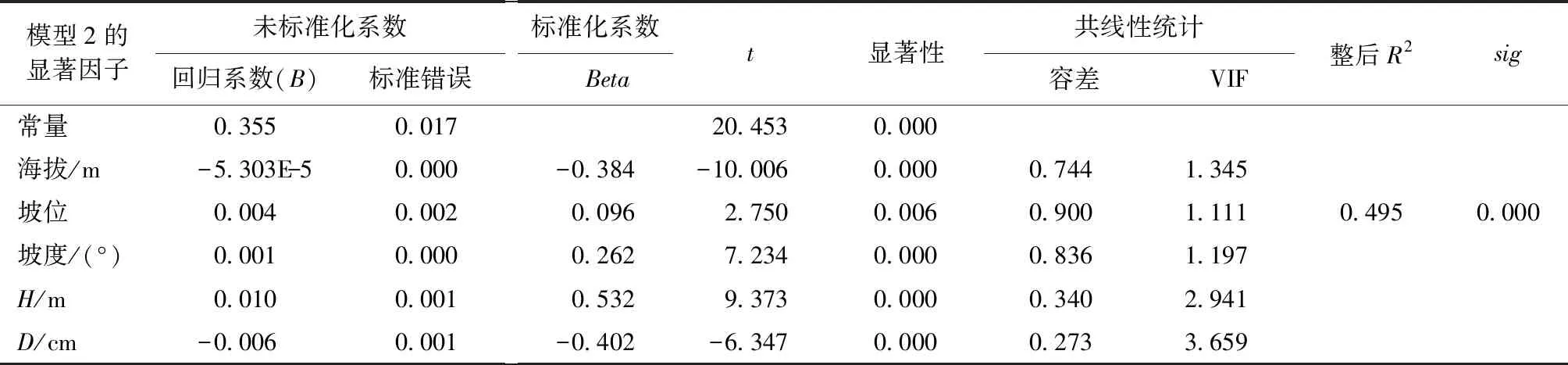
表8 实验形数回归分析结果表Tab.8 The regression analysis results of experimental form factor

1)杉木胸高形数综合预测模形为(模型1):

f1.3=0.550-6.478×10-5×HB+0.005×PW+

0.002×PD+0.004×H-0.007×D

2)杉木实验形数综合预测模型为(模型2):

f=0.355-5.303×10-5×HB+0.004×PW+0.001×PD+0.01×H-0.006×D

模型1、模型2中:“HB”表示海拔；“PW”表示坡位；“PD”表示坡度。

模型1调整后的R2为0.417,模型2调整后的R2为0.495,即回归方程可解释各自变异的41.7%和49.5%。模型1与模型2的系数显著因子均为海拔、坡位、坡度、树高(H)以及胸径(D),表明了这5个因子对湖南杉木人工林单木形数的差异具有显著影响,且变量间呈线性关系。

为进一步检验模型的精度,分别建立各模型的残差关系图,结果如图3、图4所示。

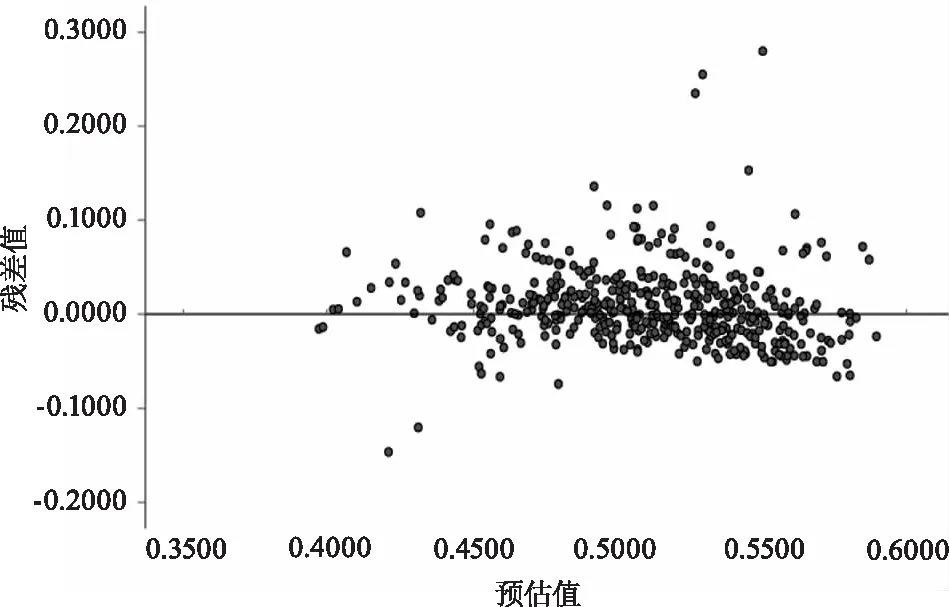
图3 模型1残差分布Fig.3 Residuals distribution of model 1

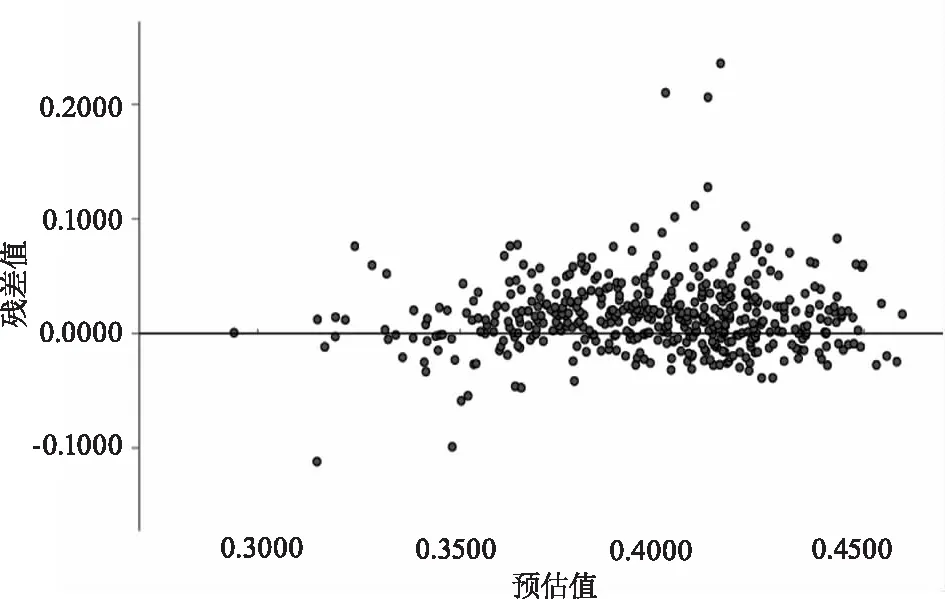
图4 模型2残差分布Fig.4 Residuals distribution of model 2

由图3、图4可知:两模型的残差值比较均匀地分布于横轴两侧,且两侧残差距横轴距离大致相等,仅有个别点远离横轴,残差近似服从正态分布。表明回归模型的预测精度较高。

4 结论与讨论

1) 采用变异系数法分析了实验形数和胸高形数的稳定性,其结果表明实验形数的稳定性要优于胸高形数。

2) 单因素方差分析法计算结果表明,胸高形数随胸径(D)的变化具有显著性差异(sig<0.05),会随着胸径(D)的增大而逐渐减小；实验形数随树高(H)的变化具有显著性差异(sig<0.05),并且在一定范围内随着树高的增大而增大。

3) Pearson相关性分析结果表明,胸高形数和实验形数的影响因子存在一定的差异。胸高形数与坡度呈极显著正相关(p<0.01),与坡位呈显著正相关(p<0.05),与海拔、林分年龄和胸径(D)呈极显著负相关(p<0.01);实验形数与海拔呈极显著负相关(p<0.01),与林分密度和林分年龄呈显著负相关(p<0.05),与坡度和树高(H)呈极显著正相关(p<0.01),并与坡位、干湿度呈显著正相关(p<0.05)。

4) 通过多元线性回归分析得到胸高形数回归模型与实验形数回归模型,系数达到显著水平的因子有海拔、坡位、坡度、树高(H)、胸径(D),这也表明了海拔、坡位、坡度、树高(H)、胸径(D)与杉木的形数具有显著的线性关系。结合表中各因子的系数计算结果,得到了杉木形数的综合预测模型:

f1.3=0.550-6.478×10-5×HB+0.005×PW+

0.002×PD+0.004×H-0.007×D

f=0.355-5.303×10-5×HB+0.004×PW+

0.001×PD+0.01×H-0.006×D

形数是表现树木干形的一个重要指标,形数作为立木材积三要素,对求算单木材积具有重要的意义[18-20]。本研究分析了杉木干形的特征及其影响因子,并建立了形数综合预测模型,研究结果对利用形数法来求算湖南杉木人工林单株材积或林分蓄积具有一定的指导意义。但由于数据有限,仅研究了部分立地因子和林分因子对于杉木干形的影响,在数据充足的条件下,进一步探究影响杉木干形的综合因素,可更好地为培育优质大径材提供理论依据。