基于平均故障间隔里程的汽车测试性分配方法

刘保国， 高 锦， 刘 振

（陕西重型汽车有限公司， 陕西 西安 710200）

近年来，随着汽车电控技术的发展，汽车装备使用的电子设备越来越多，系统变得越来越复杂，对测试性的要求陡增，使得测试性对汽车装备设计的影响也越来越大。测试性指标作为汽车测试性设计、测试性评估的量化参数，通常在汽车装备方案的论证阶段和初步设计阶段，由研制任务书提出。但由于研制任务书往往提出的仅为顶层的测试性指标要求，要实现该要求，则在汽车装备的研制过程中就需要将顶层的测试性指标，按装备层次，自上而下逐级分配给车辆的各个组成部分，以明确车辆各组成部分的测试性定量要求，以此作为汽车装备组成分系统测试性设计的依据。而国内对于重型汽车装备测试性设计的研究尚处于起步阶段，还没有针对重型汽车装备测试性指标的分配方法。本文以某重型越野汽车装备测试性指标分配为例，介绍一种基于平均故障间隔里程（Mean Miles Between Failures，以下简称“MMBF”）的汽车装备测试性指标分配方法。

1 测试性指标

测试性指标作为测试性定量要求的量化表示形式。根据GJB2547A的规定，结合工程应用实际，测试性指标一般包括故障检测率、故障隔离率和虚警率。其中故障检测率是指用规定的方法正确检测到的故障数与故障总数之百分比；故障隔离率是指用规定的方法将检测到的故障正确隔离到不大于规定模糊度的故障数与检测到的故障数之百分比；虚警率是指在规定期间内发生的虚警数与同一期间内故障指示总数之百分比。

根据某重型越野汽车研制任务书，该装备的测试性指标为：故障检测率≥96%；故障隔离率≥93%；虚警率≤5%。

2 测试性指标分配的数学模型

测试性指标分配的数学模型可用于把顶层的测试性指标分配给系统级以下各个层次，以便进行产品的测试性设计。以故障检测率 （FDR）、故障隔离率 （FIR） 和虚警率（FAR） 作为汽车装备的测试性指标。根据测试性指标的定义，FDR的基本数学模型可表示为：

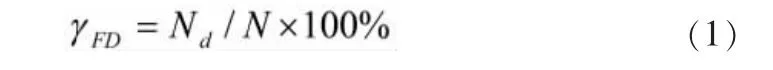
式中：Nd——检测到的系统故障数；N——系统发生的故障总数。

FIR的基本数学模型可表示为：

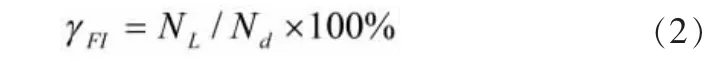
式中：NL——用规定的方法正确隔离到可更换单元的故障数。

FAR的基本数学模型可表示为：

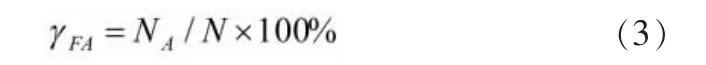
式中：NA——规定期间内发生的虚警数。

式（1）、（2）、（3）适用于做测试性验证统计，在做测试性定量指标分配时并不适用。由于汽车系统的每一子系统对车辆的测试性都会产生影响，这种影响一般在车辆中没有其他单元可以替代。因此，汽车系统的测试性由组成子系统的测试性综合而成。本文定义故障率为在规定运行里程内，车辆在单位运行里程内发生的故障数。组成分系统的各子系统（或单元） 的故障率求和即为分系统故障率：

式中：λk——第k个分系统的故障率；λi——第i个组成子系统的故障率。

根据故障检测率的概念，改写式（1）：

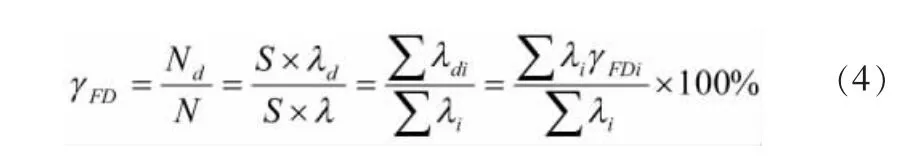
式中：γFD——系统故障检测率；γFDi——第i个组成子系统的故障检测率；λi——第i个组成子系统的故障率；λdi——第i个组成子系统可检测的故障率；S——车辆的运行总里程。

设γFDsr表示待分配的系统故障检测率，γFDk表示第k个子系统或组成单元的故障检测率分配额，n为装备分系统或组成单元个数，代入式（4），可求得FDR的分配数学模型为：

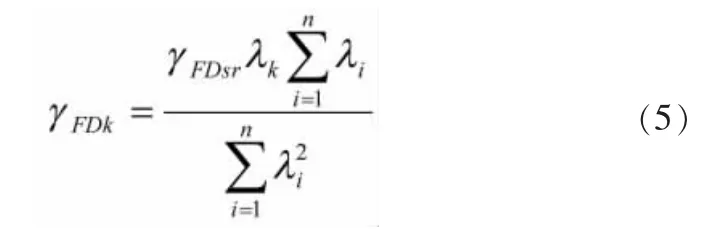
同理，改写式（2）

式中：γFI——系统故障隔离率；γFIi——第i个组成子系统的故障隔离率。

设γFDsr表示待分配的系统故障检测率；γFIKi表示第k个子系统或组成单元的故障检测率分配额；n为装备分系统或组成单元个数，代入式（5），可求得FIR的分配数学模型为：

借鉴其他装备领域的虚警率分配经验，通常将订购方对装备的虚警率指标直接作为各组成部分虚警率指标要求。于是FAR的分配数学模型可表示为：

式中：γFAk——第k个组成子系统的虚警率；γFAsr——待分配系统的虚警率。

3 基于MMBF的测试性指标分配

基于MMBF的测试性指标分配方法是从确保车辆的可用度方面考虑，先根据MMBF计算系统的故障率，然后采用专家评分法对系统故障率进行分配，按照在组成系统的各部件中，故障率高的部件应分配较高的自动故障检测率和故障隔离率原则对车辆的测试性指标进行分配。下面以某重型越野汽车测试性指标分配为例，介绍该方法的应用。

在某型号重型越野汽车测试性指标的分配中，直接将车辆的不大于5%的虚警率指标作为各组成部分的指标要求。对于故障检测率和故障隔离率的分配，则采用基于MMBF的测试性指标分配方法进行分配。最后，通过测试性分配指标验证试验，验证车辆的测试性设计水平是否达到了测试性分配指标要求。根据测试性分配指标验证结果，对测试性分配方法的合理性、有效性进行评价。

3.1 故障率分配

根据某重型越野汽车研制任务书，该装备的基地试验平均故障间隔里程应不小于1200km，于是其平均故障率可计算为：

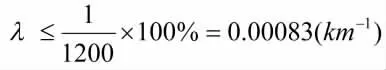
采用综合评分法对系统故障率进行分配，按组成子系统技术水平、复杂程度、重要程度、工作时间以及环境条件5种因素对子系统进行评分，然后根据子系统评分系数分配故障率。其中的评分原则如下。

1） 技术水平：根据子系统目前的技术水平和成熟程度评定。水平最低、最不成熟的评10分，水平最高、最成熟的评1分。

2） 复杂程度：根据子系统的零部件数量以及它们组装的难易程度评定。最复杂的评10分，最简单的评1分。

3） 重要程度：根据子系统在整车中的重要程度评定。最不重要的评10分，最重要的评1分。

4） 工作时间：根据子系统工作时间评定。工作时间最长的评10分，最短的评1分。

5） 环境条件：根据子系统所处的环境评定，最恶劣严酷的环境条件评10分，环境条件最好的评1分。

子系统评分数：

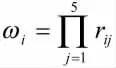
式中：ωi——第i个子系统的评分数；γij——第i个子系统，第j个因素的评分数；j=1代表技术水平；j=2代表复杂程度；j=3代表子系统重要程度；j=4代表工作时间；j=5代表环境条件。

系统总评分数：

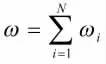
式中：ω——系统总评分数；ωi——第i个子系统评分数。

子系统评分系数：

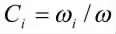
式中：Ci——第i个子系统评分系数。

于是分配给各子系统的故障率：

式中：λi——分配给各子系统的故障率；λs——系统规定的故障率指标。

某重型越野汽车组成子系统评分及故障率分配结果见表1。

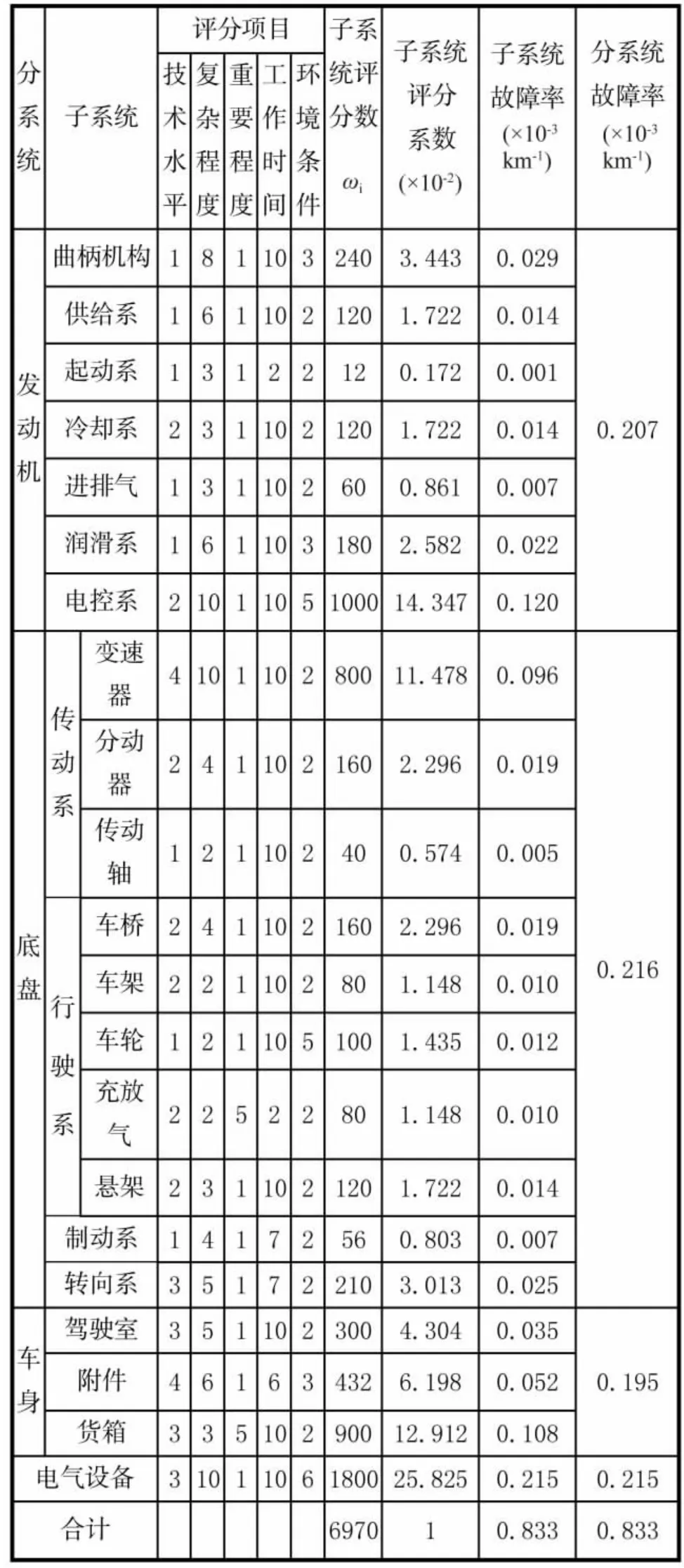
表1 各子系统评分及故障率

3.2 测试性指标分配

按照先计算后修正与验算的步骤进行测试性指标的分配。根据式（6）、（7）计算各组成部分故障检测率、故障隔离率分配值。若计算的分配额故障检测率γFDk≥1，或故障隔离率γFIk≥1时，应将γFDk和γFIk修正为大于待分配系统相应指标值而小于1；若γFDk≤γFDsr，或γFIk≤γFIsr时，适当提高相应分配指标值；对于要求平均故障修复时间小的单元，或故障影响大的单元，适当提高其检测率分配额。指标值修正后，利用式（4）、（6）验算分配指标值，使分配的故障检测率满足：

故障隔离率满足：

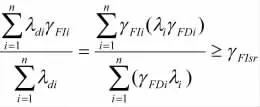
通过计算、修正和验算，获得某型号重型越野汽车故障检测率、故障隔离率初步分配计算值、修正值、验算值，见表2。修正值作为该重型越野汽车测试性指标分配值。

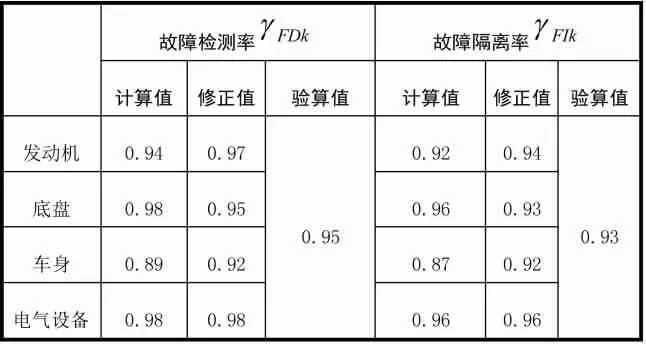
表2 测试性指标分配工作单

3.3 测试性验证试验

测试性验证试验的方法分为故障注入试验方法和自然故障统计方法两大类。自然故障统计方法是直接统计产品在使用过程中自然发生的故障和其故障检测与隔离信息，据此评估产品的测试性水平是否满足分配的测试性指标要求。故障注入试验方法是在研制的产品试验样机中注入一定数量的故障模式，用测试性设计规定的或其他辅助的测试方法进行故障检测与隔离，按其结果估计产品的测试性水平并判断是否达到了分配的测试性指标要求，决定接收或拒收。

某重型越野汽车的测试性经过基于MMBF的测试性指标分配方法对该装备的测试性指标进行分配，完成分系统或子系统的测试性设计，经过测试性试验验证，试验结果见表3。

表3 测试性试验结果

该重型越野汽车测试性试验验证结果表明，采用基于MMBF的测试性分配方法对车辆的测试性进行分配是合理、有效的。

4 结论

采用基于MMBF的测试性指标分配方法对汽车装备的测试性指标进行分配，先根据MMBF计算系统的平均故障率，然后采用专家评分法对系统的平均故障率进行分配，按照在组成系统的各部件中，故障率高的部件应分配较高的自动故障检测率和故障隔离率原则对汽车装备的测试性指标进行分配。最后，通过某重型越野汽车测试性验证试验，采用MMBF的测试性指标分配方法能有效对汽车装备的测试性指标进行合理分配，有利于减少车辆的维修时间，提高车辆装备的可用性。该方法对汽车装备的测试性设计人员有一定的参考价值。