基于简化超球体SRUKF的FOG和SS组合定姿算法
2020-11-26聂高胜朱高兴
聂高胜,朱高兴
(江西师范高等专科学校 物联网学院,江西 鹰潭 335000)
0 引 言
卫星一般采用光纤陀螺实现定姿。光纤陀螺是一种基于Sagnac效应的角速度传感器,与传统的机械陀螺相比具有重量轻、体积小、动态范围大、实时性好以及抗干扰能力强等优点,但存在解算姿态误差随时间积累的缺陷。星敏感器是一种通过测量恒星而实现定姿的天文传感仪器,具有测量精度高、不受外界干扰等优点,但实时性较差。两者组合到一起定姿,可优势互补,形成一种长航时卫星定姿方式[1]。
光纤陀螺与星敏感器的信息融合一般采用卡尔曼滤波算法。卡尔曼滤波较适用于线性系统,对非线性系统的处理效果较差,但现实中的系统基本都是非线性系统。文献[2]将简化无迹卡尔曼滤波(Simple Unscented Kalman Filter,SUKF)应用到惯导系统的非线性初始对准,取得了很好的效果;文献[3-4]分别将SUKF应用到惯导与GPS和惯导与地磁的非线性组合导航中,实现了更高精度的定位定向。本文则首次将SUKF算法应用到光纤陀螺与星敏感器的组合定姿中,通过建立简化组合系统模型,采用反馈陀螺漂移误差校正姿态的方式,实现了更高精度的光纤陀螺和星敏感器组合定姿。
1 姿态解算算法原理
光纤陀螺和星敏感器组合算法原理如图1所示。其中:φFOG、θFOG、γFOG为三轴光纤陀螺系统解算得到的三维姿态;φSS、θSS、γSS为星敏感器解算得到的三维姿态;εX、εY、εZ为滤波过程中估算的三维陀螺误差。光纤陀螺系统输出三维惯性姿态信息,星敏感器输出三维星敏姿态信息,利用简化的SUKF算法,将两者姿态角信息之差作为观测量进行最优滤波,并用滤波过程中估算的陀螺误差修正惯导输出,从而提高组合系统的姿态解算精度。
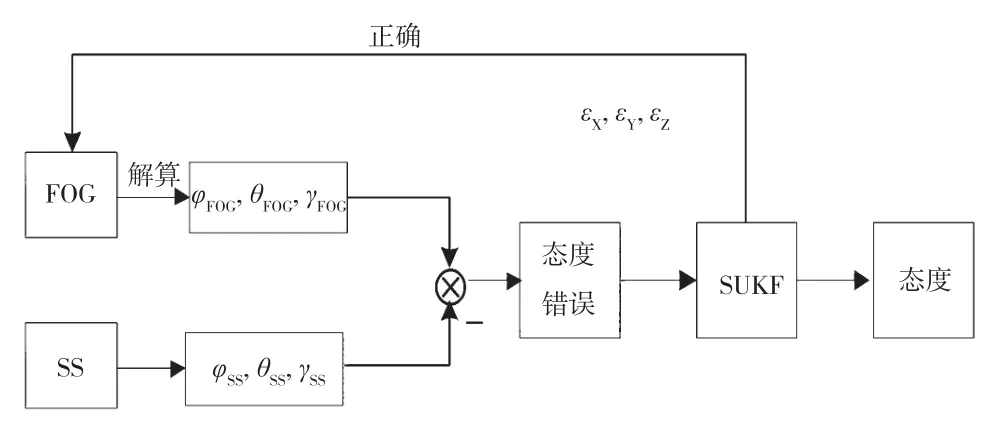
图1 光纤陀螺和星敏感器组合定姿算法原理框图
2 光纤陀螺和星敏感器组合系统模型建立
2.1 状态模型
选择东北天地理坐标系(E、N、U)为导航坐标系,建立卡尔曼滤波的状态方程为:
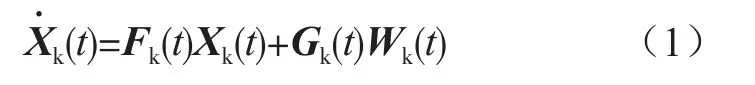
式(1)中,组合导航系统的状态量为:
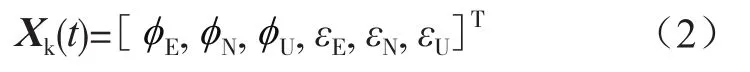
式中,φE、φN、φU为三维姿态误差角,εE、εN、εU为三维陀螺常值漂移。
系统的状态转移矩阵Fk(t)为:

式(3)中,FN中的元素与惯导系统的误差方程相对应,Cbn为捷联姿态矩阵。
系统的噪声转移矩阵为:
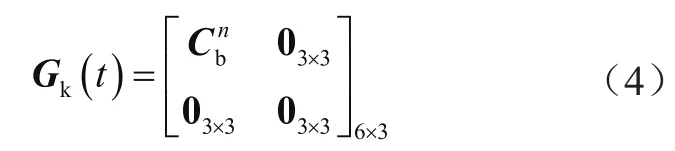
系统噪声矢量为:
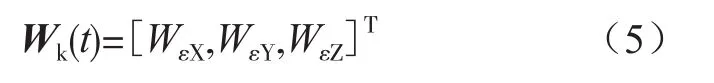
2.2 量测模型
根据量测信息建立的量测方程为:
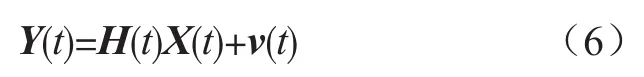
其中,Y(t)=[φx,φy,φz]T,量测矩阵为H(t)=[I3×303×3],v(t)为量测噪声矩阵。
3 SUKF滤波算法简介
无迹卡尔曼滤波是一种非线性滤波方法。对于非线性系统,它的滤波性能优于卡尔曼滤波。
假设一个维数为n的离散化非线性系统方程和量测方程为:
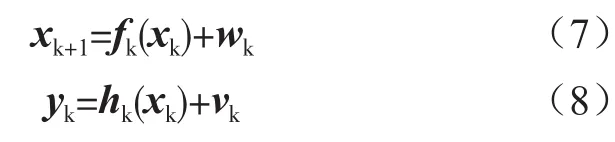
其中,xk为系统的状态向量矩阵,fk为状态变量的传播函数,wk为系统的噪声向量,yk为量测向量,hk为量测向量矩阵,vk为系统量测噪声向量。
SUKF滤波的本质是通过在的附近构造一组Sigma采样点,并计算Sigma采样点,估计出状态一步预测和一步预测均方差,从而进行滤波,具体算法过程描述如下。
首先,设定滤波的初始值,即:


其次,计算Sigma采样点。此时,根据i的取值,分3种情况进行讨论。
(1)当i=0时,有
(2)当i=1,2,…,n时,有
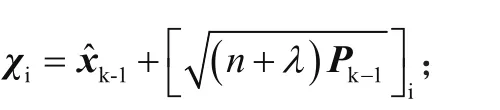
(3)当i=n+1,…,2n时,有
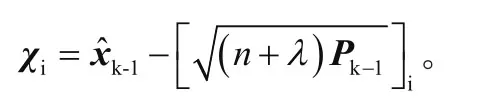
其中,λ=α2(n+k)-n为标量。α是很小的正数,可取10-4≤α≤1,k通常设置为零。
再次,通过时间更新方程更新时间信息,具体为:
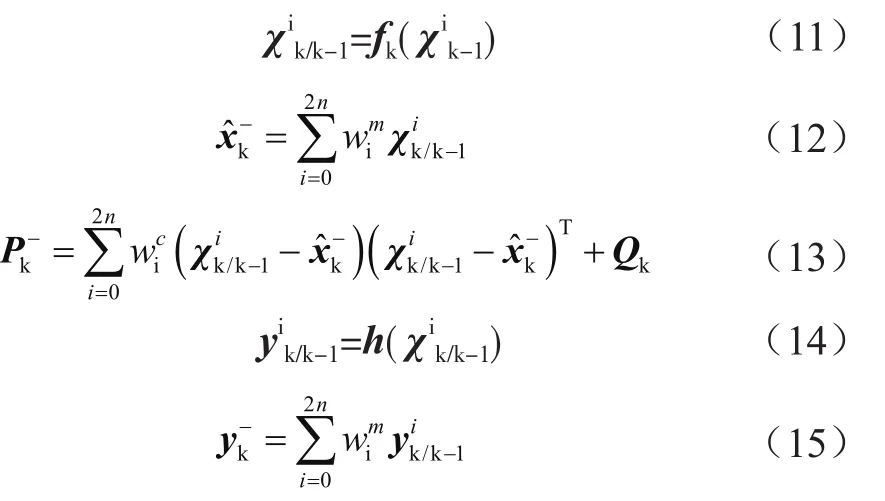
最后,量测更新方程为:
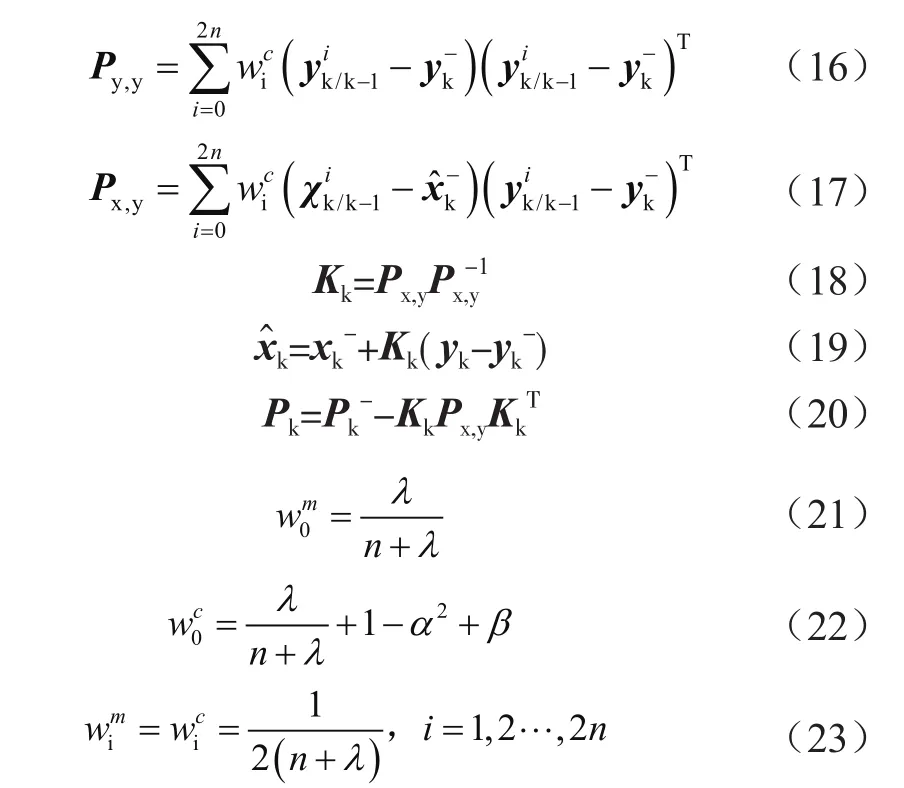
其中,β的取值与x的分布有关,通常高斯分布的x取值为2。
4 仿真试验验证
试验选用三轴的光纤陀螺产品,陀螺常值漂移为0.05°/h(1σ),是衡量陀螺性能的关键指标。陀螺置于带有北向基准的测试平台上,通电稳定后采集三向陀螺3 600 s静态输出原始数据;星敏感器的量测精度设为1'',计算机仿真生成导航坐标系下3 600 s静态的三向姿态数据用作星敏感器的静态导航输出数据。分别用纯FOG、卡尔曼滤波(KF)和简化SUKF滤波算法进行离线仿真计算,并对比分析解算结果。3种解算方法的姿态解算结果对比如图2所示。可以看出,简化SUKF滤波算法解算的三向姿态角误差明显小于其他两种方法。
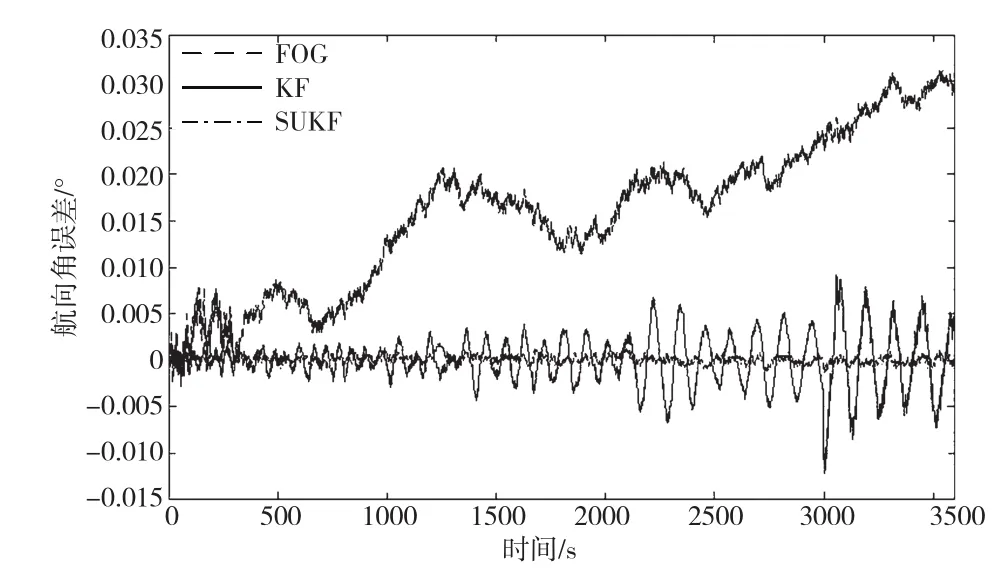
图2 3种算法解算的航向角误差对比
由于3种算法的组合导航误差曲线都比较平滑,可以用姿态的最大误差和标准差来评价其精度水平。表1列出了3种算法的统计结果,其中航向角、俯仰角以及横滚角是衡量姿态的3个重要指标。
由仿真结果可见,在相同的3 600 s导航时间内,简化SUKF算法解算的三向姿态最大误差约是KF算法的20%,约是纯FOG算法的5%,SUKF算法解算的三向姿态标准差约是KF算法的16%,约是纯FOG算法的6%。可见,相比纯FOG和KF算法,简化SUKF算法可得到更高精度的姿态角。因导航误差有随机性和随时间发散性,最大误差和标准差都是指3 600 s内时间段内所有数据对于同一方法同一指标的结果。比如,SUKF方法“head”在3 600 s这个时间段的导航误差最大误差值是6.639,这段时间导航的标椎差是1.602。
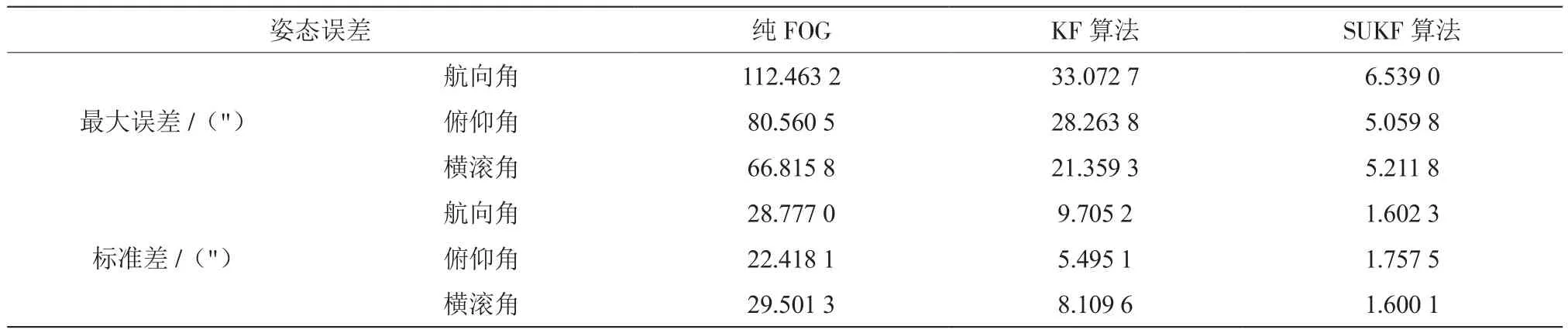
表1 3种算法解算的姿态误差统计
5 结 论
仿真试验结果表明,将SUKF滤波算法应用到光纤陀螺和星敏感器的组合定姿中,可很好地处理非线性系统,且在长航时比卡尔曼滤波和纯FOG解算的姿态角精度更高,证明了SUKF滤波算法的正确性和可行性,可为其今后在卫星定姿中的进一步应用提供理论参考。
