考虑系统延时的微电网有功功率分布式控制策略

王 涛

（国电南瑞科技股份有限公司，江苏 南京 211106）

0 引 言

根据目前的实际情况来看，电力系统中新能源应用占比迅速增长。其中，太阳能和风能为两种非常重要的表现形式，但是存在一定的波动性和随机性，无法全方位满足电网系统运行需求。微电网的出现可以满足分布类电源的基本需求，还能在中低等级的电压下连接分布设备。微电网具有变化多样、容量小以及节点多等特点，使得旋转主机和电网控制出现了不同的效果。在考虑微电网特点的情况下，电网使用集中控制方案时对中央控制设备有一定的要求。不仅需要成熟的技术，还需大量的计算数据。分布控制方案使用了大量控制设备，完成了系统协同控制，是微电网未来的主要发展方向。一致性算法属于一种特点明显的控制计算方式，利用疏通信号网络的方式完成节点一致性控制。目前，一致性算法已经在微电网中得到了广泛应用。使用这种算法时，一定要进行经济调控和二次控制，可借鉴频率电压调控的研究成果。

分布式控制策略和系统运行之间具有直接关系。延时性是微电网运行过程中出现的主要影响因素。在考虑不同的通信延时阶段的情况下，需要研究多种系统的稳定条件，设计具有离散型和一致性的微电网控制方案，合理分析延时性对控制方案造成的实际影响。另外，需要建立微电网分布小型基站模型，逐渐减少延时性造成的影响。本文在综合国内外已有研究的基础上进行了系统延时性研究，其中主要包括节点控制性和系统延时性，并合理分析了在系统延时状态下的微电网功率分布和性能状态，能够提供稳定的控制依据。此外，在综合各方面条件的情况下提出了适应性分布控制方案，并使用多个场景验证了仿真效果。

1 基于一致性的微电网有功功率控制

1.1 图论与一致性控制

在进行分布式控制工作中，为了能够有效统计不同节点间的信息数据，可以采用交互成图的方法进行表示。本文以通信系统为例，分析G(V,E)的无向性。其中，V={v1,…,vn}代表网络中全部的n个节点，是网络中不可缺少的连接部分；E⊆V×V表示网络中的通信线路，{Vi,Vj}∈E表示i、j两者间的通信连接。在整个通信网络G中拓扑结构可以采用式（1）进行描述：

当所包含的对角元数值为0时，与之相对的非对角元数值便被定额在非负数区域。在这种情况下，aij大于0，证实节点i与j之间存在数据间的连接，否则aij的数值默认为0。

由于分布式控制系统具备一致性，所有节点彼此间都会对信息数据进行交互工作，以此确保所有节点处于相同状态，这种状态变量又被成为一致性变量，通常表示为：

式（2）中，xi(t)为节点i的一致性变量。就目前一致性算法而言，最经典的是以参考值xref代入少量节点来对所有节点数值进行约束，从而使其维持在参考值的范围内，即：

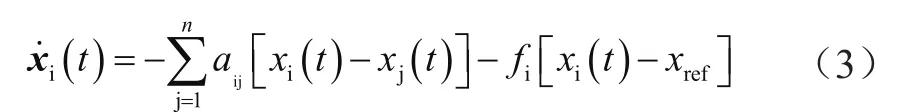
式中：aij表示邻接矩阵A中的元素；fi为节点i的牵制系数，代表i的参考值引入情况。

另外，拉普拉斯矩阵对定义网络有着十分重要的影响，通常情况下以L=(lij)n×n作为表现形式，都对其进行定义的只有邻接矩阵，具体情况为：

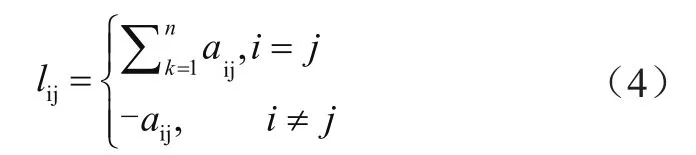
在进行牵制矩阵的选择过程中，可以选用矩阵F=diag(f1…fn)，矩阵1n=[1…1]T。因此，可将式（3）改写成为式（5）：

综上所述，当G为连通网络且所选矩阵F不等于0时，那么L+F能够满足0≤λ1≤…≤λn，则网络系统中的全部节点状态最终都能有效收敛到参考值xref。

1.2 微电网有功功率分布式控制架构

为了确保微电网总功率能够达到合理的平衡状态，需对微电网中涉及的各台DG（分步式电源）的有功功率进行调整，并合理分配容量比例，以实现对微电网的有效控制。

下垂控制策略和一致性控制策略是人们日常生活中最常用到的微电网有功分布控制手段。但是，下垂控制策略具有区域限制，只能在本地使用，作用是调节当地DG的有功功率，以确保DG输出的频率符合相关要求。

一致性控制策略则是利用当前最先进的计算机网络技术，在通信网络的内部空间中进行信息数据间的置换与交流，并以此为基础调整所有的DG有功功率。

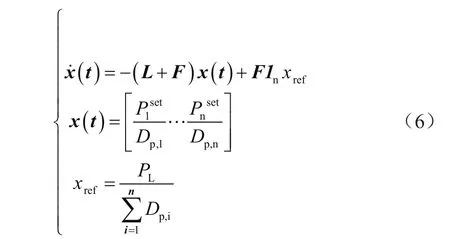
在不考虑微电网内部电路耗损的情况下，可以选用式（6）对有功功率进行控制调整。

2 微电网延时具体影响分析

2.1 分布控制模式中延时建模

微电网中延时性主要分为两种形式。第一种，不同节点之间存在的通信延时性。这种延时性主要受距离、通信结构以及方法等因素影响。第二种，时微电控制延时性。这种控制方法可以减少设备使用过程中的多种影响因素。微电网一致性控制程序中，在确定了控制设备和具体的通信网络后，需要将延时情况设为具体的常数。在两种延时情况都存在的背景下，传统微电网具体的分布控制方程为：

式中，tii表示DGi的控制延时，tij表示DGj信息传递到DGi所用的延时[2]。

2.2 分布控制过程中延时影响分析

若系统中出现了系统延时性，那么会直接影响系统稳定性。系统稳定和重要支点之间有着直接关系，为了确保系统稳定性，需要替换极点位置和复位面，并确定和替换使用的方程式[2]。

在受到延迟影响的情况下，一致性特征控制方程为：

式（8）中，di表示节点i的度，即拉普拉斯矩阵相对应的对角元素。通过分析得出，tii=0的状态下，扫描控制系统所有的极点都应该位于左半开面。这种状态下若出现了系统延时性，能及时应对半开极点问题，以满足At(s)=(aije-st11)n×n的需求，确保系统延时性存在于虚轴极点。这种情况下，需要找出对系统造成影响的限制条件，使系统不完全处于虚轴极点，才能使得系统时刻处于稳定运行状态[3]。

3 系统延时微电网控制方案

3.1 微电网功率分布控制策略设计方案

将式（7）进行改写，得出：

可以看出，在控制器中输入信号可以确定本地节点。造成系统运行不稳定的主要因素有xi(t)和ui1(t)，造成系统失稳的主要是ui1(t)，所以需要将其带入皮亚诺算式中确定具体的常数，以保障多项指标的稳定性和安全性[4]。使用时刻信息进行预测，若是取0＜ui2(t)＜1的状态下能得出本地程序的状态，同时能逐渐降低系统的延迟性。通过调整式（9），将其变成算式的标准形式，制定完善的微电网功率分布控制方案：

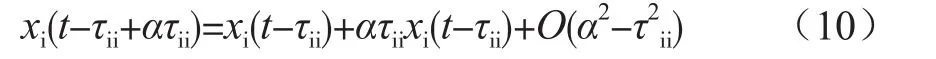
式（10）提供了一种使用时刻的信息对未来信息进行预测的方法。若取0＜a＜1，则可通过式（10）估计出t-(1-α)τii时的本地状态，等效地减小了系统的控制延时。

3.2 微电网有功功率分布式控制策略性能分析

通过对系统方程进行特征分析，得出：

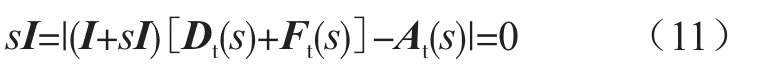
式中：P=diag(p1…pn)。

需要利用对角矩阵实施特征判断，找出存在的根本问题，还需要确保矩阵具有的适用性。若是在通信线路中出现了延时性过高的问题，为保障系统稳定运行，需逐渐完善矩阵结构。系统中需要严格要求所有矩阵使用方程措施进行结论确定，为系统日常维系提供良好环境和基础。在进行系统控制过程中，需要保障多种条件符合要求，验证算式具有的合理性和真实性，设置具体参数，完成最终赋值[5]。

通过分析式（11）可以得出，控制方案虽然可以保障系统稳定运行，但是所有条件必须满足需求。在A逐渐向0靠拢时，可以验证多个算式的相同性。一定要合理设置参数值，改变以往的控制方案，才能确保系统稳定运行。在A=0.5的情况下进行举例说明，代入式（11），可以得出延迟较小的临界值：

对于式（11）和式（10），若是在不同的通信环境中，需要根据实际情况选择控制方案，使系统可以承受最大的耐久度，增加80%左右的延时性，进而提升微电网的适应能力[6]。

4 仿真分析

为验证相关分析的正确性和所提策略的有效性。基于两个微电网算例进行仿真测试，分别对应有环的通信网络和无环的通信网络。算例1中DG1为牵制DG，算例2中DG5为牵制DG，分别如表1和表2所示[6]。

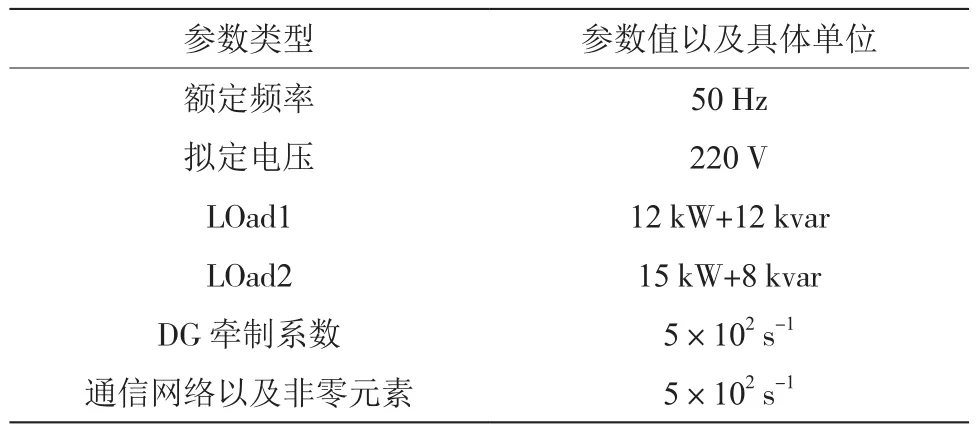
表1 算例参数

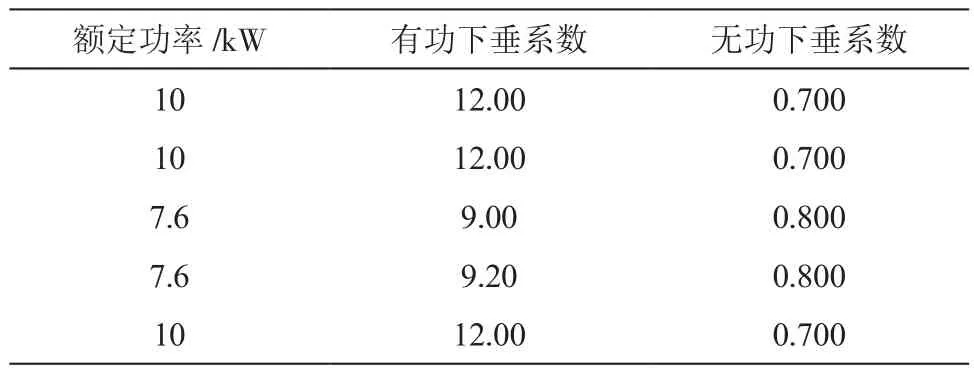
表2 DG额定功率和下垂系数

微电网中DG的控制时主要取决于控制器的采样和运算环节，一般在1 ms以内。不同节点之间的通信延时根据节点之间距离的不同，一般在几毫秒至几百毫秒之间。仿真中设定改进控制策略参数a=0.5，两种控制策略分别要求控制延时小于0.5 ms和0.9 ms。对于算例2，两种控制策略要求控制延时小于0.3 ms[7]。

5 结 论

本文针对微电网中通信控制和延迟性进行研究，提出了比较完善的功率分布控制方案。控制延时性会直接影响系统稳定性，还会逐渐改变收敛速度和性能指标。为了解决这种问题，提出了良好的控制计算方案，可为控制系统构建提供良好的环境。