基于动量LMS算法的变步长次级路径在线建模ANC系统
2020-11-25
(重庆邮电大学 光电工程学院,重庆400065)
随着经济的发展与城镇化的不断推进,城市交通噪声也日益增加。随之而来的是,居住在城市主干道周围的人们对美好居住环境的向往与日益增长的噪声之间的矛盾日趋严重。2018年《中国环境噪声污染防治报告》 的相关噪声检测数据显示,夜晚噪声未达到国家噪声标准的为79.8%,研究表明长期暴露在噪声环境中严重影响人们的身体健康。为了降低噪声对人们生活的影响,在日常生活中主要采取声屏障——被动噪声控制PNC(passive noise control)方法来消除噪声对人体的危害。被动降噪的方式对中高频的噪声降噪效果显著,然而,分析发现在城市道路两侧的居民主要受低频噪声的影响。
低频噪声比较理想的方式是采用主动噪声控制ANC(active noise control)系统,根据声音的叠加原理,产生与噪声源幅值相同、相位相反的声波来消除空间中噪声。针对低频噪声,通常采用主动噪声控制技术,在室内噪声ANC 控制系统设计中,次级路径建模的精度直接影响整个系统的降噪效果。在此,针对主动噪声技术中所涉及的次级路径建模的问题进行了研究,改进现有主动噪声控制算法,提出了次级路径变步长动量LMS算法对次级路径进行实时建模。
1 主动噪声控制系统原理
由于交通噪声主要以非周期的低频噪声信号为主,而宽带前馈型主动噪声控制系统对非周期低频噪声的控制具有较好效果,故在此选取宽带前馈型主动噪声控制系统,对室内交通噪声进行控制。
1.1 主动噪声控制系统基本原理
主动噪声控制是消除低频噪声行之有效的方法。使用主动噪声控制系统产生一个与原噪声信号幅值相等、相位相反的抗噪声信号,根据噪声源和抗噪声源相消干涉原理[1],降低指定区域噪声的声压级。
针对不同场景的噪声,主动噪声控制策略主要有2种:前馈控制和反馈控制。前馈控制是指使用传感器对噪声源进行测量,在噪声源的信号也就是初级声源的信号未到达次级声源之前,得到参考噪声信号。反馈控制与前馈控制相比,没有在次级声源前装传感器,在没有噪声输入的前提下进行噪声抵消。反馈型系统只能抵消窄带周期性的噪声,在此主要对前馈控制进行设计。主动噪声控制系统可以分为4种:宽带前馈型、窄带前馈型、反馈型和多通道型。
1.2 宽带前馈性ANC系统
宽带前馈型ANC系统[2]主要包含参考传感器、对消扬声器、误差传感器以及主动噪声控制器。宽带前馈单通道ANC系统通常以空气管道中的ANC系统为例,如图1所示。主动噪声控制器接收来自参考传声器接收的参考信号x(n)和误差传声器接收的误差信号e(n),经过自适应滤波算法的处理输出抗噪声信号y(n)。y(n)驱动次级扬声器发出次级声信号,两者相互干涉相消,使得待消声区域声压级降低。

图1 宽带前馈型主动噪声控制系统Fig.1 Broadband feedforward active noise control system
2 次级通道在线建模的方法
在实际应用中,由于室外环境变化造成次级路径的传递函数是时变的,次级路径建模的精确性直接影响整个系统的稳定性,因此针对次级路径的实时建模是保证主动噪声控制系统稳定性的关键。
2.1 现有结构
文献[3]使用附加高斯白噪声作为建模信号,对次级路径进行在线建模,Eriksson 的次级路径在线建模主动噪声控制系统如图2所示。由于建模信号与控制信号相互干扰,会导致系统发散,虽然解决了次级路径在线建模的问题,但降低了系统稳定性。后续又提出了多种方法以改进Eriksson 的结构提高系统的性能。

图2 Eriksson 的次级路径在线建模主动噪声控制系统Fig.2 Eriksson’s secondary path online modeling active noise control system
在次级通道在线建模的方法中,Akhtar 的方法尤为显著,在降噪性能和系统稳定性方面取得了较高的性能。
Akhtar 对次级通道采用变步长的算法[4-5],在不增加第3个自适应滤波器的前提下,解决了建模信号对ANC系统稳定性的影响。Akhtar所提出的次级通道在线建模结构图3所示,以重构的误差信号f(n)作为次级路径建模滤波器和控制滤波器的输入误差信号,使用VSS-LMS算法对次级路径建模滤波器进行权系数的更新。开始时建模滤波器采用小步长,随着信号[d(n)-y′(n)]降低,采用大步长对建模滤波器的权系数进行更新,用以提升建模滤波器的收敛速度,进而提高整个系统的收敛速度以及降噪量。
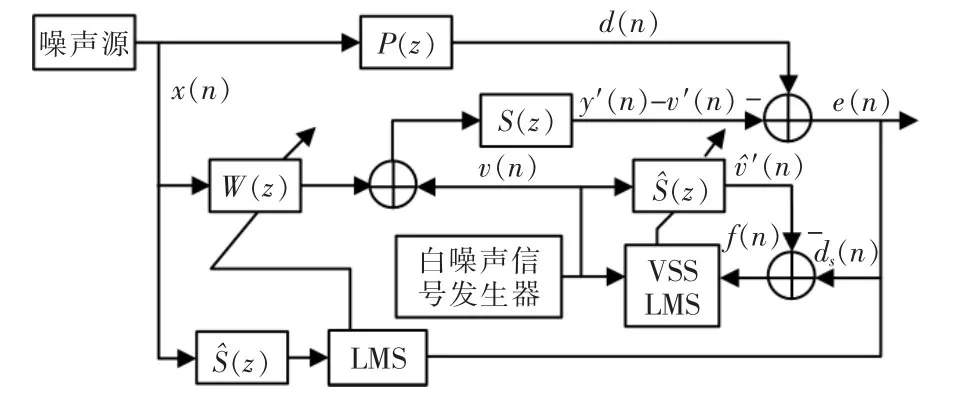
图3 Akhtar 提出的次级通道在线建模结构Fig.3 Online modeling structure of secondary channel proposed by Akhtar
假设,控制滤波器W(z)是长度为L 的实权值FIR 滤波器,次级信号y(n)为
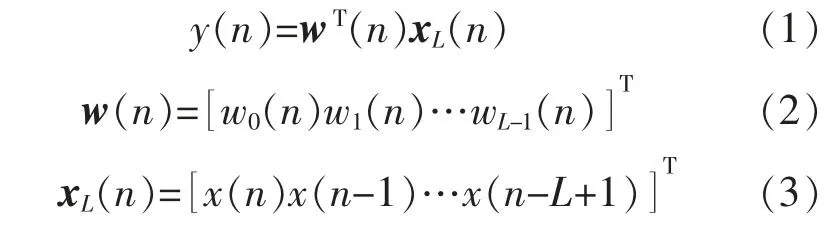
式中:x(n)为参考麦克风接收的参考信号。图中,v(n)为信号发生器产生的零均值高斯白噪声,与参考信号不相关。残余噪声信号e(n)为

其中
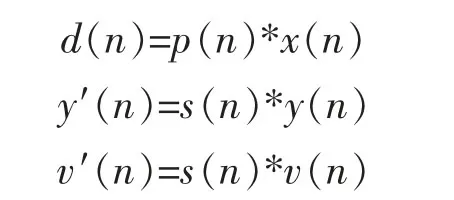
式中:d(n)为误差麦克风上接收的初级干扰信号;y′(n)为次级消除信号;v′(n)为建模信号;p(n)为主路径P(z)的单位脉冲响应;s(n)为次级路径S(z)的单位脉冲响应。信号f(n)作为控制滤波器W(z)和建模滤波器的误差信号,信号f(n)为
控制滤波器使用FxLMS算法进行权值更新:
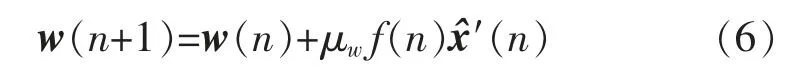
其中
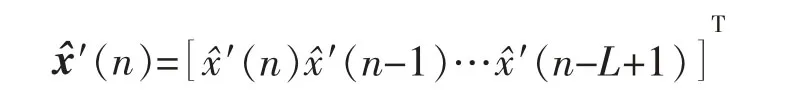
式中:μw为控制滤波器的步长;(n)为参考信号x(n)通过建模滤波器得来的滤波信号。
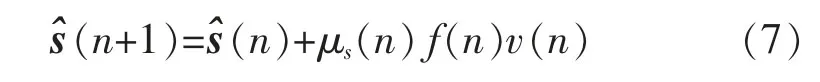
其中
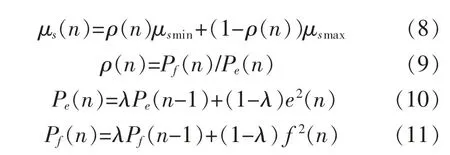
式中:μs为步长;μsmin,μsmax,λ 根据多次实验进行选择。根据式(8)对步长参数μs(n)进行更新;使用式(9)计算2个能量之比定义为ρ(n);使用式(10)估计参与误差信号的能量,使用式(11)估计建模误差信号f(n)的能量。
2.2 动量LMS算法
LMS算法在保证算法稳定的前提下,步长μ 的取值在0<μ<(1/λmax)之间,其中λmax为输入参考噪声信号x(n)自相关矩阵R 的最大特征值,R=E[x(n)xT(n)]。由于LMS算法对输入信号x(n)自相关矩阵的敏感性较强,故在此提出对次级路径采取基于动量LMS算法变步长次级通道建模方法。动量LMS算法在LMS算法基础上增加了2个动量项,减少了LMS算法对输入向量自相关矩阵特征值分散程度的敏感性。权值更新为
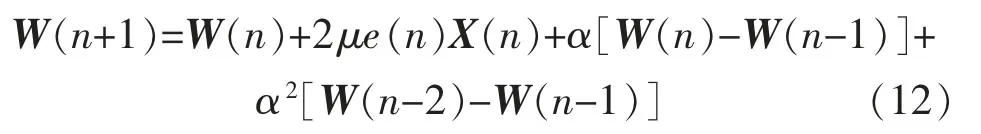
定义权系数误差向量为
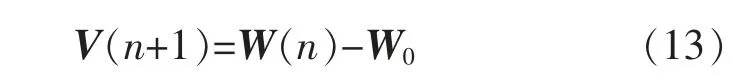
定义旋转权向量误差向量V′(n),设QQT=I,得
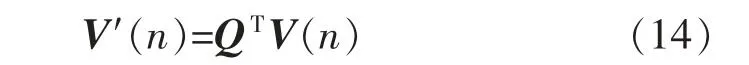
由于|βi|<1,可得0<μ<(1/λi),这正是LMS算法收敛因子的取值范围。当α≠0时,将两端点的值代入中,得出取值范围为

LMS算法在保证算法稳定的前提下,步长μ 的取值在0<μ<(1/λmax)之间,由式(15)可以得出,收敛步长μ 的取值范围较LMS算法增加了(1+α+α2)倍,在噪声信号频谱较宽时,LMS算法已经不能收敛时,动量LMS算法同样可以收敛,在α=0时,动量LMS算法就是LMS算法。
2.3 改进结构
Akhtar 提出的方法虽获得了较好的性能表现,但并没有完全消除建模信号对控制滤波器的影响,且变步长算法涉及大量浮点计算,不利于现场可编程门阵列FPGA(field-programmable gate array)实现。另外,在输入参考噪声信号的自相关矩阵特征值极度分散的情况下,控制滤波器中使用的LMS算法将出现收敛速度变慢的情况。因此,提出Akhtar 算法的改进方案,基于动量LMS算法的变步长次级路径在线建模ANC系统。该系统主要是对步长值采用梯度下降的方法,并使用建模精度ΔS 的变化来决定步长是否需要变化。其中改进方法1 的算法结构如图4所示。
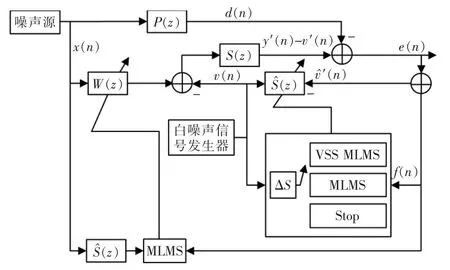
图4 方法1 主通道和次级通道最优变步长算法结构Fig.4 Structure of optimal variable step size algorithm for the primary and secondary channels in method 1
图中,降噪量及次级路径建模精确度为

在实际应用中并不能得到级次路径S(z)的权系数,也就无法得到ΔS,那么次级路径变步长算法的选择就无法进行,且由于VSS LMS算法中需要计算变步长μs(n),其中涉及到大量浮点数运算。为了降低方法1 中由于VSS LMS算法所带来的过高的计算复杂度,在此对方法1 进行改进,得到方法2,如图5所示。
在主动噪声控制系统中,参考噪声传感器获得参考信号x(n),误差传感器获得误差信号e(n)。为此构造函数Re,x(n)作为次级路径变步长的判断依据,为降低计算复杂度,避免硬件实现中出现浮点运算,每次Re,x(n)的计算只取前N个误差信号和前N个参考噪声信号,即
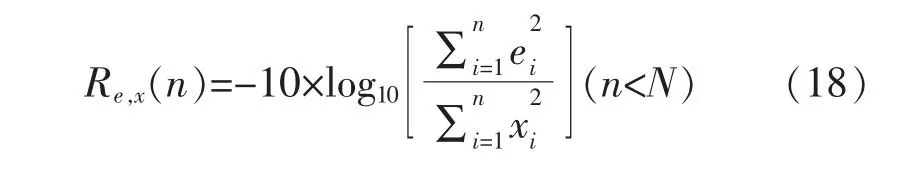

图5 方法2次级通道最优变步长算法结构Fig.5 Structure of optimal variable step size algorithm for secondary channels in method 2

式中:Re,x(n)为降噪量前N 项估计的实时值。同时设置2个下降阈值T1,T2。将控制滤波器中的动量LMS算法改为基本LMS算法。
其中,基于梯度下降的建模步骤如下:
步骤1初始阶段。检测函数Re,x 步骤2步骤1 虽然提高了建模收敛速度,但建模精度低。为保持原收敛速度并获得较好稳态误差,当T1≤Re,x(n) 步骤3当T2≤Re,x(n),停止加性高斯白噪声的注入,保持步长。即 在主动噪声控制系统中,参考噪声传感器获得参考信号x(n),误差传感器获得误差信号e(n)。为此,构造函数Re,x(n)作为次级路径变步长的判断依据,为降低计算复杂度,避免硬件实现中出现浮点运算,每次Re,x(n)的计算仅取前N个误差信号和前N个参考噪声信号,如式(18)(19)所示:Re,x(n)为降噪量前N 项估计的实时值,同时设置2个下降阈值T1,T2,将控制滤波器中的动量LMS算法改为基本LMS算法。 针对降噪性能和次级路径建模精度,对算法1,算法2,以及Akhtar 提出的算法在MatLab 中进行仿真验证。降噪量仿真如图6所示,算法1 和算法2在降噪量方面均比Akhtar 的方法好。次级通道建模误差仿真如图7所示,算法1 和算法2 在建模精度方面也比Akhtar 的建模精度高,达到相同建模精度时算法1 最优。其中,具体的结果对比见表1,表明所提2种算法均有良好的效果。 图6 降噪量的仿真Fig.6 Noise reduction simulation 图7 次级通道建模误差仿真Fig.7 Modeling error simulation of secondary channels 表1 本文方法与ANC 现有算法的性能比较Tab.1 Performance comparison between this paper and ANC existing algorithms 所提出的基于动量LMS算法的变步长次级路径在线建模ANC系统,减少了LMS算法对输入向量自相关矩阵特征值分散程度的敏感性。并为了获得更好的建模精度和稳定性,对步长值采用梯度下降的方法,使用建模精度的变化来决定步长是否需要变化。仿真结果表明,与现有方法相比,该改进的方法对ANC系统具有较好的降噪效果,对次级通道具有更精确的建模精度和收敛速度。
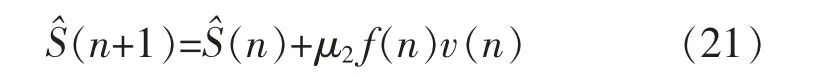
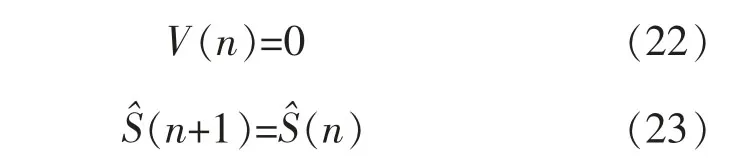
3 算法仿真与结果分析



4 结语
