《数学分析原理》中的方法探索与应用

（首都师范大学 北京 100048）

1 分析简介

本书由实数和复数的简单讨论开始 (第一章)，但这一章的最大亮点是在它的附录里：戴德金分割。它告诉你如何通过有理数来构造无理数。第二章是基本的拓扑知识，这些都是后面要用的。所以它们看似简单，但不能忽略。第三章中的数列和极限也是后面要用到的基本知识，这些对於中国的学生也许是不太难的。作者把极限的正式引入推迟到数列的收敛之后 (第四章)显然符合循序渐进的原则，也是国内大多数教材的思路。积分部分 (第六章)关于黎曼-斯蒂尔吉斯积分的一章是作者在第三版花了较大工夫的部分。这是在初等微积分的基础上对(实值、复值和向量值)积分概念的严格化。注意有些定理是基于黎曼积分进行讨论的。函数序列与函数项级数(第七章)是第三章中数列与级数的讨论的延伸。这可以说是本书最重要的部分了。本章要解决的是两个极限交换的问题，魏尔斯特拉斯一致逼近定理起了关键作用。有了第七章的准备，作者在下面的一章里讨论了一些特殊函数。第九章转到多元函数。本章里的线性算子就是泛函分析中的更为抽象的 Banach空间中的重要概念。第十章是微分几何导引。主要是Stokes定理。这里我主要想分享一些由书中知识点得到的一些联想和启发。

2 恒等式产生不等式的应用

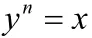
于是定理保证

y=supE

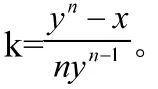
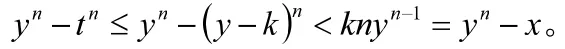
但y-k＜y，这与y是E的最小上界的事实矛盾。

应用延伸：下述极限存在且有限：

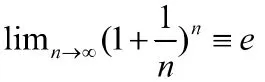
式中，e≈2.7182818称为自然底数。

证：令 b＞a＞0，有

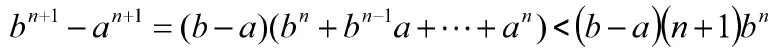
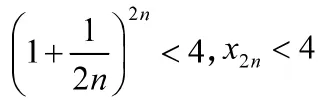
3 积分的引入

这个思路是几何学中的经典与精华：证明球的表面积和它半径与高度都相同的圆柱的表面积，严格来说，是没有上下两个面的圆柱。把圆柱展开成长方形，长方形的宽是圆柱底面的周长2 R，长方形的高是球的高度，也就是2R，不难发现，长方形面积即球面积表达式4 R2。问题是，球面怎么与柱面联系起来。基本思路是用许多覆盖球面的小长方形来估计表面积，然后再将这些小长方形直接向外投影，看看它们是什么样，就像是由放置在z轴上的小灯，朝着与xy平面平行的方向照出阴影一样。而令人惊讶的是，小长方形在圆柱面上的投影面积正好等于原始小长方形的面积。其实，这里有一个此消彼长的效应。我们把沿着纬线的边叫宽，沿着经线的边叫高。一方面，我们把小长方形向外投影时，它的宽会被放大。对于靠近两级的小长方形来说，这个长度被放大得很厉害，因为投影的距离相当长，而对于靠近赤道的小长方形来说投影几乎没有什么影响，但从另一方面来说，由于这些小长方形和z方向有一定角度，在投影过程中，小长方形的高会被缩小，在这种思路下，靠近极点的小长方形倾斜得很厉害，所以它们的高也会被挤压得很厉害，而靠近赤道的小长方形基本上和z轴平行，就不会被挤压太多。最终，这两种互相竞争的效果，也就是宽度上的拉伸和高度上的挤压完美地抵消了。当然，关键在于说明为什么两种竞争效果可以抵消。

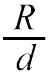
大体思路是把球面切成许多和xy平面平行的细环，然后对比这些环的面积和环在 xy平面上投影的面积。找到这些环的阴影和球面上偶数号的环之间的对应关系。用 表示环到球心连线和z轴的角度，把相邻环之间的角度差叫做d，也就是说，每个环的厚度是半径R乘d，这个环的内侧周长是2 Rsin，乘以厚度Rd，就是这个环的近似面积，当你把球面切得越来越细时，这个近似值也越来越准确。而其中一个环在xy平面上的阴影面积是2 Rsin cos d，而每一个环的阴影面积恰好等于球面上每一个环原始面积的一半，这里说的环不是阴影正上方的环，而是距离夹角为2的环（sin2=2sin cos）。即一个半球的表面积是两个同半径圆的面积，故一个球的表面积为四个相同半径圆的面积。

由此我们引入积分的公式及含义，这是读这本书时我所想补充的。

4 伟大的数学家Cantor

这就证明了A的每个可数子集是A的真子集。因此A是不可数集（否则A将是它自己的一个真子集，这不可能）。

以上证法的思想是Cantor首先使用的，并且称为Cantor的对角线手法。

叫做Cantor集。P显然是紧的，而且P不是空集。

如果k和m都是正整数，那么没有一个形式为

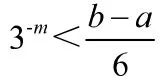
所以P不能含开区间。

Cantor集的一个非常有趣的性质是，它给我们提供了一个测度为0的不可数集的例子。

5 Lebesgue测度的建立

测度空间：假设X是一个集，它不必是欧式空间甚至任何度量空间的子集。如果存在X的子集（称它们为可测集）组成的—环，及定义在上的一个非负可数可加集函数称为测度），就说X是测度空间。

由我们所学概率论可以提出一个例子，事件可以看成是集，而事件发生的概率是可加（或可数可加）集函数。