一种瓦楞纸箱抗压强度的计算方法
2020-11-25巩桂芬刘雨杉孙德强
巩桂芬, 刘雨杉, 孙德强
(陕西科技大学 陕西省造纸技术及特种纸品开发重点实验室 中国轻工业纸基功能材料重点实验室 轻化工程国家级实验教学示范中心, 陕西 西安 710021)
0 引言
瓦楞纸箱是一种应用范围极广的包装制品,其消耗量一直是各种包装产品之首.瓦楞纸箱不仅能够保护产品,方便储运,还可以回收利用,属于绿色环保产品[1].为了确保流通过程中纸箱内部产品的质量与安全,纸箱的技术规格必须符合使用要求,其中抗压强度是检验瓦楞纸箱质量的关键指标之一,其大小对纸箱的安全性非常重要.瓦楞纸箱的抗压强度是指纸箱在试验机均匀施加的动态压力下可以承受的最大载荷和变形[2-4].
为了对瓦楞纸箱的抗压强度进行理论分析,很多学者从不同的方向推导了许多经验公式,例如Kellicutt公式、Mckee公式和Woff公式等[5].当瓦楞纸箱从上到下承受垂直载荷时,纸箱的侧板由于载荷的作用开始变形,直至完全破坏,这个过程称为侧板的失稳[6].结构稳定性的损失称为(结构)屈曲[7],瓦楞纸箱被压缩后发生变形并失去其原有的稳定性,这就是纸箱的屈曲.
现阶段纸箱抗压强度主要是通过经验公式进行计算,而对压缩过程的理论研究较少.结构稳定理论被广泛应用在建筑、土木、航空航天等领域,而将结构稳定理论应用在瓦楞纸箱的研究过程中较为少见.但了解纸箱屈曲原理,并将屈曲引入纸箱抗压强度的可靠性计算中,对于提高纸箱的可靠性,改善和优化纸箱设计都具有一定的作用.
1 瓦楞纸板简化模型
瓦楞纸板内有瓦楞芯纸形成的空心结构,属于夹层板,与普通正交各向异性薄板不同,为了方便研究,通常需要合理地简化瓦楞纸板的性能.贺妙欣等[8]将瓦楞纸板简化为单层各向同性的薄板,并通过理论计算和有限元分析,结果误差在5%以内,表明简化模型有效.故为了方便计算,本文也将正交各向异性的瓦楞纸板等效为各向同性的薄板,主要简化方法如下:
正交各向异性薄板在横向载荷q(x,y)作用下的挠度偏微分方程如下:
(1)
(2)
式(2)中:E1、E2-弹性主向下的拉压弹性模量;μ1、μ2-弹性主向所对应的泊松比;D1、D2-弹性主向下的抗弯刚度;D3-有效抗扭刚度;Dk-弹性主向下的抗扭刚度.
对于普通薄板其剪切主模量G12与弹性模量E存在以下关系:
(3)
即可以得到:
(4)
由式(3)和(4)等效各向同性薄板的力学常数为:
(5)
式(5)中:t-薄板厚度;D-抗弯刚度.其等效的各向同性板长宽尺寸x,y变换为[9]:
(6)
根据以上等效可以得到其抗弯刚度如下:
(7)
其挠度微分方程变为:
(8)
另q(x1,y1)=q1(x1,y1),将式(8)和D1、D2、D3代入式(1)中可得:
(9)
2 瓦楞纸箱临界屈曲载荷
2.1 薄板的压曲
在弹性力学中,平板是指被两个平行平面以及垂直于这两个平行平面的柱面所围成的对象,也可以简称为板[10].根据板的厚度可以将板分为三种:厚板、薄板和薄膜.瓦楞纸板属于薄板.
当薄板在仅受纵向载荷的作用时,其屈曲时关于挠度w的微分方程如下:
(10)
式(10)中:t为薄板的厚度,FTx、FTxy是拉力,FTy、FTyx为平错力或纵向剪力,又称为顺剪力.
当薄板从平面平衡状态进入弯曲状态时,挠度w从零开始变化,因此增加的形变势能与薄板的总弯曲应变势能相等.其功能方程如下:
W=Vε
(11)
而其中的弯曲形变势能Vε根据瑞利里茨法(Rayleigh-Ritz method)可知其有如下表达:
Vε=
(12)
纵向载荷所做的功W,可以根据由该载荷所引起的中面内力做的功来进行计算.FTx、FTy、FTxy表示的是载荷在板的任一微分块中的中面内力,如图1所示.
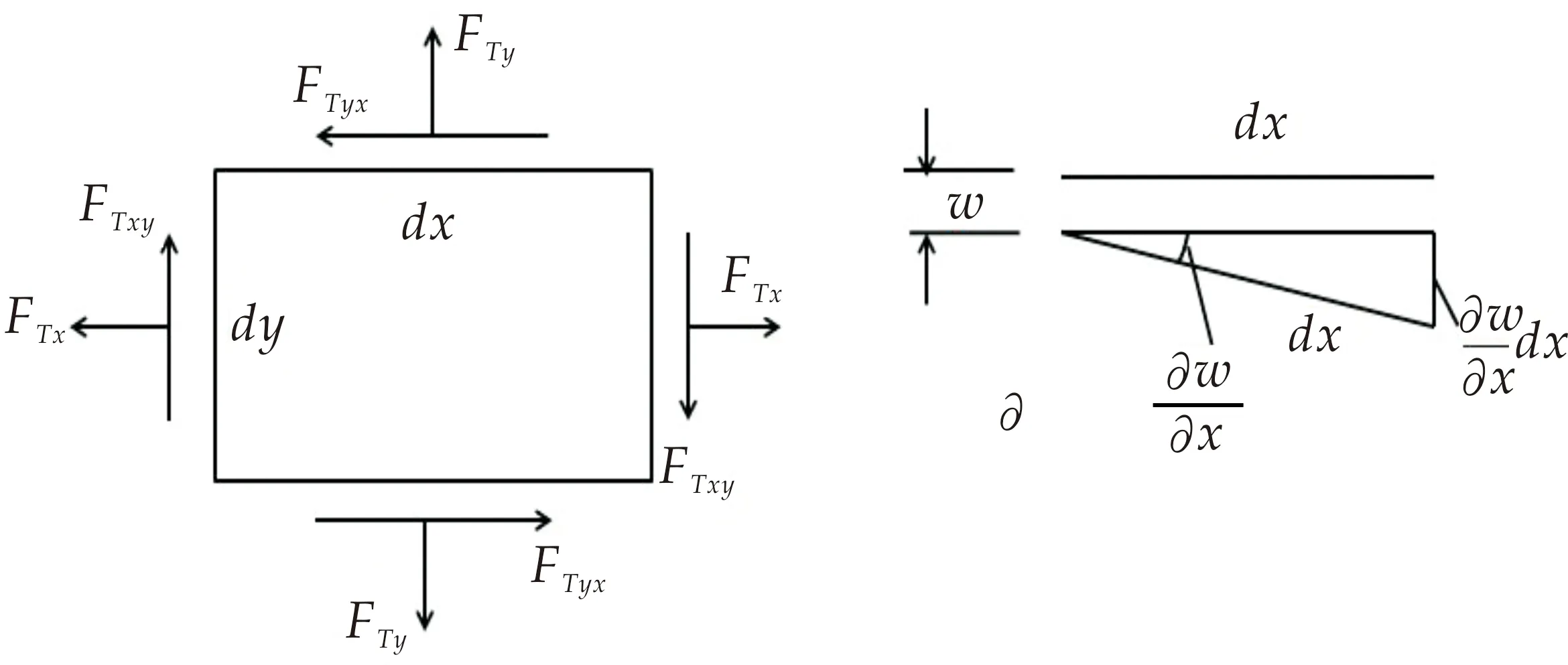
图1 中面内力微分图
设该微分块左右两侧的内力FTxdy初始距离为dx,当薄板弯曲后,这个距离则变为:
(13)
同样地,该微分块上下两侧的内力FTxdx所做的功为:
(14)
对于平错力FTxy=FTyx,可以计算出其45 °方向上的拉力和伸缩量,再利用式(13)和式(14),可以求得他们所做的功为:
(15)
该微分块中全部中面内力所做的功可以通过叠加上面三式得到:
(16)
由此可以得出整个薄板内的中面内力做的功,即纵向载荷压曲过程做的功:
(17)
为了获得更准确的临界载荷值,同时使得设定的挠度更好的符合临界载荷作用下的挠度,可以将挠度的表达式设定为:
(18)
式(18)中:wm是满足位移边界条件的挠度函数,Cm是与其互不依赖的待定系数.在选择合适的Cm时,可以使用最小势能原理.假设在平面平衡状态下薄板的形变势能和载荷势能都等于零,那么屈曲状态下薄板的形变势能就为Vε,载荷势能为V=-W,同时总势能为Vε+V,即Vε-W,于是可以根据最小势能原理求得:
(19)
为了使得挠度具有非零解,就必须令Cm具有非零解,因而上述齐次线性方程组的系数行列式就必须等于零,由此即可求得临界载荷的方程.
2.2 瓦楞纸板的临界屈曲载荷
瓦楞纸板的不稳定的形式属于分支点失稳,由于瓦楞纸板的主要使用范围在弹性范围内,且对于纸箱而言,其抗压强度一般发生在弹性末端,所以可以视为弹性屈曲.在压力试验中纸板只受到来自垂直方向的压力,其各边平面外的自由度和绕垂直边的面内转动自由度都是被约束的,因此可以将瓦楞纸板看作是四边简支的矩形薄板.静力学分析主要研究的是静止或者匀速状态下的结构响应,不考虑惯性和阻尼效应,以及时间有关载荷的影响.而在瓦楞纸箱实际抗压试验中,上压板运动速率在12±3 mm/min,上压板匀速运动且速率极低,所以可以将其视为静态载荷,此时纸板的屈曲为静力屈曲.因此,瓦楞纸板的屈曲可以看作是四边简支的矩形薄板在静载荷的作用下发生的弹性、静力、分支点屈曲.求解瓦楞纸板的临界屈曲载荷,即可简化为求解四边简支的矩形薄板的临界载荷[11].
同时对于质量合格的瓦楞纸板在压缩过程中不涉及脱胶问题,粘合剂对压缩过程的影响甚微,故本文在对纸箱抗压强度的研究中忽略粘合剂的作用.
如图2所示,设四边简支的矩形薄板两对边承受均布压力,即纵向载荷,其在板的每单位长度上可以表示为Fx,其中面内力可以表示为:
FTx=-Fx,FTy=0,FTxy=0
(20)
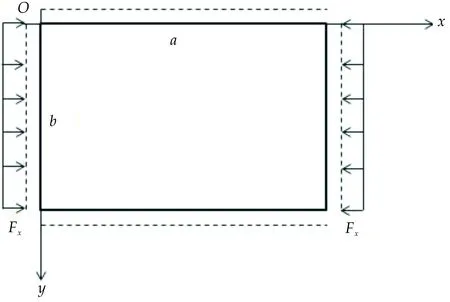
图2 四边简支均匀受压薄板
法国力学家纳维提出的纳维解法,是利用双三角级数求解薄板弯曲边值问题,纳维将挠度w的表达式定义为如下的重三角级数:
(21)
该式的物理意义为:当薄板在载荷作用下,x方向会变成m个半波,y方向会变成n个半波,Amn表示的是挠度的波幅,其中,m、n为任意正整数.将式(21)代入到式(12),并对x的积分从0到a,对y的积分从0到b,最后可以得到:
(22)
同时也将式(20)和(21)代入到式(16)中,可以得到:
(23)
而式(19)在此就变成了:
(24)
再将式(22)和(23)代入,可以求得:
(25)
令这个方程的系数行列式,即方程的唯一系数等于零,可以求得薄板临界载荷的表达式为:
(26)
式(26)中:m、n可以取任意整数.在一切可以满足以上条件的纵向载荷中间,数值最大的即为临界载荷,由式(26)可见,当n增加时,Fx增加,所以应该取n=1,这也就表示在压曲后,薄板沿着y方向只有一个正弦半波,所以令n=1,代入求解式(26),得到临界载荷:
(27)
或
(28)
其中:
(29)
依次命m=1,2,3,…,针对每一个m的值,都可以由式(29)计算出a/b取不同值时的k值,得到如图3所示的一组曲线.
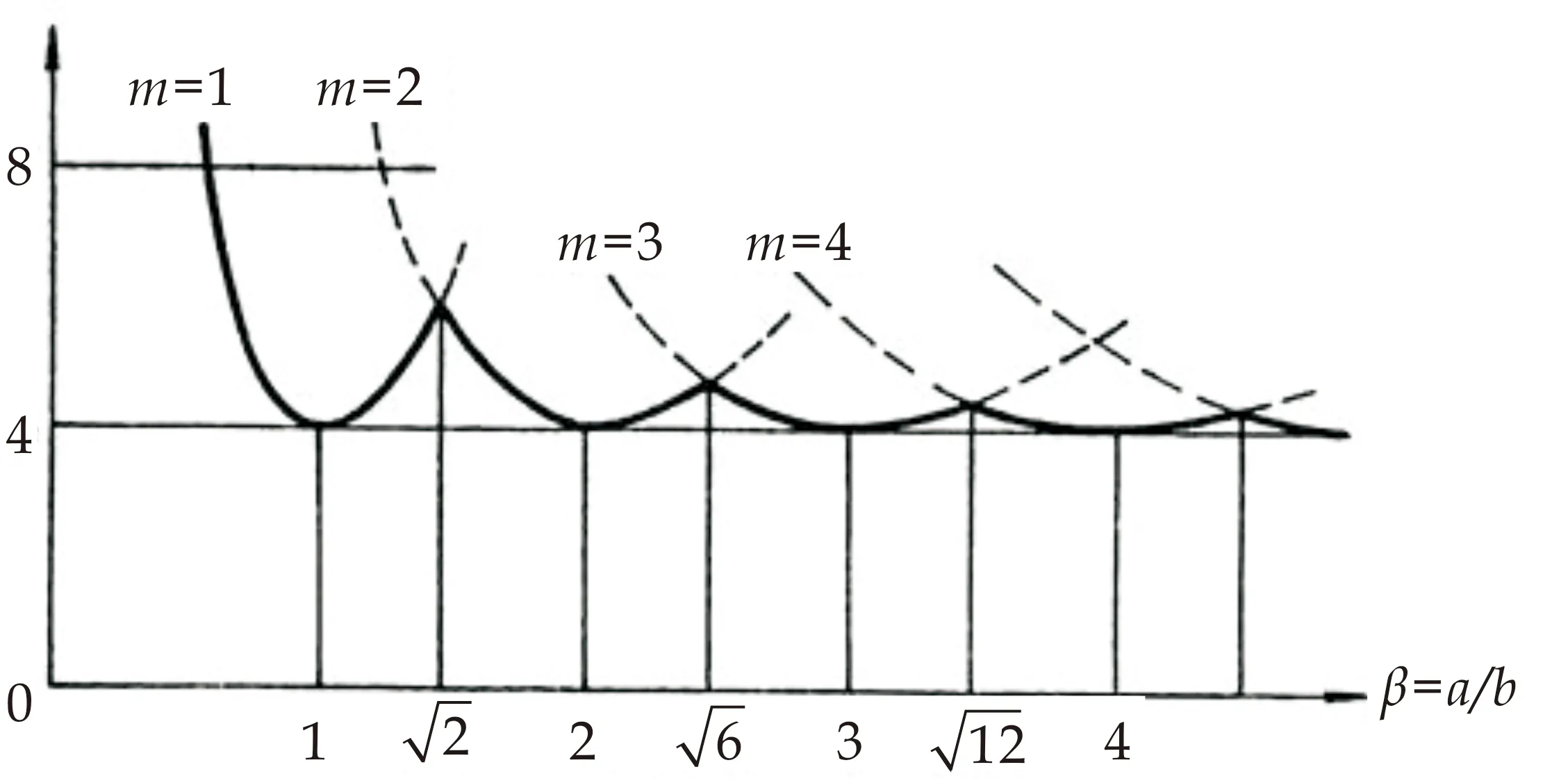
图3 K值与板件长宽比的关系
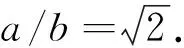
(30)
2.3 瓦楞纸箱的临界屈曲载荷
瓦楞纸箱的结构破坏形式主要是纸箱的失稳,在理论计算时通常是先对纸箱进行合理的简化,再参考一定的经验公式,求出在弹性范围内,即纸箱使用范围内的临界屈曲载荷.瓦楞纸箱的失效分析可以简化为四个侧板在压力下的弹性屈曲,因此整个瓦楞纸箱的最大承载能力可以使用侧板的临界屈曲载荷来反向运算.在抗压强度的测试中,纸箱的上表面受到缓慢增加的压力,随着压力的增加,纸箱的变形量也会持续增加.而承受压力的主要构件是纸箱的侧板.如果负载增加到某个阈值,则纸箱的侧板将会产生横向挠曲并失去原有稳定性,此时的负载即为临界屈曲载荷.纸箱由瓦楞纸板制成,纸箱的屈曲载荷与纸板的临界载荷密切相关,瓦楞纸箱的屈曲载荷可以近似为[12]:
(31)
式(31)中:Pm是瓦楞纸板的边压强度,L和w分别是纸箱的长度和宽度,PcrL和PcrW分别是纸箱相应长方向和宽方向侧板的临界载荷.C和b是马基提出的半经验公式中的经验常数:
(32)
式(32)中:PZ为单位板宽的压损强度,PZ=BCT/Z,Z为纸箱周长,代入公式(30)、(31),得到瓦楞纸箱抗压强度的计算公式:
(33)
式(33)中:L1、W1、H1分别表示将正交各向异性的瓦楞纸板等效后所得的长宽高尺寸参数.
3 算例
3.1 瓦楞纸箱物理试验
试验材料选择陕西天成纸业有限公司生产的瓦楞纸板,瓦楞形状为UV形,瓦楞楞型为B型,面纸、芯纸和里纸的定量分别为160 g/m2、130 g/m2和 160 g/m2;纸箱箱型为0201,尺寸为240 mm×192 mm×192 mm.试验前对试样进行预处理,按照GB/T 4857.2-2005的要求将试样在23 ℃、相对湿度为50%的恒温恒湿试验室中处理48 h.
对瓦楞原纸(芯纸、面纸、里纸)进行拉伸试验以获得瓦楞纸板的弹性参数,每组试验样品数量为5.对瓦楞纸板进行边压强度试验,试验样品数量为10.对瓦楞纸箱进行抗压强度试验,样品的数量为5,使用胶带对纸箱进行密封,避免在密封过程中损坏纸箱.有关拉伸试验参照GB/T 1040.4-2006.边压试验参照GB/T 6546-1998.有关使用压力测试仪的压缩和堆叠测试方法,参见国家标准GB/T 4857.4-2008.
试验中所用到的设备有:纸与纸板厚度测定仪(PN-PT6)、CMT4304微机控制电子万能试验机、PN-CT300B型压缩强度试验仪、纸箱纸盒电脑打样机(DCZ-2516,AOK)、CMT5504-BZ微机控制电子万能试验机.
试验后纸板的弹性参数如表1所示.表1中的X、Y、Z方向分别是指是纸张纤维方向(X方向)、垂直于纤维的方向(Y方向)、面外方向(Z方向).
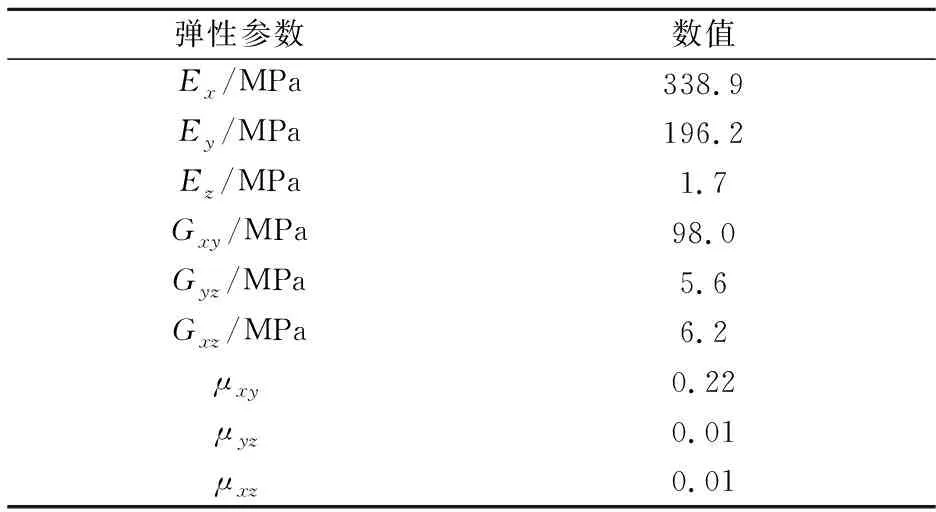
表1 瓦楞纸板的弹性参数
取10次边压试验结果的平均值可以得出纸板的边压强度为2 689 N/m.取5次抗压试验结果的平均值可以得到瓦楞纸箱的抗压强度为1 503.24 N.
3.2 瓦楞纸箱抗压强度计算
本文用于试验的瓦楞纸箱尺寸为240 mm×192 mm×192 mm,厚度t=3 mm,其侧面可视为由四块瓦楞纸板构成,侧板两两对称,故可视为由尺寸240 mm×192 mm和192 mm×192 mm的两类薄板组成,并将240 mm×192 mm尺寸称为长方向板,将192 mm×192 mm尺寸称为宽方向板.根据式(1~9)的等效原则,将长宽两方向板均等效为各向同性薄板,薄板的弹性参数如表1所示.
简化后的各向同性长方向板的尺寸变为:240 mm×220 mm,各向同性宽方向板的尺寸变为:192 mm×220 mm,其弹性参数变为:
E=338.9 MPa,μ=0.046.
联立式(31)和(32)并将试验所得的纸箱抗压强度BCT、纸箱周长Z、侧板临界载荷Pcr的值代入到Excel中拟合,得到该瓦楞纸箱的经验常数:C=0.75,b=8.3.再代入公式(33)可以得到理论计算出的瓦楞纸箱抗压强度为1 360.11 N.
将理论计算的临界载荷和抗压试验得到的抗压强度值进行对比,如表2所示.

表2 瓦楞纸箱抗压强度的理论计算与试验误差
理论计算结果与试验结果之间的误差是9.5%,证明利用结构稳定理论对瓦楞纸箱的抗压强度进行计算的方法具有一定的参考价值.
4 结论
通过结构稳定理论将正交各向异性的瓦楞纸板等效为各向同性的薄板,建立四边简支的薄板等效模型,使用能量法,推导出瓦楞纸板的功能方程求出纸箱的临界屈曲载荷.通过对比理论计算与试验结果的差异,可以看出利用结构稳定理论计算瓦楞纸箱的抗压强度具有一定的参考价值,得到了适用于瓦楞纸板的屈曲微分方程,建立了纸箱失稳的理论基础,为瓦楞纸箱抗压强度的理论研究提供了依据.
