ACC车辆跟驰建模及模型特性分析

秦严严，王 昊，何兆益，冉 斌

(1.重庆交通大学 交通运输学院，重庆 400074； 2. 东南大学 城市智能交通江苏省重点实验室，江苏 南京 210096；3. 美国威斯康星大学麦迪逊分校 土木与环境工程系，威斯康星州 麦迪逊 53706)

0 引 言

自适应巡航控制(adaptive cruise control, ACC)车辆能够依托车载传感设备，检测前车行驶状态，进而根据自身当前行驶速度等信息，优化下一个时刻的输出加速度，达到车辆自主式行驶的目的[1]。ACC车辆能够将传统人工驾驶员从繁重的驾驶任务中解脱出来，同时作为未来智能网联环境下智能车辆的第一个市场阶段，有望最先在实际道路中大规模行驶，因此针对ACC车辆的相关研究更具实际的现实意义。ACC车辆关注于车辆的纵向行车控制，有关ACC车辆跟驰建模的研究已经成为目前国内外的研究热点[2]，鉴于此，笔者针对ACC车辆跟驰模型的建模工作开展研究。

依据国内外现有研究成果，从交通工程学的角度，针对ACC跟驰模型的建模工作可以归纳为以下几类：①加州大学伯克利分校研究团队提出了恒定车头时距的ACC跟驰模型[3]，所提模型结构简单且模型参数物理意义明确，因此得到了广泛的应用；②A. KESTING等[4]应用智能驾驶员模型作为ACC车辆跟驰模型，取得了众多的研究结果，并得到了较多学者的认可；③国内研究人员[5]从元胞自动机的角度出发，构建了用于描述ACC车辆跟驰特性的元胞自动机模型，扩展了ACC跟驰建模思路。其中，由加州大学伯克利分校团队所提的ACC跟驰模型影响力较大，是目前常用的ACC跟驰模型。但该模型中恒定车头时距策略体现的期望车头间距是关于速度的线性函数，有学者指出这种跟驰策略具有通行能力受到期望车间时距约束的缺陷，同时易对模型稳定性造成负面影响[6]。但是鲜有文献针对加州大学伯克利分校所提ACC模型进行改善研究。鉴于此，笔者从车头间距随速度非线性动态调整的角度出发，对加州大学伯克利分校所提ACC模型进行改进，提出基于非线性动态车头间距的ACC跟驰模型，为ACC建模研究提供模型参考。

需要说明的是，目前ACC车辆交通流实测数据尚不普及，在没有ACC车辆交通流实测数据的情况下，笔者对ACC跟驰模型的研究着重于模型改进前后在理论分析层面的对比。鉴于原ACC跟驰模型的应用场景为高速公路交通流场景，笔者改进ACC跟驰模型的未来应用场景仍然设定为高速公路交通流场景。

1 跟驰建模

加州大学伯克利分校研究团队针对ACC车辆交通流模型开展了大量的研究工作，其提出的ACC车辆跟驰模型得到普遍认可与应用，该ACC跟驰模型如式(1)[3]：

vn(t)]

(1)

由式(1)可以看出，加州大学所提ACC模型为恒定车头时距策略的跟驰模型，其具备模型结构简单、便于应用的优点，同时模型参数也具有物理意义明确的优点，这使得该ACC模型被广泛应用于ACC车辆对交通系统影响的研究中。但是，由于模型结构过于简单以及恒定车头时距的固有属性，该模型同样存在两个方面的缺陷：

1)在交通流均衡态方面，根据该ACC模型推导出的流量-密度基本图曲线对ACC车辆期望车间时距取值的依赖性较大。而ACC期望车间时距是可以根据乘客喜好进行调节的，反应了乘客的乘车喜好差异性。由于均衡态基本图在理论层面决定了ACC对交通流通行能力的提升程度，因此在该ACC模型背景下，乘客的乘车喜好差异性能够较多地干预道路通行能力水平，不利于有效评估未来ACC车辆对通行能力的影响作用。

2)在交通流非均衡态方面，即当ACC车辆在前方干扰下偏离均衡态过程中的稳定性方面，该ACC模型存在稳定性较差的缺点[3]，跟驰模型的稳定性是车流运营质量的内在机理，较差的稳定性对道路运营质量存在一定的负面影响，因此，较好的稳定性是跟驰模型优劣评价的一个重要指标。

鉴于此，笔者针对式(1)中ACC模型的上述两个方面的缺陷，在兼顾该ACC模型结构简单且参数物理意义明确的前提下，提出新的ACC车辆跟驰模型。如前所述，式(1)中的ACC跟驰模型属于恒定车头时距策略下的建模思路，在该建模思路下，无论车辆当前的速度如何，其车头时距均为固定值，即期望车头间距是关于速度的线性函数。然而在实际交通场景中，较高的车速要求车辆保持相对较大的车头时距，而当车辆行驶速度较慢时，车辆能够安全地以较小的车头时距行驶。此特性要求ACC跟驰建模的思路应当是非线性动态车头间距策略，即期望车头间距是关于速度的非线性函数。在文献[7]的研究成果基础之上，随速度变化而非线性动态调整的期望车头间距为：

(2)

式中：hd(t)为t时刻期望车头间距；vf为最大行驶车速，取值33.3 m/s。

在加州大学伯克利分校研究团队所提ACC跟驰模型基础之上，笔者建立ACC跟驰模型如式(3)：

vn(t)]

(3)

由式(3)可以看出，笔者所建立的ACC跟驰模型应用非线性动态车头间距策略，能够使得期望车头间距随速度非线性地动态调节，另一方面保留了原ACC模型的模型结构，使得所提ACC跟驰模型同样具备模型结构简单且模型参数物理意义明确的优势。

2 模型均衡态特性

均衡态反应了连续车流在不受干扰情况下的平稳行驶状况。均衡态特性往往通过基本图模型来反映。基本图模型能够从理论层面解析道路通行能力影响作用，而通行能力分析在交通工程应用中具有现实的实际意义[8-10]。因此，本小节计算所提ACC跟驰模型对应的基本图模型，并从通行能力的角度与原ACC模型进行对比分析，理论论证所提ACC模型具备的模型优势。

在笔者所提ACC模型中，如式(3)，在均衡态条件下，模型均衡态车头间距为：

(4)

式中：h为所提ACC模型在均衡态下的车头间距；v为均衡态速度。

根据密度的定义，计算得到所提ACC模型下的交通流密度k为：

(5)

根据式(5)，将速度表达成关于密度的函数，如式(6)：

v=vf[1-k(l+s0)]

(6)

基于交通流流量q等于密度k与速度v乘积的基本关系式，得到笔者所提ACC模型的流量-密度基本图模型，如式(7)：

q=vfk[1-k(l+s0)]

(7)

根据上述推导步骤，同样能够得到原ACC模型下的流量-密度基本图模型，如式(8)：

(8)

在车辆静止状态，车流速度为零，此时可通过式(5)计算得到拥挤密度为142.86 veh/km，而当车流按照最大行驶速度时，根据式(4)可认为车辆之间车头间距无穷大，对应密度为零。在密度从零变化至拥挤密度的过程中，根据式(7)和式(8)，可分别计算得到笔者所提ACC模型以及原ACC模型下的流量-密度基本图曲线，如图1。

图1给出了笔者所提ACC模型下的基本图曲线与原ACC模型下的基本图曲线的对比，并且给出了原ACC模型在T分别取值1.1、1.6、2.2 s时的情况。由图1可以看出，笔者模型下的基本图曲线在原模型基本图曲线的右上方，表明了笔者所提ACC模型对通行能力的提升更为显著，可以分别计算得到笔者所提ACC模型与原ACC模型的最大通行能力，以及最大通行能力对应的临界速度与最佳密度值，如表1。

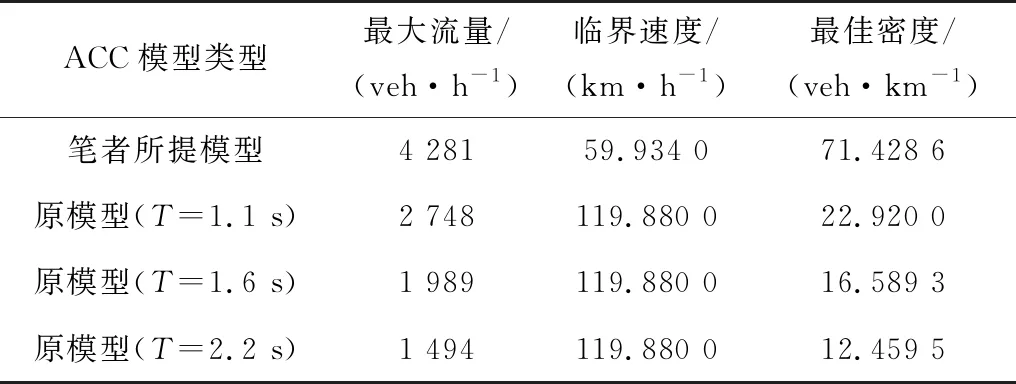
表1 基本图最大流量、临界速度与最佳密度

由表1可知，笔者所提ACC模型最大通行能力可达4 281 veh/h，约为T=1.1 s时原模型最大通行能力的1.557 9倍，是T=2.2 s时原模型最大通行能力的2.865 5倍，表明了所提ACC模型相比原模型在最大通行能力方面的改善。进一步地，从表1中可以看出，笔者所提ACC模型在最大通行能力时的临界速度与最佳密度分别处于最大速度与拥挤密度的适中值范围。原ACC模型只有在车流处于较高的速度下，以较低的密度状态行驶时，才能够达到最大通行能力状态。而从基本图曲线上看出，拥挤态区域明显比非拥挤态区域对应的密度范围大，这使得原模型通行能力的提升受到限制。

此外，笔者所提ACC模型基本图曲线与原模型曲线存在交点，即分别为图中A、B、C 3个交点。A、B、C 3点处的流量、速度与密度状态值可由基本图模型公式计算得到，如表2。

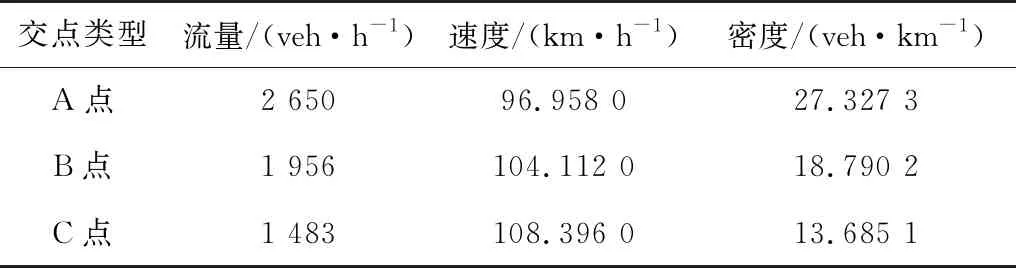
表2 交点处的流量、速度与密度

对于A点而言，对应密度为27.327 3 veh/km。在密度高于27.327 3 veh/km时，笔者所提ACC模型总比原模型的流量大，即相同密度水平下的通行能力高；在密度低于27.327 3 veh/km的范围内，笔者所提ACC模型通行能力低于原模型，但是相差不大，可视为基本相当。对于B点和C点而言，所得结果与A点情况类似。因此，从整体上看，笔者所提ACC模型在通行能力方面明显优于原模型，并且笔者所提模型通行能力的提升不受原模型中期望车间时距参数T的影响，表明了笔者所提ACC模型在通行能力方面达到了预期效果。

3 模型非均衡态特性

均衡态的车流在受到下游扰动时，会偏离均衡态，造成一定的速度波动，当扰动结束后，车流能否再次回到均衡态的过程体现了非均衡态特性，即车流稳定性。稳定的车流能够应对下游扰动，不稳定的车流则易造成上游速度波动过大，形成交通震荡甚至诱发交通拥堵并对交通安全造成负面影响[11]。因此，从非均衡态角度来看，跟驰模型的好坏主要体现在模型是否具备较好的稳定性。本小节理论推导笔者所提ACC模型的稳定性条件，并与原模型在稳定性方面进行对比，从理论上论证所提ACC模型具备的稳定性优势。

针对笔者所提ACC模型，如式(3)，在均衡态对其进行线性化，计算结果如式(9)：

(9)

式中：ve与he为均衡态速度与车头间距。

在车流处于均衡态时，所有车辆的位移均为均衡态位移，在扰动干扰下，车辆位移偏移均衡态，即：

(10)

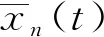
针对式(10)进行关于时间t的微分计算，可得：

(11)

将式(11)带入式(9)中，计算得到：

(12)

将扰动rn(t)用傅里叶形式表达，即：

rn(t)=Aexp(ikm+zt)

(13)

将式(13)带入式(12)中，并计算得到：

(14)

然后，将z展开为z=z1(ik)+z2(ik)2+…，并且带入式(14)中，计算系数z2为：

(15)

则当z2大于0时，跟驰模型稳定，否则，不稳定。则化简式(15)计算得到所提ACC跟驰模型稳定的判别条件如式(16)：

2(vf-ve)4>0

(16)

根据上述稳定性理论推导过程，同样能够计算得到原ACC模型稳定时应满足的条件为：

kdT2+2kvT-2>0

(17)

由式(16)可知，笔者所提ACC模型稳定性与均衡态速度有关，而原ACC模型稳定性与均衡态速度无关，仅与期望车间时距参数T有关，并且T取值越大，式(17)左边项的值越大，越有利于模型趋于稳定。将式(16)和式(17)中的左边项看作模型稳定性条件，分析得到笔者所提ACC模型以及原ACC模型的稳定性情况，如图2。

从图2中可以看出，原ACC模型在T取最小值1.1 s和最大值2.2 s时，均不能稳定，而笔者所提ACC模型可在所有均衡态速度范围内实现稳定，这表明了笔者所提ACC模型在非均衡态的稳定性问题上比原ACC模型更具有模型优势，理论证实了笔者所提ACC模型在稳定性方面的预期效果。

4 结 语

1)考虑非线性动态期望车头间距，对加州大学伯克利分校所提ACC跟驰模型进行了改进，建立了基于非线性动态车头间距策略的ACC跟驰模型。笔者所提ACC模型同样具备模型结构简单且模型参数物理意义明确的优点，并从均衡态的通行能力和非均衡态的稳定性两个方面，论证了笔者所提ACC模型比原模型具备更优的模型特性。

2)笔者所提ACC模型通行能力不再依赖期望车头时距的参数设定，改善了原模型受期望车头时距参数限制而不能有效提升通行能力的不足。笔者所提模型能够有效提升道路通行能力，最大通行能力可达4 281 veh/h，是原模型最大通行能力的约1.56～2.87倍。同时，与原模型相比，笔者所提模型具备良好的稳定性，能够在任意均衡态速度下保持稳定状态，改善了原模型稳定性较差的缺陷。

3)研究结果可为未来ACC车辆的建模研究以及大规模实地测试的实施提供模型参考。在ACC跟驰建模的基础之上，面向车联网环境下的智能网联车辆跟驰建模需要考虑更多的车联网环境特性，是下一步的研究内容。同时，未来ACC车辆交通流实测数据普及之后，应用ACC车辆交通流实测数据研究笔者改进ACC模型的适用性场景，值得进一步研究。