四面体单元阶次及细化对L形套筒弯杆强度计算结果的影响
2020-11-24李波
李 波
(安徽粮食工程职业学院 机电工程系,合肥 230011)
传统的工程产品结构设计多采用经验公式验算,再试制样品经过试验反复修正,这种设计和验证方法工作量大、投入高、研发周期长。随着计算机技术的成熟及数值计算方法的完善,融合计算机技术及实用数值分析方法的有限元法在产品结构设计上得到了广泛应用,现已成为航空、机械、土木结构等领域工程分析必不可少的计算工具。通过产品结构的有限元分析,能够有效缩短产品开发周期,降低开发成本[1]。有限元仿真过程中,有限元模型的建立占整个仿真过程80%的时间,其中建模质量对计算结果有较大影响,建立高置信度的有限元模型至关重要。为此,本文以L形套筒弯杆为例,探讨有限元分析建模中涉及到的问题,研究结果对于工程产品尤其大型复杂零件的有限元建模具有十分重要的意义。
1 有限元法研究思路及软件分析流程
1.1 有限元法研究思路
有限元法采用“先分后合”的基本思想,即根据结构的特点,选取适当的单元形式,将连续的结构体离散为有限个单元体,单元之间以节点相连;然后选择节点的物理量作为未知量,对每一个单元选择一个简单的连续的插值函数,近似表达出单元内任一点的物理量;其次,利用有限元法的不同解法,形成单元性质的矩阵方程[2],再建立整个物体的平衡方程组,形成整体刚度矩阵,最后引入边界条件,求解出节点上的未知量,从而可求出结构的应力、应变等参数。
1.2 软件分析流程
基于有限元法开发的CAE分析软件能够显著提高产品的结构性能,缩短研发周期,提高产品的市场竞争力。本文对L形套筒弯杆分析采用了HyperWorks进行仿真分析,HyperWorks作为一款大型国际通用CAE分析软件,集成了设计与分析所需的各种工具,建模方便快捷[3],其前处理模块——HyperMesh具有强大的前处理功能,视图界面友好,提供丰富的CAD软件数据接口,能够直接导入CAD软件(如UG 、 Pro/E、SolidWorks等)生成的几何文件或已有的有限元模型,模型几何清理、修复及网格划分功能强大[4],在工程分析前期建模中应用广泛。HyperMesh软件用户界面如图1所示。
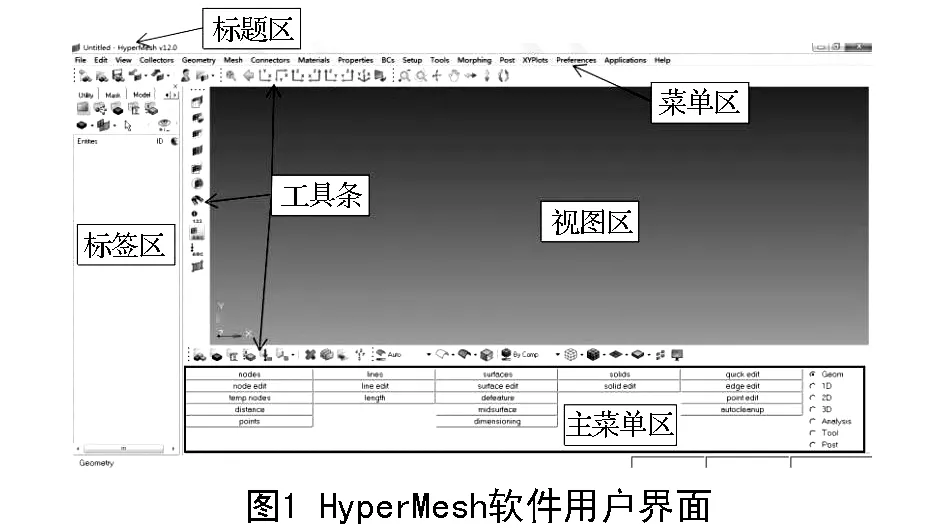
CAE分析软件的实施过程包括前处理、计算、后处理3阶段,前处理完成模型几何处理、网格划分、属性定义、边界条件施加等,形成有限元计算模型;计算过程则是利用求解器进行求解计算;后处理即查看分析结果,对分析对象的性能或设计合理性进行分析与评估,从而进行改进、优化[5]。CAE分析主要步骤如图2。
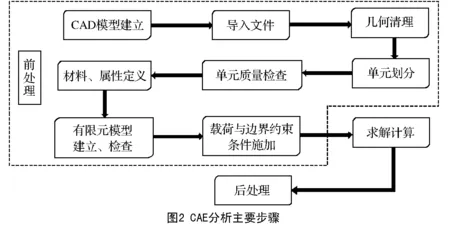
2 L形套筒弯杆有限元建模
2.1 结构几何模型建立及属性
利用3维CAD建模软件——SolidWorks建立L套筒弯杆实体模型,模型简化后生成step格式文件并导入前处理器——HyperMesh中进行建模处理[6]。几何模型如图3所示。L形套筒弯杆为典型的方头圆杆结构,质量为0.68kg,材质为合金钢。材料参数:弹性模量210GPa,泊松比0.3,密度7.9g/cm3。


2.2 模型结构离散
在实际工程应用中,四面体实体网格适应性强,尤其对于大型复杂零件的结构离散应用广泛,因此,本文着重以四面体网格为例,考察四面体网格阶次及网格细化对计算结果的影响,即采用3.0、2.5、2.0、1.5、1.0mm大小的1阶和2阶四面体网格分别对L形套筒弯杆进行结构离散,得到10个不同阶次、不同网格尺寸的离散模型,离散后的四面体网格局部显示如图4。其中,1阶四面体单元为4节点,2阶四面体单元为10节点,单元节点分布分别如图5和图6所示。离散后模型参数如表1。
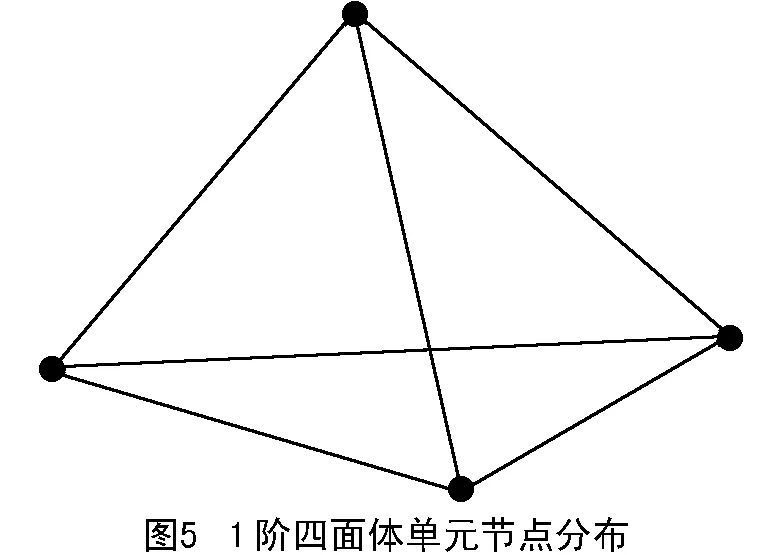
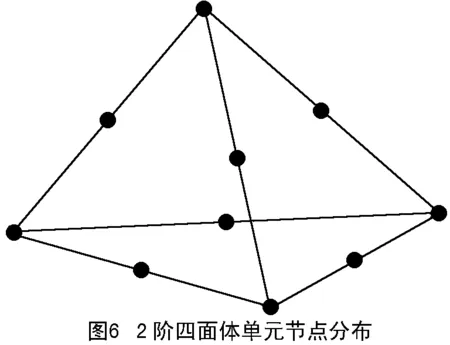
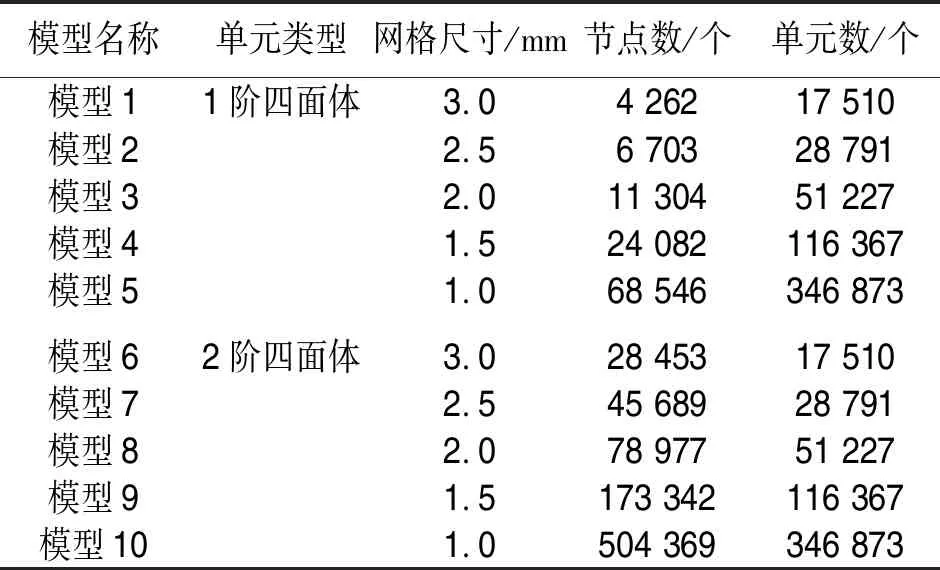
表1 L形弯杆离散后模型参数
2.3 边界条件设定
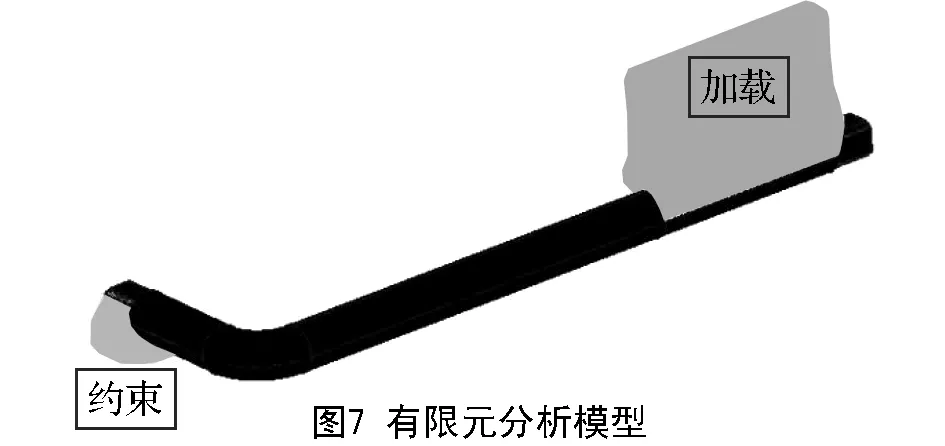
对L形套筒弯杆按常规套筒扳手加载形式进行静强度分析,假定长杆为加载端,施加边界条件如下:对短杆端部进行6个方向自由度全约束,在长杆端部施加垂直于杆件的载荷F=250N。建立有限元分析模型如图7。
3 有限元计算及结果分析
3.1 计算结果
为研究不同四面体网格阶次及网格细化对结构静强度结果的影响,现对10个模型施加相同载荷与边界约束,使用软件自带的OptiStruct求解器分别求解计算。由分析结果知,L形弯杆弯角位置为结构薄弱部位,存在最大应力;长杆受力产生弯曲,端部有最大变形量。当网格尺寸为3mm和1mm时,结构薄弱区域最大应力及变形情况分别如图8~图15所示。不同模型计算结果如表2所示。
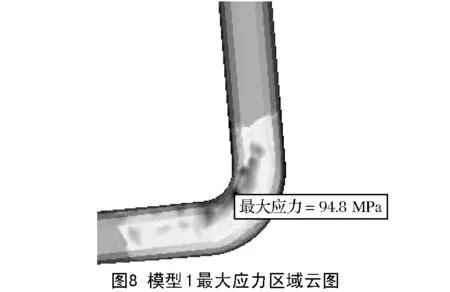

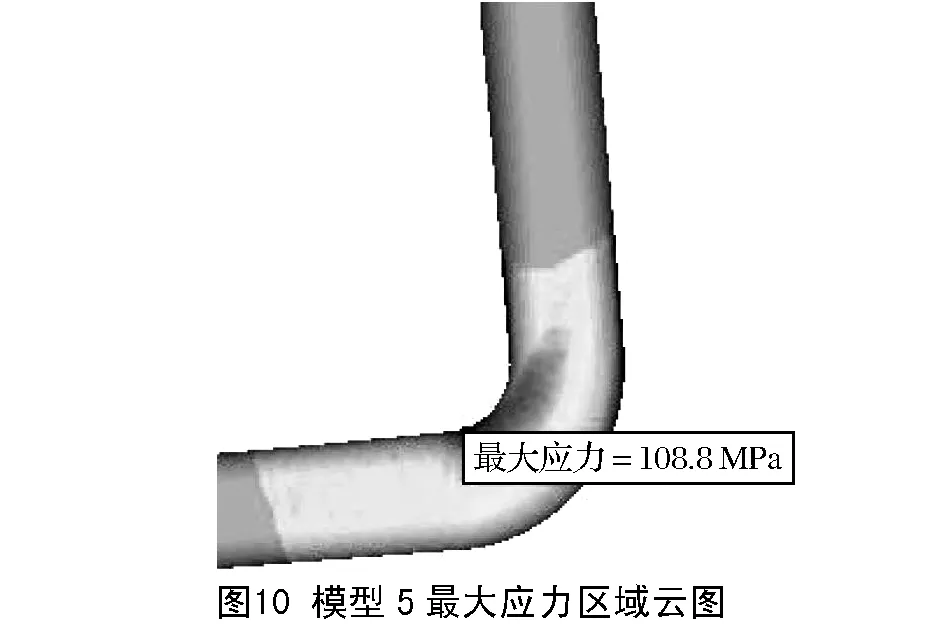
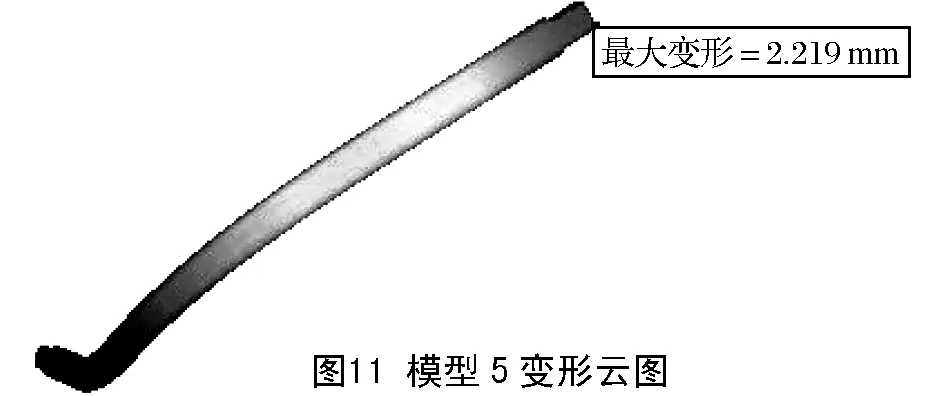
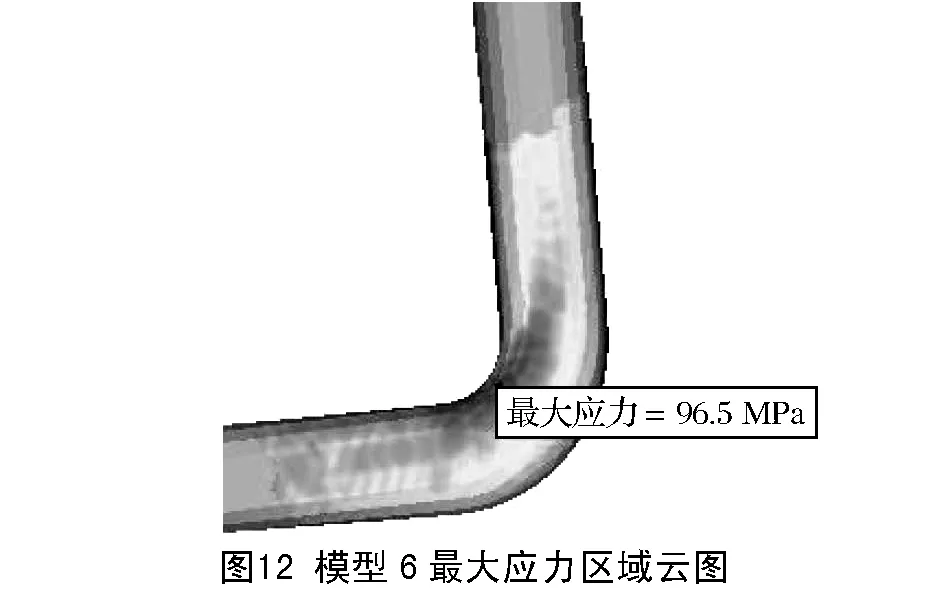
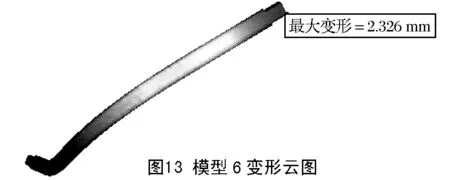
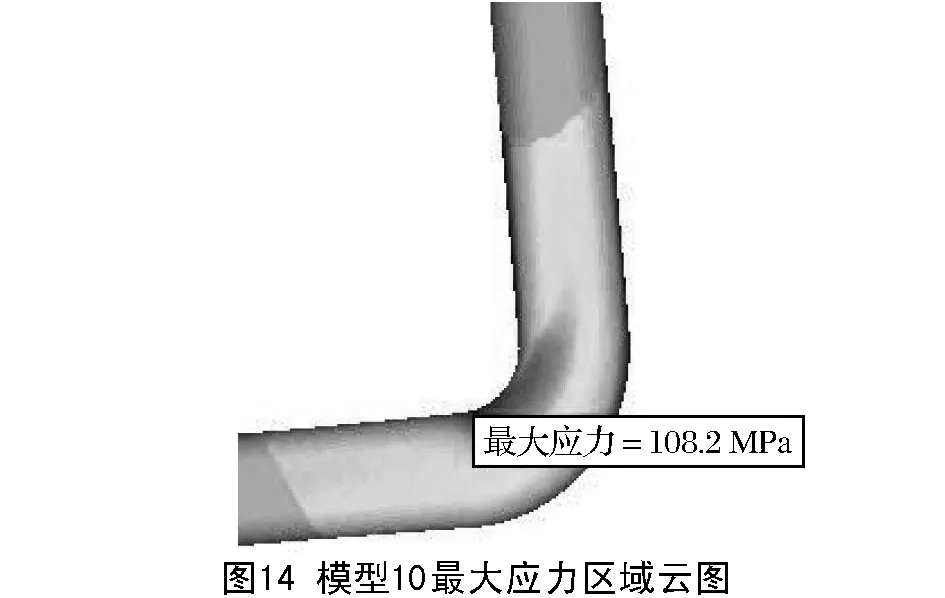


表2 各模型最大应力及变形结果
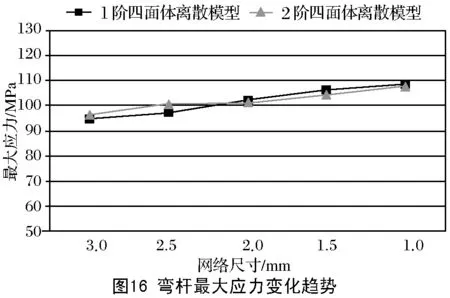
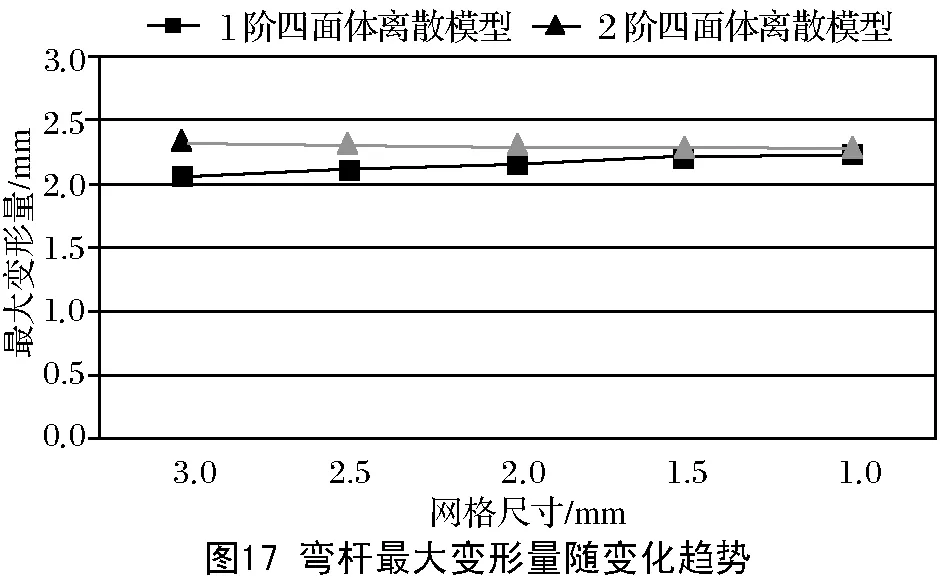
随着网格细化,各模型的最大应力及变形量变化趋势分别如图16和图17所示。相同网格尺寸下,1阶较2阶模型计算结果相对误差分析如表3和表4。
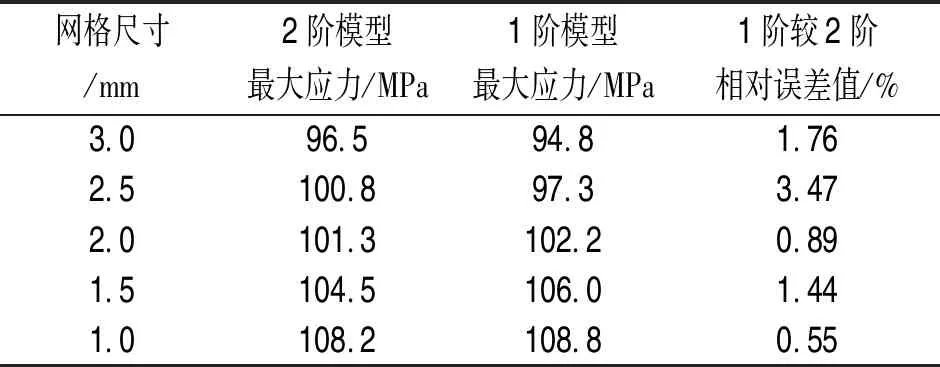
表3 最大应力相对误差分析
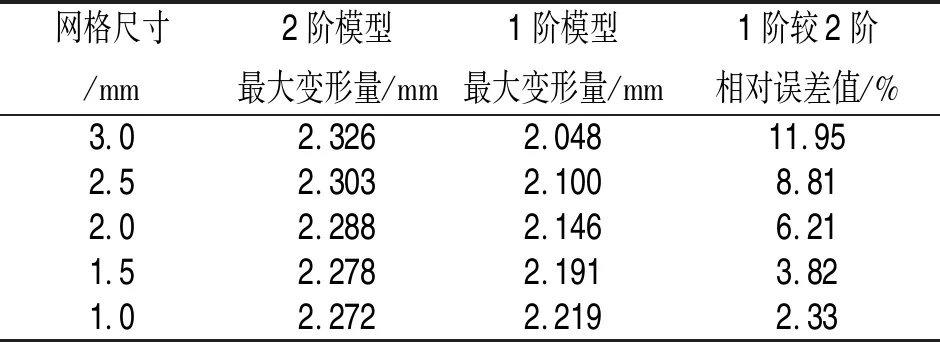
表4 最大变形量相对误差分析
3.2 结果分析
(1)应力分析
同一网格尺寸下,两种类型四面体单元离散模型的最大应力结果差别较小,但随着网格的细化,1阶与2阶模型的最大应力均呈现增大趋势,此时,网格细化对结构应力精度的提升贡献度较大。
(2)变形分析
网格细化,2阶模型的最大变形量结果较为稳定,而1阶模型在网格较粗时,计算结果较2阶模型差别较大,但随着网格的细化,相对误差减小,逐渐趋于2阶模型计算结果。即较粗的单元网格尺寸下,2阶模型能获得更高的分析精度。
根据有限元理论知,网格划分越细,单元阶次高,离散得到单元、节点越多,插值计算的精度也就越高,但是,计算规模的增加对计算机性能的要求越高,且耗费更多计算时间[7]。
因此,对于常规的小变形线性静态分析,在计算效率允许且精度没有特别要求的情况下,可选用低阶单元同时细化网格来分析计算,在精度要求较高的场合且计算效率允许的情况下,采用细化网格和增加阶次结合的方式能获得更高的计算精度。
4 结语
对产品结构进行有限元分析已经成为工程结构分析中的重要手段,本文借助CAE分析软件以L形套筒弯杆为例,选用低阶和高阶四面体单元并以不同网格尺寸进行结构离散,通过计算对比,探讨四面体网格阶次及细化对此结构静态分析结果的影响,可为工程CAE分析前处理中单元类型与尺寸的选用提供参考。
