面向移动机器人快速全局路径规划的改进跳点搜索算法
2020-11-24宋晓茹任怡悦
宋晓茹, 任怡悦
(1.西安工业大学电子信息工程学院, 西安 710021; 2.西安工业大学自主智能创新团队, 西安 710021)
路径规划是移动机器人实现自主化和智能化的关键技术,路径规划算法的性能直接影响移动机器人的工作效率,成为一个重要的研究领域[1-2]。栅格法因其便于机器人控制器存储、处理、更新和使用[3],常用于完成环境的构建和表示,基于此衍生出的全局路径规划算法有Dijkstra算法、A*算法、Swamps算法、SUB算法、跳点搜索算法等。
Dijkstra算法[4]是典型的最短路径算法,Chen等[5]基于Dijkstra算法建立了用于车辆疏散的动态道路网络模型,为公共场所的最优紧急疏散路径选择和应急救援决策提供了良好的方案;然而Dijkstra算法需要遍历大量节点,导致效率低下。针对此问题,Ren等[6]采用邻接列表和循环链表,进行权重排序得到改进的Dijkstra算法,用于解决最短路径的交通网络问题。A*算法[7]是一种求解最短路径最有效的直接搜索算法,针对其存在内存开销大,计算时间长等缺点,Korf[8]提出IDA*,融合了迭代加深算法于A*算法中,不需要进行状态判重和估价排序,减少空间需求;Botea等[9]提出HPA*,通过提高启发函数的准确度,减小搜索空间,提高效率,但空间复杂度高。Pochter等[10]提出Swamps算法,采用离线预计算的方式将网格地图分解为一系列相邻的区域,识别并忽略与最优解无关的无效区域,减少搜索时间与搜素节点。Uras等[11]提出SUB算法,通过预先将网格地图转换为可视化图(称为子目标图)来工作,然后算法存储和搜索的是子目标图,而不是原始的网格来寻找最优路径。
在栅格环境中,影响算法效率的最重要因素是存在大量对称性路径,将路径视为无序的向量而不是有序的节点序列时,可以看到地图中有许多路径共享相同的起点和终点,且能通过交换其中一条路径组成向量之间的顺序,得到另一条路径。这些大量对称性路径的存在导致算法需要去评估许多等效状态,阻止了向目标点的真正进展。然而上述研究均不是通过识别并消除对称性而得到最优路径。
Harabor[12]提出跳点搜索算法(jump point search,JPS),通过图裁剪来减少搜索过程的对称性,并在扩展节点的过程中筛选特定的节点——“跳点”,不仅提升了性能而且降低了内存成本。Jia等[13]在迷宫搜索方面对比了各算法的路径规划能力,比较了跳点搜索算法、A*算法与HPA*算法的搜索时间和效率,实验结果证明跳点搜索算法明显优于其他算法;赵晓等[14]结合跳点搜索算法改进A*算法,筛选出关键点进行扩展,加速全局路径规划的效率。但以上都只是简单的应用跳点搜索算法,并未对其进行改进。
跳点搜索法中识别关键跳点涉及了大量的迭代过程,成为了算法一个新的瓶颈,因此Harabor等[15]提出了JPS+算法,将栅格地图信息预处理为查询表,通过查找表格信息直接获得路径中的下一个跳转点,消除了跳点搜索算法引起的最大的处理开销。Traish等[16]提出了BL-JPS算法,通过预处理网格内障碍物边界和地图边缘位置来加速跳跃点的识别。但以上对跳点搜索算法的两种改进方式都是离线操作,通过预处理地图信息,大幅度提高搜索速度,当地图发生连续改变时,重新评估最佳路径过程中的任何开销都会成为实时路径规划的性能问题。
针对以上问题,采用“块”操作方法,在一次搜索中快速扫描底层网格中的一个区域,将跳点搜索算法中的修剪规则一次应用于多个节点,以达到快速识别跳点的目的,并对仅仅只具有改变方向性质的跳点进行剔除。此策略完全为在线方式,不需要任何特殊的数据结构,也不存储或计算任何其他信息,并同时保留了与原始算法相同的固有优势:完整性与最优性。为了验证算法的有效性与可行性,分别在规则的网格地图、测试库基准地图及移动机器人Turtlebot2进行对比实验。
1 跳点搜索算法(JPS)
跳点搜索算法的主要思想是对称修简规则和跳点识别规则,搜索过程会递归的调用这两种规则。优势在于考虑了与扩展节点相关的父节点位置,即每条规则都会根据上一步的方向(直行或沿对角线)来决定这一步应该朝什么方向前进,并为正在评估的节点标识一组“自然”邻居和“强制性”邻居。“自然”邻居由扩张方向定义:基本方向上(水平方向、竖直方向)的自然邻居定义为同一方向的下一个节点;对角线方向的自然邻居集包括3个节点:沿着对角线的下一个节点,以及下一个垂直和水平节点。规则的例外是扩展与障碍物相邻的节点,在这种情况下必须考虑无法直接从父节点访问的路径,识别强制性邻居。
1.1 修剪规则
识别出不需要被评估的节点,以便快速到达目标,具体通过比较两条路径的长度来完成。一条路径起始于p(x),经过节点x进行直线或对角线运动;另一条同样起始于p(x)进行直线或对角线运动,但是不经过节点x,如图1所示。其中经过节点x的路径明显更短且减少了对周围邻节点的重复访问,因此为了筛选跳点,需要删掉这些不必要的节点,即图中的灰色栅格。不论两条路径中任意一条所涉及的节点必须属于x的邻居集内。若邻居集内不包含障碍物,应用直线或对角线修剪之后的节点称为x的自然邻居,如图1中的白色栅格;当邻居集内包含障碍物时,这时评估的节点称为强制性节点,如图1中的斜杠栅格。
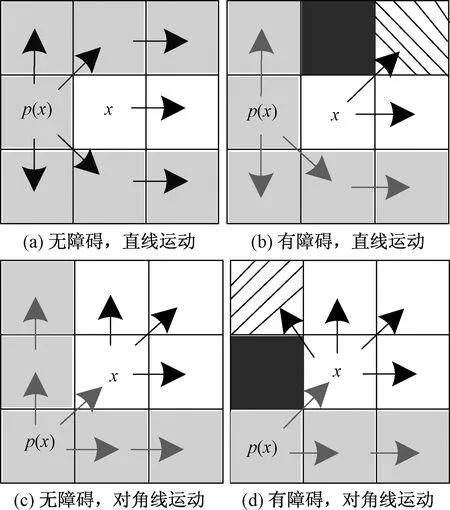
图1 修剪规则示意图Fig.1 Diagram of pruning rule
1.2 跳点识别规则
识别并选择性扩展某些特定的点,这些被选中的节点称之为跳点,用于加速寻找最优路径。两个跳点所连接路径上的中间节点不被扩展,直接从一个跳点移动到下一个跳点。跳点识别规则可归纳为y=x+kd,从x点出发,通过在d方向移动k步到达y,其中拥有最小k的节点y称为x的跳点。
(1)节点y目标点。
(2)节点y含有至少一个强制性节点。
(3)若d为对角线移动,存在z=y+kidi,其中kiN,z是y的跳点,则y也是x的跳点。
跳点识别规则示意图如图2所示。
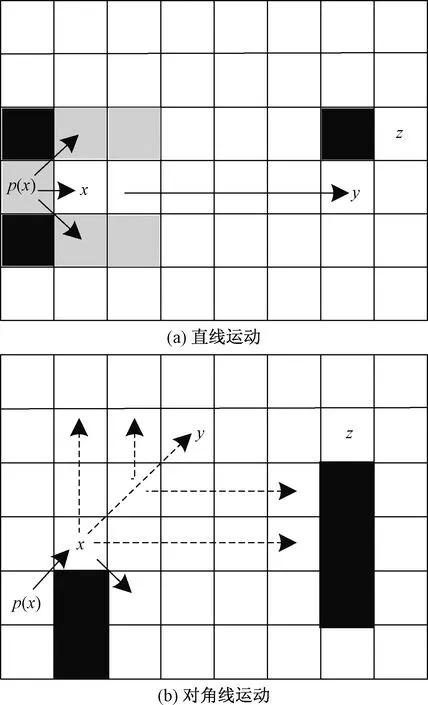
图2 跳点识别规则示意图Fig.2 Diagram of jump point identification
2 改进的跳点搜索算法
如何快速有效地发现跳点已成为跳点搜索算法的瓶颈问题。表1给出了在3种模拟真实环境的测试库基准地图上运行大量示例所获得的数据,可观察到跳点搜索算法需要花费约90%的时间用于生成后继者,A*算法花费约40%的时间,而在对Openlist和Closedlist列表中节点的操作约占10%,因此跳点搜索算法的效率取决于能否快速生成后继节点。

表1 3种模拟真实环境的基准地图上所占搜索时间比例的对比Table 1 Comparison of the proportion of search time on three benchmark maps that simulate real environments %
提出在一次搜索中快速扫描一个区域而不是单独的节点,将修剪规则一次应用于多个节点,节省大量且毫无意义的节点操作,以达到快速识别跳点的目的,并在采取对角优先的方式的前提下,剔除仅具有改变方向的中间转折点。当递归的应用这些规则时,可达到快速识别跳转点的目的,有效提升最优路径搜寻的效率,显著提高寻路搜索的整体性能。
2.1 基于“块”操作
跳点搜索法产生跳点的原因有3个:在当前行检测到死胡同、在相邻行找到强制邻居和检测到目标节点。首先针对死胡同的检测,将网格编码为位矩阵,其中一个位表示一个位置,记录障碍物信息,指示关联节点是否可遍历。当沿着固定的行或列递归搜索时,一次性读取固定设置好的32位输入,这32位的节点信息赋予算法“远眺”功能,快速检测出当前行是否为死胡同,并立即给出是否应当放弃对当前行的进一步操作的指令。
在算法第一次遇到死胡同之前,可能存在“直线-对角线”的转折点,即在邻行中出现强制性邻节点,这时需要综合当前行、当前行的上一行及下一行3行信息。若在上一行或下一行检测出前一位置存在障碍物而在当前位置没有障碍物,则在当前位置上存在潜在的强制邻居,如图3(a)所示。但算法也可能出现一直前跳的情况,以设置好的固定长度丈量地图,可实现对地图的快速遍历。
为了避免算法跳过目标节点,将目标位置、当前跳点与下一个跳点的连接,若此路径与目标位置所在的行或者列存在交集,则在交集位置添加一个中间节点。如图3(b)所示,当从N跳到S时,可看出路径穿过目标点所在的列,为避免跳过目标点T,在点T的列上插入一个中间后继点J。
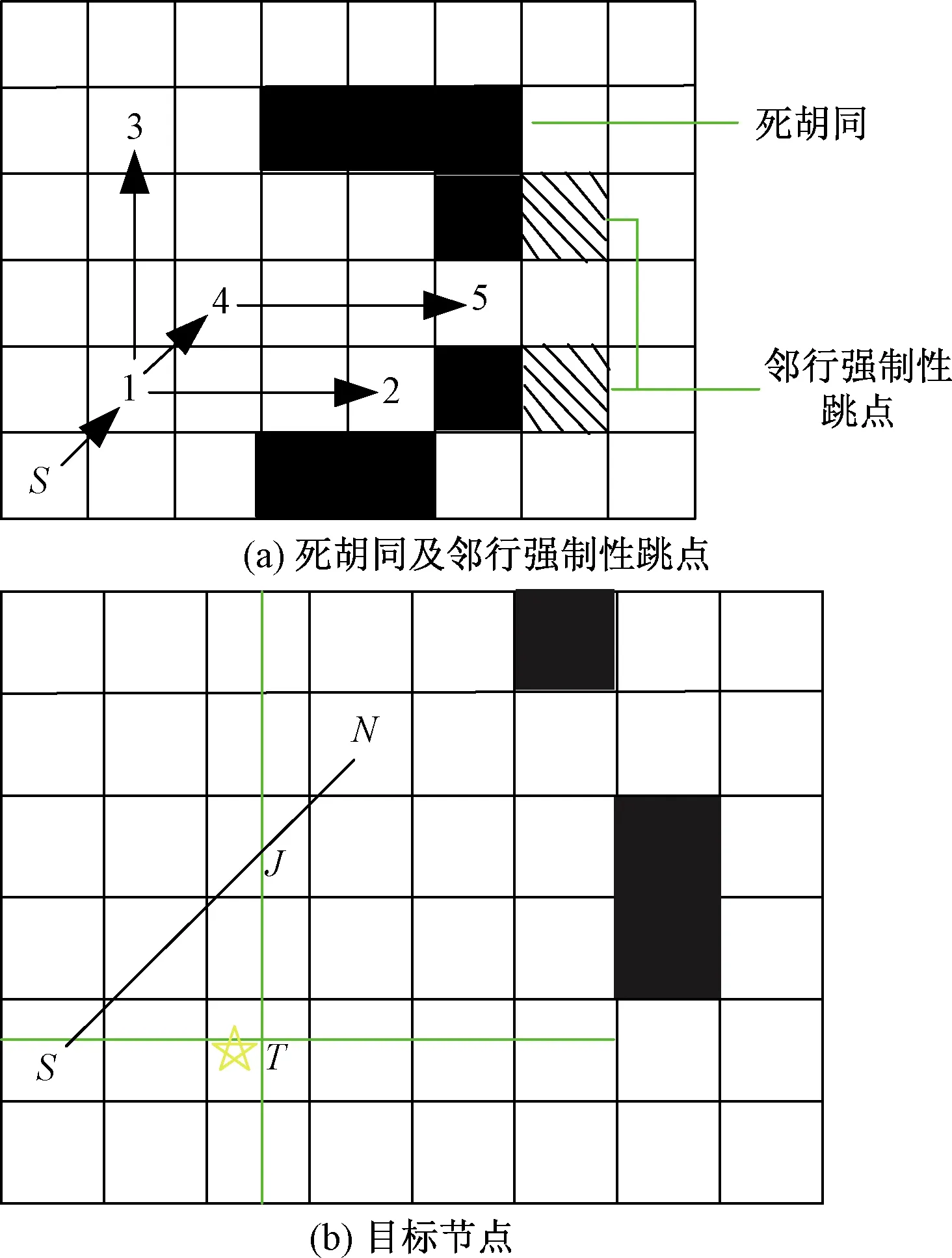
图3 基于“块”操作示例Fig.3 Example of “block” operation based
2.2 剔除中间转折点
路径中的转折点代表着路径方向发生了改变,即当nk-1到nk的行进方向与nk到nk+1的行进方向不同时,节点nk为转折点。最优路径π中转折点会有以下3种情况:对角线-对角线、直线-对角线、对角线-直线,如图4所示。
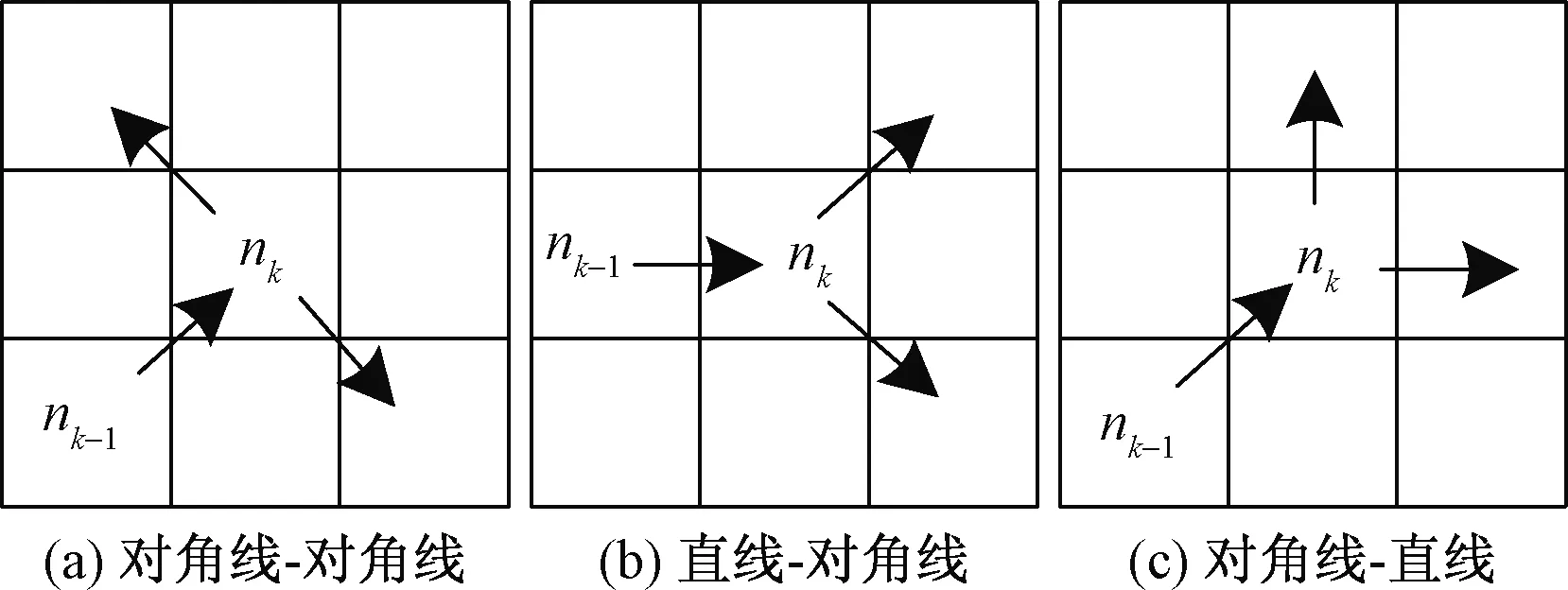
图4 最优路径的3种转折点Fig.4 Three turning points of the optimal path
对于这3种情况需要进一步区分至少有一个强制性邻居的转折点和没有强制性邻居的转折点,第1种类型至少紧邻一个障碍物,如果将其修剪就可能无法返回最优路径;第2种类型的跳点不紧邻障碍物,只是一个用来改变方向的中间节点。
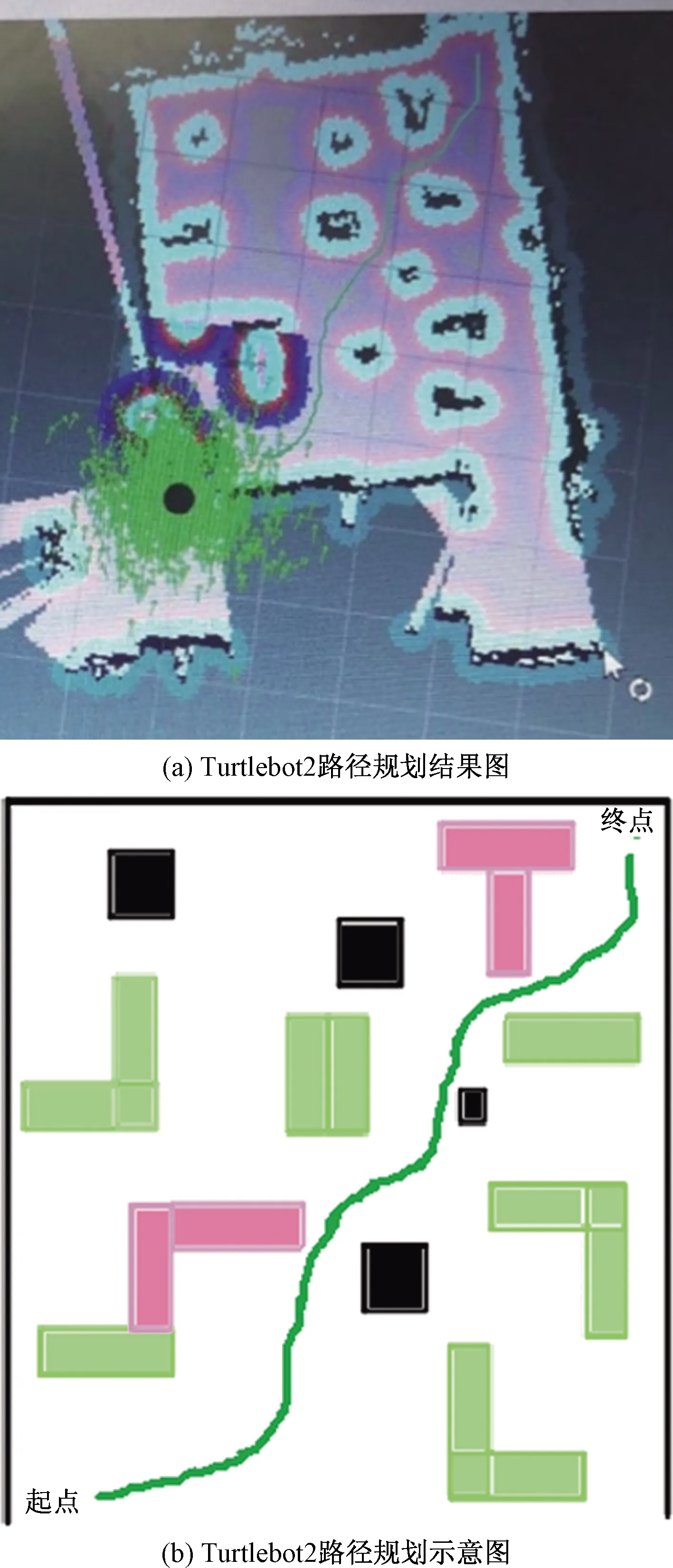
对以上3种情况进行分析,首先“对角线-对角线”转折点:因为π是最优的,所以在紧邻nk和nk-1的附近必然存在一个障碍物,强制路径绕行。若不存在障碍物,必然存在dist(nk-1,nk+1) 提出删除第2种类型的跳点,将其后继节点存储在列表中,并且每个新孤立的后继节点的父节点将成为开始跳转的起始位置,后继节点的g并没有因此而发生改变,在提取具体的路径时,以“对角优先”的方式从最后路径中的一个跳点移动到下一个跳点。此策略完全为在线方式,不需要任何特殊的数据结构,也不存储或计算任何其他信息。 为了验证本文算法的可行性和有效性,将本文算法与传统A*算法、JPS算法和JPS+算法进行对比,分析定性和定量结果。实验环境为规则的网格地图、测试库基准地图,计算机配置为Windows7,处理器为AMD A8-4500M,运行内存为4 GB。 在两种规格的网格地图中进行仿真,分别为13×19和30×60。图5所示为13×19网格地图下的仿真实验,障碍物随机生成,障碍物的平均密度设定约为20%。 绿色带圆圈栅格表示起始节点;红色带星星栅格为目标节点;灰色栅格表示寻路算法在搜索过程中访问过的节点;蓝色折线表示生成的最终路径。图5 A*、JPS及改进后的JPS网格地图仿真实验结果Fig.5 Grid map simulation experiment results of A*、JPS and improved JPS algorithm 从图5中可直观看出,A*搜索过的节点几乎覆盖所有网格,搜索量巨大,导致耗时长,实时性差;JPS减少了搜索的节点数量,在搜索过程中识别出跳点,然后直接从一个跳点移动到下一个跳点,并在对称性路径中进行对角优先选择;改进后的JPS进一步减少搜索的节点数量,并一次性读取固定长度的节点信息,快速识别出当前行是否存在死胡同,若为死胡同则快速舍弃对当前行的操作,并剔除了仅具有改变方向的中间转折点,加快关键跳点的搜寻。 表2所示为30×60网格环境下仿真实验的数据对比。分析表2数据得知,与传统A*算法相比,改进后的JPS扩展节点数目缩减了68.9%,搜索耗费时间降低了71.9%,与JPS相比,扩展节点数目缩减了41.3%,搜索耗费时间降低了33.4%。主要在于改进后的JPS通过“块”操作提高了节点数目查询的效率,剔除中间转折点缩减了扩展节点数目,使得最终在返回同等长度最优路径的前提下,搜索耗费时间下降。 表2 30×60栅格环境下数据对比Table 2 Data comparison in 30×60 grid environment 实验地图采用基于网格路径规划竞赛(grid-based path planning competition,GPPC)[17]中的基准库地图,该比赛旨在提供一套标准的地图,对算法性能进行有意义的比较,已得到IBM Research,University of New South Wales等研究机构的广泛认可,地图集可从比赛官网上直接获得。实验选用Rooms、Dragon Age Origins及Adaptive depth三类地图,如图6、表3所示。 表3 基准库地图Table 3 Benchmark sets 为了进行有说服力的算法验证,将改进后的JPS算法与JPS、JPS+算法进行性能比较,评估了搜索时间和路径长度。在搜索的过程中重复生成起点到终点之间的最优路径,最优路径上每相邻的两点搜寻时间至少计算100次,直到这两点间最优路径运行时间累加到至少需要5 ms,然后最优路径平均搜索时间为总时间除以总迭代次数。 JPS+将栅格地图信息预处理为查询表,通过查找表格直接获得路径中的下一个跳转点,提出的改进算法是通过“块”操作方法获得路径中的跳点,相较于JPS,以上两者一个是通过预处理来获得更快的搜索速度,一个是一次性将修剪规则用于获得更多的节点信息来加快运行速度。JPS、JPS+与本文算法三者所使用的修剪规则与跳点识别规则是一致的,虽然本文算法剔除了仅具有改变方向的中间转折点,但保留了后继点在列表中,这步操作只是减少了扩展节点数目,是加快搜索速度的一部分,所以在每幅测试地图中3种算法返回的最优路径的长度是一致的。 抽取实验中部分数据如图7所示。图7中横坐标表示测试的每幅地图中最优路径长度,纵坐标表示所耗费的搜索时间,可看出在每幅地图中,JPS+都快于在线搜索的JPS和改进的JPS,但本文算法也大幅度提高了搜索速度,且是完全在线的,不需要任何特殊的数据结构,也不存储或计算任何其他信息,充分表明了本文算法的优越性。 图7 基准库地图下3种算法时间对比Fig.7 Time comparison of three algorithms under the benchmark sets 为了验证改进算法在实际应用中的可行性,在基于机器人操作系统(robot operating system, ROS)的移动机器人Turtlebot2进行真实场景下的实验,计算机为华硕笔记本(i5-5200),系统为Ubuntu14.04+ROS Indigo版本。该机器人基于差速两轮驱动,配备了由微软开发的Kinect深度传感器作为视觉传感器,韩国的Yujin Kobuki作为移动基座,如图8所示。 图8 TurtleBot 2移动机器人Fig.8 TurtleBot 2 mobile robot 实验场景为5 m×3 m,障碍物随机放置,占有率为20%。首先,3D体感相机Kinect获取外界环境信息,然后调用Gmapping模块的数据创建地图,初始扫描设置为20 cm/s的前进速度和20 cm/s的旋转速度,确保机器人可充分分析环境数据并建立环境地图,如图9所示,其中黑色部分被认为是检测和识别后的障碍物。 图9 实验场景与SLAM构建的环境地图Fig.9 Experimental scene and environment map constructed by SLAM 在上述SLAM构建的环境地图中进行改进JPS算法的实验验证,起点选择为SLAM地图的原点,即建图的起始位置,目标点选为起始点的对角位置,amcl模块完成机器人自定位,move_base模块调用改进后的JPS算法,驱动和控制机器人移动到选定的目标,在rviz可视化界面中,点击2Dpose Esitimate选取地图中机器人初始位姿,2DNavGoal给定小车在地图中的目标位置,绿线为机器人规划出的路径,实验过程如图10所示,实验结果如图11所示。 图10 改进的JPS Turtlebot2路径规划过程Fig.10 Path planning process of improved JPS on Turtlebot2 图11 改进的JPS Turtlebot2路径规划结果图及示意图Fig.11 Path planning real result of improved JPS on Turtlebot2 and diagrammatic drawing 针对JPS搜寻跳点时所涉及大量迭代产生的过大计算量,提出通过“块”操作方法,在一次搜索中快速扫描底层网格中的一个区域,将JPS中的修剪规则一次应用于多个节点,并在采取对角优先方式的前提下,剔除仅具有改变方向的中间转折点,提高了单个节点的平均处理时间,达到了快速识别跳转点的目的,同时保留了与原始算法相同的固有优势:完整性、最优性。最终实验结果表明了本文方法的优越性。下一步计划利用歧路检测和状态空间的剪枝算法,如Dead-end heuristic,Swamps或者Portal heuristic算法,在搜索过程中通过识别并忽略无需探测的区域来最优化地到达目标点。3 仿真实验验证及结果分析
3.1 网格地图仿真实验
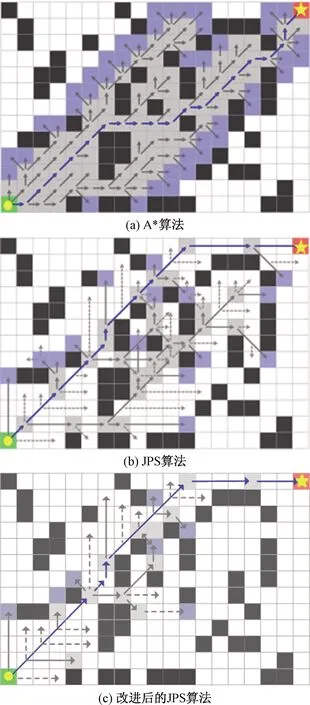
3.2 基准库地图仿真实验

4 实验验证及结果分析


5 结论
