基于马尔科夫优化的灰色GM (1,1) 沉降预测模型及应用

翁志坚， 邱晨杰， 邱福祥， 杨芸红， 卢如发， 何生龙

(中铁二十四局集团福建铁路建设有限公司， 福州 352000)

目前城市建设过程中对于地下空间的利用和开发越来越重视，随之带来的各种复杂条件下大型深基坑工程问题也越来越多。随着城市深基坑工程规模越来越大，且周边环境越来越复杂，开挖过程中深基坑工程的安全问题也引起了学者们的广泛关注。沉降变形观测是基坑施工过程中的重要环节[1]，通过对施工过程中基坑支护结构的变形及地表、周边的沉降进行实时监测，可以有效及时地发现问题，从而保证基坑工程施工的安全进行。中外许多学者对沉降预测方法进行了研究，目前常用的有双曲线法[2]、Asaoka法[3]、神经网络法[4-5]、灰色理论法[6-8]等，其中灰色理论法由于只需较少的数据样本即可对沉降进行有效的预测，因此在沉降变形预测中得到了较为广泛应用。李小刚等[9]采用灰色GM(1,1)模型对某道路地基沉降过程进行预测，并将预测结果与规范中的双曲线法、三点法预测结果进行了对比分析，结果表明灰色GM(1,1)模型的预测精度更高。刘寒冰等[10]在灰色GM(1,1)模型的基础上，提出了考虑多监测点间相关性的多变量MGM(1，n)灰色模型。张闯等[11]、傅家俊等[12]在传统灰色Verhulst模型的基础上，提出采用离散化方法对原始数据列进行倒数变换，由此建立了优化的灰色Verhulst模型，通过工程实例验证了优化后的模型较传统灰色Verhulst模型具有更好的预测精度。何亚伯等[13]、唐葭等[14]针对实际工程中非等间距的观测数据，分别提出采用3次样条插值法和最小二乘法对原始数据的非等距关系进行处理，随后采用处理后的数据进行GM(1,1)模型建模分析，由此建立了非等距时间序列模型，并采用该模型分别对隧道拱顶位移和路基沉降进行预测分析。

实际工程中由于监测数据受到外界各种因素的影响，其往往具有较大的波动性，而灰色理论法对波动较大的数据进行预测时会存在一定的误差。马尔科夫链(Markov chain)理论能较好地描述预测对象随机的动态变化过程，通过对研究各状态间的转移概率来对预测对象下一步的状态进行预测，目前该理论已在公共交通和沉降变形分析等领域中得到广泛应用[15-16]。现在灰色GM(1,1)模型的基础上，结合马尔科夫链理论，提出基于马尔科夫优化的新维GM(1,1)沉降预测模型，并结合福州市火车北站南广场深基坑工程施工过程的周边地表沉降观测数据，对本文模型的合理性和准确性进行验证。研究结果可为相关城市深基坑工程的沉降变形预测提供参考。

1 灰色GM(1,1)模型

灰色GM(1,1)模型是灰色系统理论中应用最为广泛的模型，该模型的基本思想是首先对原始数据进行一次累加，采用累加后的数据列进行建模计算，最后将模型计算值进行累减后即可得到预测值。具体步骤如下。

设有原始非负数据列为

X(0)={x(0)(1),x(0)(2),…,x(0)(n)}

(1)

将原始数据列进行一次累加处理，得到累加后的数据列为

X(1)={x(1)(1),x(1)(2),…,x(1)(n)}

(2)

灰色GM(1,1)模型的白化微分方程为

(3)

式(3)中：a、b为参数。

通过对方程进行离散化，得到灰色GM(1,1)模型为

X(0)(k)+aZ(1)(k)=b

(4)

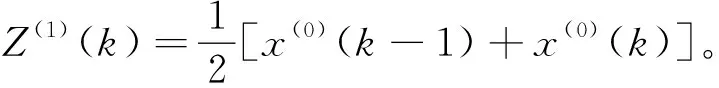
参数a、b可采用最小二乘法进行确定，即

(5)

式(5)中：

(6)

(7)

根据式(5)求得参数a、b后，将其代入式(4)中即可得到模型的时间响应函数为

(8)

将式(8)计算得到的结果通过累减，即可求得模型的预测值为

(9)

2 新维GM(1,1)模型

基坑沉降监测过程中，随着监测的进行会不断有新的观测数据补充进来。在对基坑沉降进行预测时，初期的旧数据将对预测结果的影响越来越小，而新的观测数据更能体现基坑沉降的发展趋势，即实测沉降数据具有明显的时效性。曹文贵等[17]也指出，实测数据的新旧程度对沉降预测的效果具有显著的影响，距离预测时间点越接近的实测数据对沉降预测的影响越大。为了更准确地对基坑沉降变形进行预测，需要不断更新观测数据且将旧数据剔除，才能提高模型预测的精确度。为此，基于新陈代谢的思想，建立了新维GM(1,1)模型，其具体步骤为：使用n维的原始数据列进行初始GM(1,1)模型建模，并对第n+1时序的沉降进行预测；在获得第n+1时序的实测值后，将第一个实测值进行剔除，并将第n+1时序的实测值添加到数据列中，实现原始数据列的等维。采用更新后的数据列再次进行GM(1,1)建模，并对下一步的沉降进行预测，由此实现对基坑沉降的滚动预测，直至完成预测目标为止。

3 基于Markov优化的GM(1,1)模型

由式(8)可知，灰色GM(1,1)模型对于符合指数发展规律的沉降曲线具有较好的适应性，而实际工程中基坑沉降变形存在一定的波动，因此采用该模型对基坑沉降变形进行预测时仍存在一定的误差。马尔科夫链理论描述的是状态空间中从一个状态到另一个状态转变的随机过程，在对基坑沉降变形进行预测分析时，将灰色GM(1,1)模型预测值与实际沉降之间的相对误差序列认为是一个随机过程，通过马尔科夫链对相对误差进行修正，进而对灰色GM(1,1)模型的预测值进行修正。基于马尔科夫优化的灰色GM(1,1)模型实现了二者的优势互补，对随机波动较大的沉降变形过程能进行更为准确地预测。基于马尔科夫链理论的优化步骤具体如下。

首先计算灰色GM(1,1)模型预测的相对误差ε，即

(10)

根据相对误差序列的分布范围，将其分为n个状态区间，第i个状态区间记为Si(i=1,2,…,n)，对应的状态区间范围为[Q1i,Q2i]，根据相对误差序列与状态空间关系，确定状态转移概率矩阵P为

(11)

式(11)中:pij表示由状态Si转移到状态Sj的概率，其计算公式为

(12)

式(12)中：Ni为状态Si出现的次数；Nij为状态Si转移到Sj的次数。

状态转移矩阵P表示的是系统中各状态转移到下一状态的概率。假设初始状态向量为ε0，则在经过n步转移后的状态向量εn为

εn=ε0Pn

(13)

根据状态向量εn即可确定n步转移后相对误差最有可能处于的状态区间。通常在实际预测时只考虑一步转移的情况，即式中n=1；若当前状态处于Sm状态，则只需考虑转移矩阵P中的第m行，若max{Pmj}=Pmk，则下一步预测对象最有可能从Sm状态转向Sk状态，在确定下一步预测对象所处的状态区间后，即可得到修正后的沉降预测结果，即

(14)

(15)

4 工程实例分析

福州火车北站南广场综合改造工程西楼位于福州市晋安区站前路与站西路路口北侧，拟建建筑物最大标高约为100 m，地下3层。西楼基坑工程支撑体系为止水帷幕+支护桩+两道混凝土内支撑，基坑北、西、南三面均设有止水帷幕，东侧因毗邻地铁外墙未设止水帷幕，支护桩桩间止水为桩径为800 mm的高压旋喷桩。该工程周边道路交错，道路两侧多分布有地下电缆、煤气管道、污水管、给排水管等各种类型的地下管线；且周边建筑以老旧多层住宅为主，工程北侧支护桩与既有东浦花园居民小区距离仅15 m，局部坑中坑开挖深度至17.9 m，属于超过一定规模的危险性较大的分部分项工程，因此在基坑开挖过程中必须对周边建筑物地表沉降进行实时监测，从而保证施工过程中基坑的安全和稳定。

为了验证前文中所提出的沉降预测模型的合理性，并对不同模型的预测效果进行对比，选取基坑周边建筑物沉降观测数据进行分析，该基坑工程共布置监测点19个，编号分别为M1～M19，采用其中监测点M4累计11个月的原始观测数据进行建模，并对基坑周边建筑物沉降变形进行预测分析，原始监测数据如表1所示。

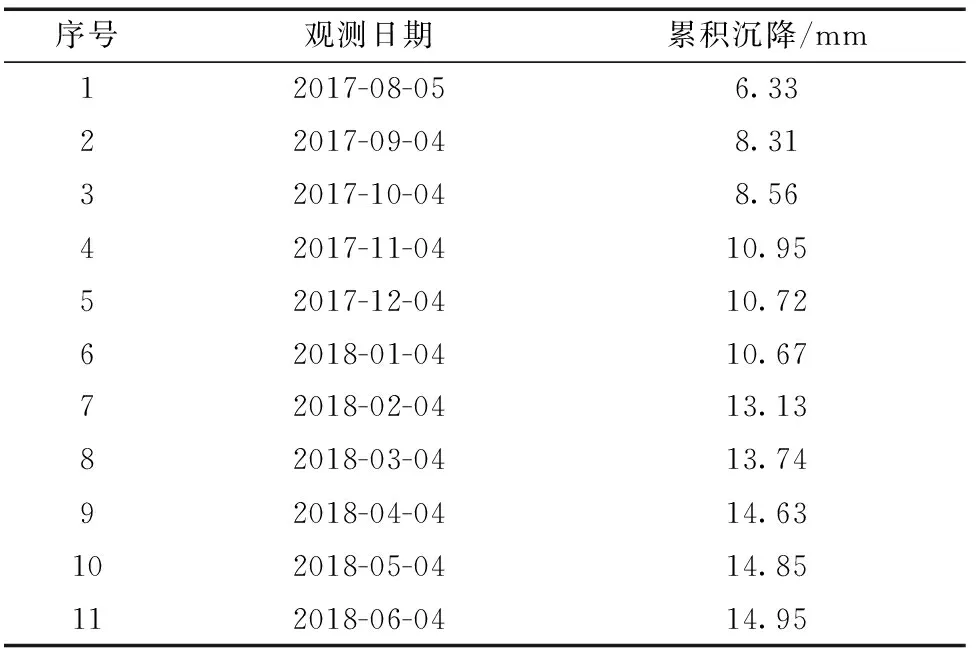
表1 M4监测点实测沉降Table 1 Settlement datas of M4 monitoring point

选取表1中前8个月的沉降监测数据进行GM(1,1)建模，根据第2节中的步骤得到GM(1,1)模型参数a=-0.083，b=7.484 6。将参数a、b代入式(8)中，得到模型预测公式为

(16)

为了建立新维GM(1,1)预测模型，将新近的监测数据补充到原始数据列中，同时将原数据列中旧的观测数据剔除。具体步骤为将第1个月的观测数据剔除，使用第2—9月的观测数据作为原始数据列重新进行GM(1,1)模型建模，从而对第10月的沉降进行预测。同样根据步骤得到新维GM(1,1)模型中参数a=-0.079 6，b=8.131 7。将参数a、b代入式(8)中，得到模型预测公式为

(17)

同理，对第11月的累积沉降进行预测时，使用第3—10月的观测数据作为原始数据列重新进行GM(1,1)模型建模，得到模型参数a=-0.064、b=9.495。将参数a、b代入式(8)中，得到模型预测公式为

(18)

在采用马尔科夫链理论对GM(1,1)模型进行优化时，需要首先计算出GM(1,1)模型预测的相对误差，如表2所示。由表2可知，模型预测的相对误差范围为-9.96%～9.07%，因此分别以-10%、-5%、0、5%、10%为阈值，将其划分为S1、S2、S3、S4共4个状态区间，各状态区间范围分别为[-10%，-5%)，[-5%，0)，[0，5%)，[5%，10%)。由此可确定GM(1,1)模型预测相对误差所处的状态区间。

根据表2中各状态间的转换关系，采用第3节中步骤即可确定状态转移矩阵P。首先根据表2中状态区间的分布情况确定各状态出现的次数以及各状态间转移的次数，如表3所示；由于表2中最后一个时序的后续状态未知，即无法确定其向任一状态的转移概率，因此最后一个时序所处的状态区间不参与统计。

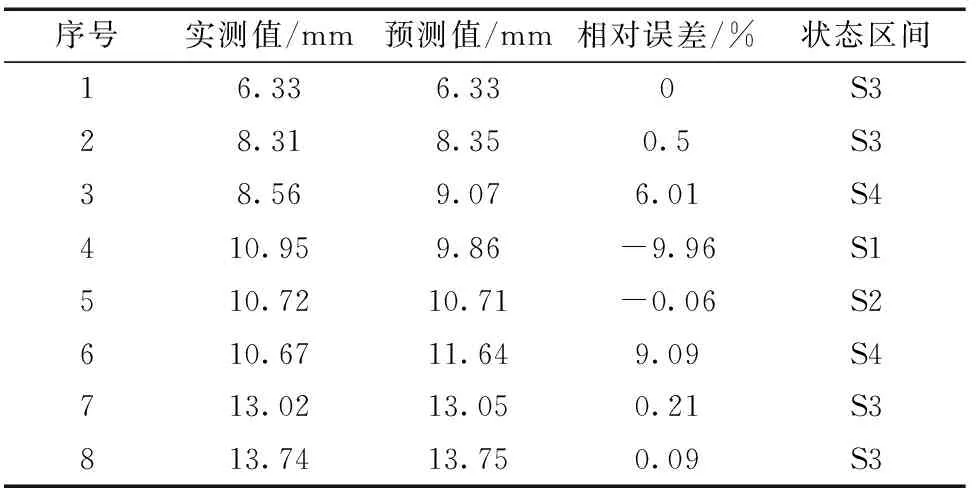
表2 GM(1,1)模型预测值与实测值对比Table 2 Comparison between measured value and predicted value by GM(1,1)model

根据表3的统计结果，采用式(12)计算各状态转移概率，最终确定状态转移矩阵P为

表3 马尔科夫状态转移统计结果Table 3 Statistical results of Markov state transition

(19)

根据马尔科夫链模型，第n步的状态概率向量εn可由式(13)进行计算。由于第8月时处于S3状态，因此确定初始状态概率向量ε0为

(20)

将初始状态向量代入式(13)中，可计算得到一步转移后的状态概率向量ε1为

(21)

由此可以得出第9月模型预测的相对误差最大可能处于S3状态，此时采用式(14)对预测结果进行修正。由GM(1,1)模型可计算得出第9个月沉降预测值为14.95 mm，基于马尔科夫链理论的修正预测结果为

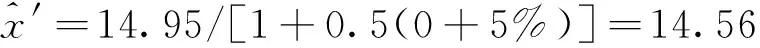
(22)

采用马尔科夫理论对新维GM(1,1)模型预测结果进行优化时，只需根据上述步骤对新维GM(1,1)模型预测的相对误差不断进行修正即可。如对第10月的沉降进行预测时，首先采用2～8个月的数据进行GM(1,1)建模，并根据模型预测相对误差的分布范围重新进行状态区间划分，确定状态转移矩阵P。根据上述步骤计算得到基于马尔科夫优化的新维GM(1,1)模型的预测结果。不同模型预测结果如表4所示。

从表4中可以看出，在对监测点M4的沉降变形进行预测时，传统GM(1,1)模型预测的平均相对误差为9.74%；新维GM(1,1)模型预测的平均相对误差为6.08%，表明考虑监测数据时效性的新维GM(1,1)模型能更为准确地对基坑沉降进行预测；而基于马尔科夫优化的新维GM(1,1)模型的平均相对误差最小，仅为1.64%，与GM(1,1)模型和新维GM(1,1)模型相比，基于马尔科夫优化的GM(1,1)模型的预测值与实测值最为接近。由此可见，基于马尔科夫链理论的优化方法能很好地弥补传统GM(1,1)模型的缺陷，从而明显地提高模型的预测精度。

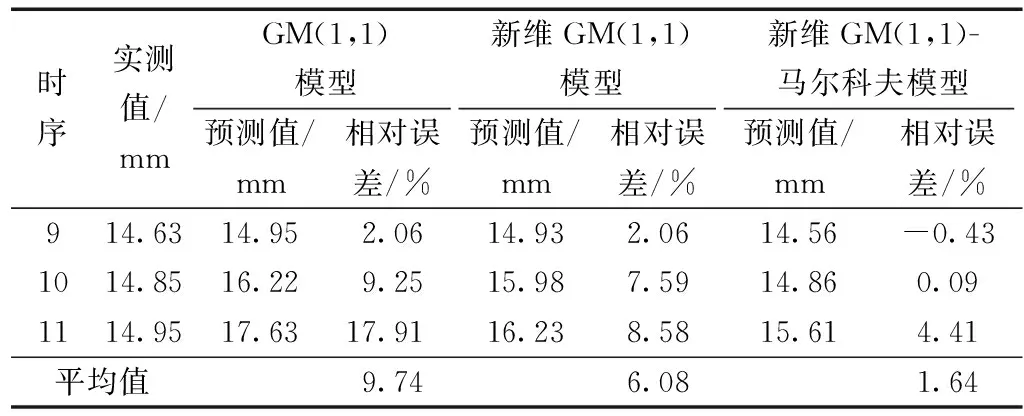
表4 不同预测模型预测结果对比Table 4 Comparison of prediction results by different models

5 结论

(1)考虑监测数据的时效性对GM(1,1)模型预测结果的影响，基于新陈代谢的思想，通过对原始沉降数据列中的观测数据进行不断更新，建立了新维GM(1,1)预测模型。

(2)采用马尔科夫链理论对GM(1,1)模型进行优化，根据GM(1,1)模型预测时所产生的相对误差的范围，对其所处的状态区间进行合理划分，并确定了对应的状态转移概率矩阵，由此建立了基于马尔科夫优化的GM(1,1)模型。

(3)通过工程实例对3种沉降预测模型的预测效果进行分析，结果表明：与传统GM(1,1)模型相比，新维GM(1,1)模型和基于马尔科夫优化的GM(1,1)模型预测的平均相对误差均明显降低，其中基于马尔科夫优化的GM(1,1)模型的平均相对误差最小，表明基于马尔科夫链理论的优化方法能明显地提高GM(1,1)模型的预测精度。