基于时变O-U均值回复模型的天气衍生品定价研究
2020-11-23唐欣邹楚瑜
唐欣 邹楚瑜

[摘要]馬铃薯作为我国主要的粮食作物,其产量受天气状况的影响较大。河北省张北、围场和丰宁三地是马铃薯种植最集中的区域,异常的天气波动会给当地农户带来严重的经济损失。天气衍生品可以帮助农户对冲农作物面临的天气风险,但要达到良好的风险对冲效果,就需要更加精准的定价模型。本文致力于寻求精度更高的定价模型,于是在传统的Ornstein-Uhlenbeck均值回复模型的基础上,引入时间序列模型来重新模拟均值回复速度,得到时变均值回复模型。之后,使用张北、围场、丰宁三地1951—2018年的日平均气温数据拟合2019年每日平均气温的动态变动过程,并检验模型预测精准度。最后,在此基础上,借助蒙特卡罗模拟法测算马铃薯生长温度指数期货合约的价格,并与传统的均值回复模型的定价结果做比较。研究表明,时变Ornstein-Uhlenbeck均值回复模型能够较好地拟合气温的变动趋势,并且比传统的Ornstein-Uhlenbeck均值回复模型更能精准地预测期货价格。
[关键词]天气衍生品;时变O-U均值回复模型;均值回复速度;生长温度指数
中图分类号:F842.66 文献标识码:A DOI:10.16465/j.gste.cn431252ts.202008
中国是马铃薯生产第一大国,而河北省的张北、围场和丰宁又是我国重要的种薯繁育、商品薯生产加工以及储运基地,具有十分重要的战略地位。马铃薯产业的发展对河北省农民精准脱贫、增收及粮食安全生产具有重要意义。而天气状况日益多变,可能会导致马铃薯减产,最终会波及整条马铃薯产业链,影响农户福祉。我国现有的政府补贴和农产品保险无法完全弥补天气风险管理的缺口,因此需要开发新型的天气风险管理工具,天气衍生品就是其中之一。天气衍生品诞生于1996年,是以天气指数作为标的资产的金融衍生工具,用以对冲天气反常变化带来的收入不确定性,这类产品在国外被广泛运用于天气敏感性行业的风险管理策略,其中就包括农业领域。但在我国,天气衍生品领域还是一片空白。
1 文献综述
在天气衍生品领域的研究中,普遍采用时间序列模型、Ornstein-Uhlenbeck均值回复模型(以下简称O-U均值回复模型)以及神经网络模型作为气温预测模型。研究思路大致分为三种,一是基于时间序列模型,如利用ARIMA模型、AR-GARCH模型对每日平均气温时间序列进行分析和预测;二是基于O-U均值回复模型,假设气温变量服从随机布朗运动,并利用蒙特卡罗仿真模拟来对天气衍生品进行定价;三是利用小波分析对气温序列进行分解和重构,并结合神经网络技术进行预测,以此来为天气衍生品定价。
国外学界对O-U均值回复模型的研究由来已久。Vasicek O[1]于1977年率先提出了利率变动的O-U均值回复模型,他认为利率的变化虽然是随机的,但是长期利率倾向于回归长期均值水平。O-U均值回复模型被运用于气温预测始于1998年,Dischel B[2]提出基于随机微分方程(SDE)的气温预测模型,并首次建立了平均气温的均值回复模型。而后,众多学者对Dischel提出的均值回复模型进行了实证检验和改进。Dornier F等[3]使用这一模型进行平均气温的预测,值得一提的是,他们将气温的波动率考虑为一个常数。Alaton P等[4]于2002年用一个正弦函数来描述温度的季节性变动,将温度的波动率考虑为按月变化的常数,提出了基于月波动率的O-U均值回复模型,并以此模型结合蒙特卡罗模拟对气温期权进行定价分析,得到了较好的实证效果。2003年Bhowan A[5]通过进一步的研究发现,气温的波动率并非按月变化的常数,其变化规律同样呈现出均值回复的特性。Benth F E等[6]在此基础上将温度的波动率考虑为日波动率,并对气温的季节项进行傅里叶变换,用多个正弦和余弦函数来描述气温的季节性变化,进而提出了基于日波动率的O-U均值回复模型,该模型成为运用最为普遍的气温预测模型。
而国内学界关于O-U均值回复模型对天气衍生品定价方面的研究不够深入,但起步其实并不晚。2006年刘国光[7]通过Alaton提出的基于月波动率的O-U均值回复模型,结合1980—1999年的北京每日平均气温数据进行模型参数估计,并运用蒙特卡罗仿真模拟法为天气期权和天气互换定价,实验效果较好。然而一直到2011年,国内学者才开始在刘国光的基础上进行改进。李永等[8]在2011年以O-U均值回复模型为基础,通过回归分析和傅里叶变换求得相关参数,并对上海地区1951—2008年的气温进行研究,发现预测值的相对误差绝对值均小于5%。2012年李永等[9]又以上海气温为例利用带Levy过程的O-U均值回复模型对天气衍生品定价的合理性进行测度,较好地模拟了气温的变化。此外,部分国内学者对传统的O-U均值回复模型还贡献了全新的研究思路,他们将均值回复速度设置为以年为单位的分段函数,由于每年的均值回复速度存在一定的差异,故将模型命名为时变O-U均值回复模型。其中最具代表性的研究是陈百硕等[10]在2014年和王明亮等[11]于2015年发布的两篇文献,均证明这种时变模型可以更好地拟合气温变动过程。本文也将延用这种方法进行实证分析。
2 时变均值回复模型和气温指数模型的建立
2.1 时变均值回复模型
2.1.1 模型的建立
3 实证与结果分析
3.1 基于时变O-U均值回复模型的气温预测
3.1.1 数据说明
本文选取了河北省三个主要的马铃薯产地张北、围场、丰宁1960年1月1日至2019年12月31日的日平均气温数据作为实验样本(单位℃,精确到0.1℃,共60年,去除闰年2月29日以后共计65 700个数据)。
3.1.2 气温时间序列的参数估计
由公式(5),对三个城市的日平均气温序列进行线性和非线性回归分析,在各参数均通过显著性检验的前提下,得到各自的气温长期趋势St:
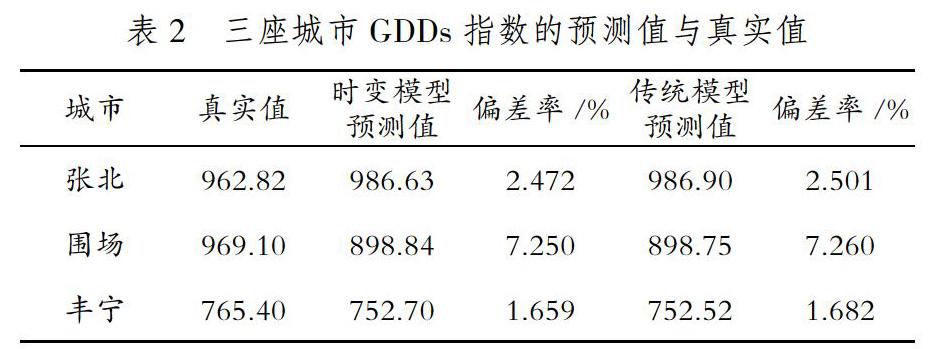
由公式(7),结合三座城市的日平均气温得到各自的月波动率值,将每日平均气温数据代入公式(11)可得均值回复速度,具体变动情况如图1所示。
由图1可知,三个城市的均值回复速度差异较大,且不存在明显的相关关系,需要继续讨论。
3.1.3 均值回复速度Ai的时间序列分析
三个城市Ai值的时间序列全部通过ADF单位根检验,观察自相关和偏自相关图判断出三个序列均存在序列相关问题。在引入ARIMA(1,0,1)后,序列相关问题得以解决,各系数也通过了显著性检验,模型的拟合效果很好。于是分别构建张北、围场、丰宁ARIMA(1,0,1)模型:
3.2 天气衍生品的设计与定价
3.2.1 标的指数的计算
本文选择基于马铃薯的GDDs指数期货定价。由于马铃薯的种植期多集中于第四季度,因此选取7.22℃作为马铃薯GDDs指数的基线温度,对预测得到的气温数据进行转化,得到三个城市2019年10月—12月(第四季度)分别的生长温度指数GDDs,通过与2019年实际的GDDs指数做对比,来判断时变O-U均值回复模型的预测精度,结果如表2所示。
由此可见,三座城市的GDDs指数的预测值和真实值之间的偏差率均不超过8%,说明两种预测精度较好,并且时变O-U均值回复模型的预测精度要比传统的O-U均值回复模型更高,能够更好地拟合气温变动情况。
3.2.2 天气衍生品的设计与定价
本文为张北、围场和丰宁分别设计一份天气衍生品期货合约。按照芝加哥商品交易所(CME)对天气指数期货合约的规定,合约规格设置如表3所示。
结合公式(13)将GDDs指数转化为合约价格。假设买方分别在10月1日、11月1日、12月1日进入期货多头或空头,分别计算三个时点的期货价格,比较两种模型预测的合约价格与真实价格的偏差程度,判断时变O-U均值回复模型的改进效果。由于篇幅原因只以丰宁为例进行展示,如表4所示。
由表4可知,当以丰宁为标的城市时,两种O-U均值回复模型都能较好地贴近期货的价格,预测的偏差率均小于5%,且时变模型效果更佳。其他两座城市以两种模型进行实证分析的效果均较好,大部分预测偏差率小于8%(个别值除外),并且时变模型整体效果要优于传统模型,虽然精度提升的幅度不大(平均提高0.2%左右),但是由于交易体量较为庞大,依旧能明显改善期货的作用效果。此外,两种模型模拟不同城市的期货价格的效果不同,其中对丰宁的期货价格的预测效果最佳(平均误差率不超过3%)。
4 结论与展望
本文着眼于提高传统的天气衍生品定价模型——O-U均值回复模型的预测精准度,将均值回复速度从常数改进为ARIMA时间序列,构建时变O-U均值回复模型。以河北省张北、围场和丰宁三个马铃薯种植大县为例,选取1960—2019年的日平均气温数据,对时变O-U均值回复模型的预测精确度进行了实证分析。之后,基于马铃薯的生长温度指数GDDs设计天气期货产品,利用蒙特卡罗模拟法拟合了期货合约的价格,并与传统的O-U均值回复模型的拟合结果做比较分析,考察两个模型的效果差异。研究发现,三个城市的均值回复速度变动趋势各不相同,但均适合引入ARIMA(1,0,1)模型,并且改进后的时变O-U均值回复模型对气温变化过程的拟合程度较好。此外,时变O-U均值回复模型在期货定价方面展现出了比传统O-U均值回复模型更好的预测精度。
在得到上述研究结论的同时,本文还提出一些展望。第一,虽然本文选取的三个城市的均值回复速度均适合ARIMA(1,0,1)模型,但这并不代表其他地区也同样适合这一模型,具体的论证需要后续研究跟进。第二,虽然本文以三个城市为例证明了时变O-U均值回复模型的拟合效果更佳,但三个城市均来自同一地区,这种空间局限性表明时变O-U均值回复模型在我国其他地区未必拥有同样的作用效果,具体情况需要通过进一步拓展研究进行论证。第三,以天气期货为代表的诸多天气衍生品具有良好的天气风险规避效果,并已经得到了国外资本市场20余年的检验,但是这一金融创新产品还未在我国成为正规的场内交易产品,希望有关部门可以尽快推动天气衍生品在我国证券市场的发行与流通,让这一产品真正帮助农户、企业以及整个农业对冲面临的天气风险。
参考文献
[1] Vasicek O.An Equilibrium Characterization of the Term Structure[J].Journal of Financial Economics,1977,5 (2):177-188.
[2] Dischel B.At last: A Model for Weather Risk[J].Energy and Power Risk Management,1998(1):78-86.
[3] Dornier F,Queruel M.Caution to wind.Energy Power Risk Management[J].Weather Risk Special Report,2000(1):30-32.
[4] Alaton P,Djehiche B,Stillberger D.On Modelling and Pricing Weather Derivatives[J].Applied Mathematical Finance,2002,9(1):1-20.
[5] Bhowan A.Temperature Derivatives[R].School of Computational and Applied Mathematics,University of Wiwatersrand,2003.
[6] Benth F E,Saltyte B J.The Volatility of Temperature and Pricing of Weather Derivatives[J].Quantitative Finance,2007,7(5):553-561.
[7]劉国光.天气预测与天气衍生产品定价研究[J].预测,2006,25 (6):28-33.
[8]李永,夏敏,吴丹.O-U模型在天气衍生品定价中的合理性测度[J].统计与决策,2011(21):32-35.
[9]李永,夏敏,梁力铭.基于O-U模型的天气衍生品定价研究:以气温期权为例[J].预测,2012,31(2):18-22+37.
[10]陈百硕,李守伟,何建敏,等.天气衍生品中时变均值回复的气温预测模型研究[J].管理工程学报,2014,28(2):145-150.
[11]王明亮,何建敏,陈百硕,等.时变O-U模型在气温预测及气温期货定价中的适应性研究:基于北京市1951—2012年的日平均气温数据[J].中国管理科学,2015,23(2):44-49.
