部分概率权重矩法和高阶概率权重矩法在洪水频率分析中的比较研究?剻?

李 扬

(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

设计洪水是估计水工建筑物抗御洪水能力和各种工程与非工程措施防洪效益的首要依据，实际工程设计中常需要估计重现期较长的洪水设计值。在一个年最大流量序列中，较小流量和较大流量往往不能同时拟合在某种概率分布曲线附近。为了照顾多数点据，拟合时常采用目估适线等方法，侧重拟合频率曲线的中下部，难以兼顾频率曲线的上部，往往导致重现期较长的大洪水估计精度不足。因此，国外研究者提出了针对重现期较长的大洪水段进行拟合的几种参数估计方法，基于Cunnane[1]首次提出的删失样本概念，Wang[2-6]推导了部分概率权重矩法(Partial Probability Weighted Moments, PPWM)、高阶概率权重矩法(higher-order probability weighted moments, HPWM)和高阶线性矩法(high-order L-moments, LH)的无偏估计量公式，其中，PPWM法与HPWM法均是基于概率权重矩法的改进参数估计方法。

近年来，国内研究者开始引入PPWM法、HPWM法及LH矩法进行洪水频率分析的研究。王怡璇等[7]研究了低删失样本下广义极值分布的部分概率权重矩，并应用于陕北地区主要水文测站的实测洪水序列拟合，取得了优于普通概率权重矩法的效果；原秀红等[8]对比了部分概率权重矩法与矩法在广义极值分布参数估计中的统计特性，结果表明基于部分概率权重矩法的估计量统计特性优于矩法。Deng[9,10]基于最小交互熵原理将PPWM法应用于删失样本极值分位数估计亦取得了理想的效果。由于部分概率权重矩的公式推导过程较为复杂，而高阶概率权重矩的推导和计算相对简便，笔者研究了广义极值分布的高阶概率权重矩[11]，而后推导了P-III分布的高阶概率权重矩及参数估计量公式[12]，应用于陕北地区年最大洪峰流量序列的拟合，结果表明高阶概率权重矩的统计特性良好，并且可以有效改善大洪水段的拟合效果；肖玲等[13]、胡素端等[14]应用高阶概率权重矩进行洪水频率分析的结果亦显示：高阶概率权重矩可较好地拟合序列中大洪水段的经验点据。周长让等[15]推求了广义Pareto分布的高阶概率权重矩并给出了估参方法，结果表明高阶概率权重矩法对超定量洪水系列的稀遇频率洪水段拟合效果较矩法好。此外，王俊珍等[16]和杨惠等[17]分别研究了高阶线性矩法在洪水序列和降水序列频率分析中的应用，结果表明高阶线性矩法对序列高尾部分拟合效果较好，可以降低设计值的估计偏差。

现有研究表明，这些新型参数估计方法在洪水频率分析中均取得了较为理想的效果，且优于矩法、概率权重矩法等常规估参方法，计算虽较常规估参方法复杂，但可以借助计算机程序简化计算过程。然而，现有研究多针对其中一种方法与常规估参方法进行对比，而对不同新型估参方法的横向比较则不多见。换言之，对于某实测洪水序列，究竟哪种新型估参方法的统计特性更稳定，估计精度更高，对序列较大值的拟合效果更为理想？同时，计算的复杂程度也是实际应用中选择估参方法时需要考量的因素。

因此，本文拟对同样基于概率权重矩法改进的PPWM法和HPWM法进行统计特性和实际应用的比较研究。采用蒙特卡洛试验，对这两种参数估计方法的统计特性进行研究和比较，并通过实例对其适用性及拟合效果进行检验，以期为实际应用中优选参数估计方法提供依据。

1 部分概率权重矩和高阶概率权重矩

设随机变量X的分布函数为F(x)=P(X≤x)，其概率权重矩(Probability Weighted Moments，PWM)的表达式为[18]：

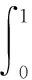
(1)

式中：r=0,1,2,…表示概率权重矩的阶数。若给定一个长度为n、服从F分布的样本，且x(1)≤x(2)≤…≤x(n)，其概率权重矩βr的无偏估计br可由下式计算：

(2)

广义极值分布(Generalized Extreme Value Distribution, GEV)是国内外洪水频率分析中广泛应用的一种概率分布[19]，其分布函数为：

(3)

式中：k为形状参数，k∈R；α为尺度参数，α>0；ξ为位置参数，ξ∈R。

当k≠0时，GEV分布的PWM为：

(4)

其无偏估计量br为：

(5)

1.1 部分概率权重矩(PPWM)

为有针对性地研究洪水序列较大值的拟合效果，在已知水文序列中选择大于某一门限值的观测值组成新的样本序列，该样本序列称为删失样本[20]，该门限值称为删失门限值。PPWM法的基本思想是给定不同的删失水平F0和与之对应的删失门限值x0，将小于x0的实测流量值从序列中去除，剩余较大实测流量值参与频率计算，删失水平F0=F(x0)，相当于序列中样本点的去除比例。因此，删失样本的部分概率权重矩可以在普通概率权重矩法的基础上进行扩充。将式(4)中F的积分区间由[0,1]变为[F0,1]，即可得到PPWM的表达式。当k≠0时，GEV分布的PPWM为

(6)

式中：P(-(r+1)lnF0，1+k)为不完全gamma函数，其表达式为：

(7)

可推出：

(8)

令：

(9)

给定不同k值，计算拟合z-k曲线k=a0+a1z+a2z2并求得曲线系数如表1。

可推求出各参数的估计量表达式为：

(10)

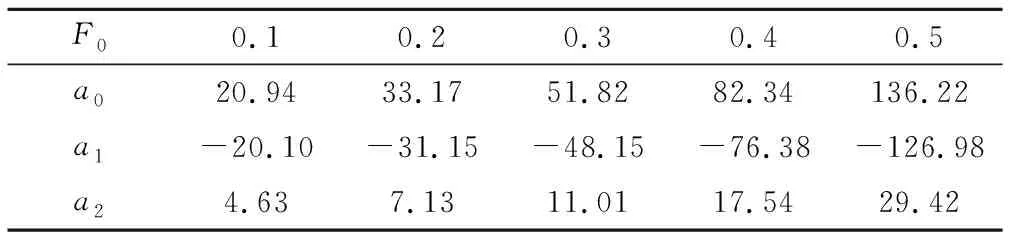
表1 不同删失水平下z-k曲线系数Tab. 1 Coefficients of z-k curves under different censoring levels

(11)

(12)

(13)

1.2 高阶概率权重矩(HPWM)

PPWM法中，通过定义删失样本，小于删失门限值的样本点被舍弃，从而不再影响分布的拟合效果。实际上，较小的流量值对拟合结果的影响十分有限，拟合效果的好坏仍主要取决于序列的较大值部分，因此，从概率权重矩的定义出发，通过提高PWM的阶数r为随机变量x赋予更大的权重，可以更加容易地实现侧重拟合序列较大值的目的，这也是HPWM法的基本思想。对k≠0，令r=η,η+1,η+2，可推出：

(14)

令：

(15)

给定不同k值，计算拟合z-k曲线，求得曲线k=a0+a1z+a2z2系数见表2。

表2 不同阶数下z-k曲线系数Tab. 2 Coefficients of z-k curves under different orders

可推求出各参数的估计量表达式为：

(16)

(17)

(18)

(19)

2 蒙特卡洛试验

2.1 试验方案

设置样本容量为100，模拟次数为N=10 000，给定位置参数的初值为ξ=0，尺寸参数的初值为α=1.0，形状参数为k=-0.5和k=0.5，部分概率权重矩的删失水平F0=0,0.1,0.2,0.3,0.4,0.5，高阶概率权重矩的阶数η=0，1，2，3，4。

2.2 评价标准

采用偏差(Bias)、标准误差(Standard Error,SE)和均方根误差(Root Mean Square Error,RMSE)3个指标，评价分布参数及设计值的估计值的无偏性和有效性。设计值的重现期选择了50年一遇、100年一遇、200年一遇和500年一遇。

偏差Bias反映了估计量与其数学期望的差距，Bias的绝对值越小，表示估计量的偏差越小，其无偏性也越好，其计算公式为：

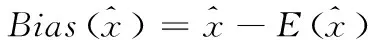
(20)

标准误差SE反映了估计量的有效性，对同一总体参数的估计量中，SE更小的估计量更有效，即SE的值越小，估计量的有效性越好。若统计试验次数为N，则SE的计算公式为：

(21)

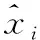
均方根误差RMSE是估计值与实际值偏差平方和与试验次数比值的平方根，用来衡量估计值与实际值之间的偏差，RMSE的值越小，表明估计的偏差越小，有效性越好。若统计试验次数为N，则RMSE的计算公式为：

(22)

2.3 试验结果

按照以上试验方案，用Matlab R2018a编程进行蒙特卡洛试验，结果如表3～表4及图1～图6所示。

可以发现如下规律：

(1)对于GEV分布的PPWM法(图1～图3)：①参数和各重现期设计值的估计偏差随删失水平F0的提高而增大，参数的估计偏差增幅较大，而设计值的估计偏差增幅相对较小；②各重现期设计值的估计偏差不随重现期的长度而改变；③无论k=-0.5还是k=0.5，参数估计的偏差均随删失水平的提高而显著增大，而设计值的估计偏差较小，k=-0.5时设计值估计的无偏性较好，而k=0.5时设计值估计的有效性较好；

(2)对于GEV分布的HPWM法(图4～图6)：①k=0.5时，随着概率权重矩阶数的升高，参数及各重现期设计值的估计值均接近无偏估计，显著优于k=-0.5时的情形；②k=0.5时，参数估计的无偏性和有效性均显著优于k=-0.5时的情形；

(3)两种估计方法对比：当k=-0.5时，GEV分布的HPWM法无论在参数估计的无偏性还是有效性方面都显著优于PPWM法，设计值的无偏性和有效性差距不显著，但HPWM法仍优于PPWM法。

表3 PPWM法蒙特卡洛试验结果Tab.3 Monte Carlo test results of PPWM method

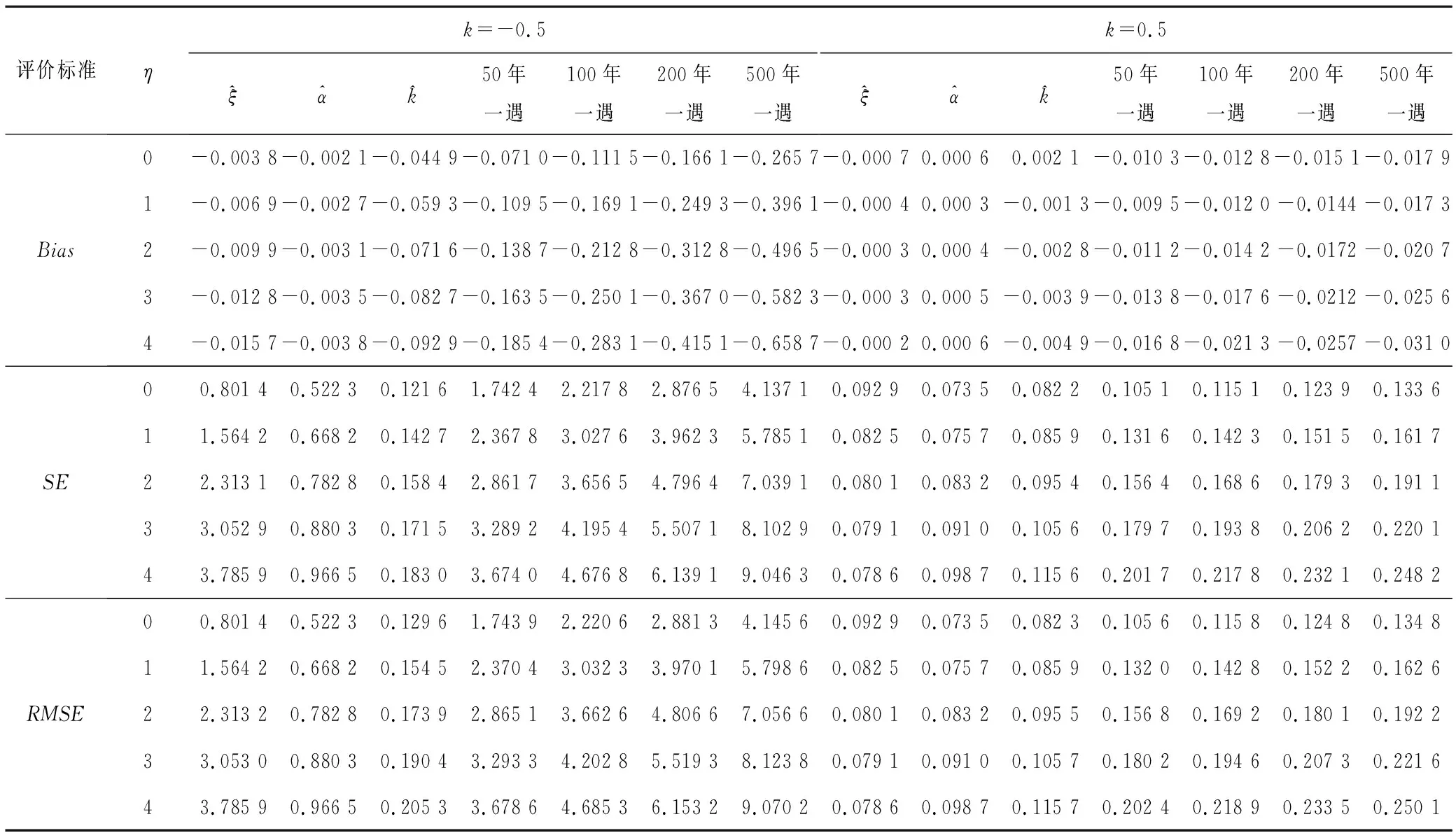
表4 HPWM法蒙特卡洛试验结果Tab.4 Monte Carlo test results of HPWM method

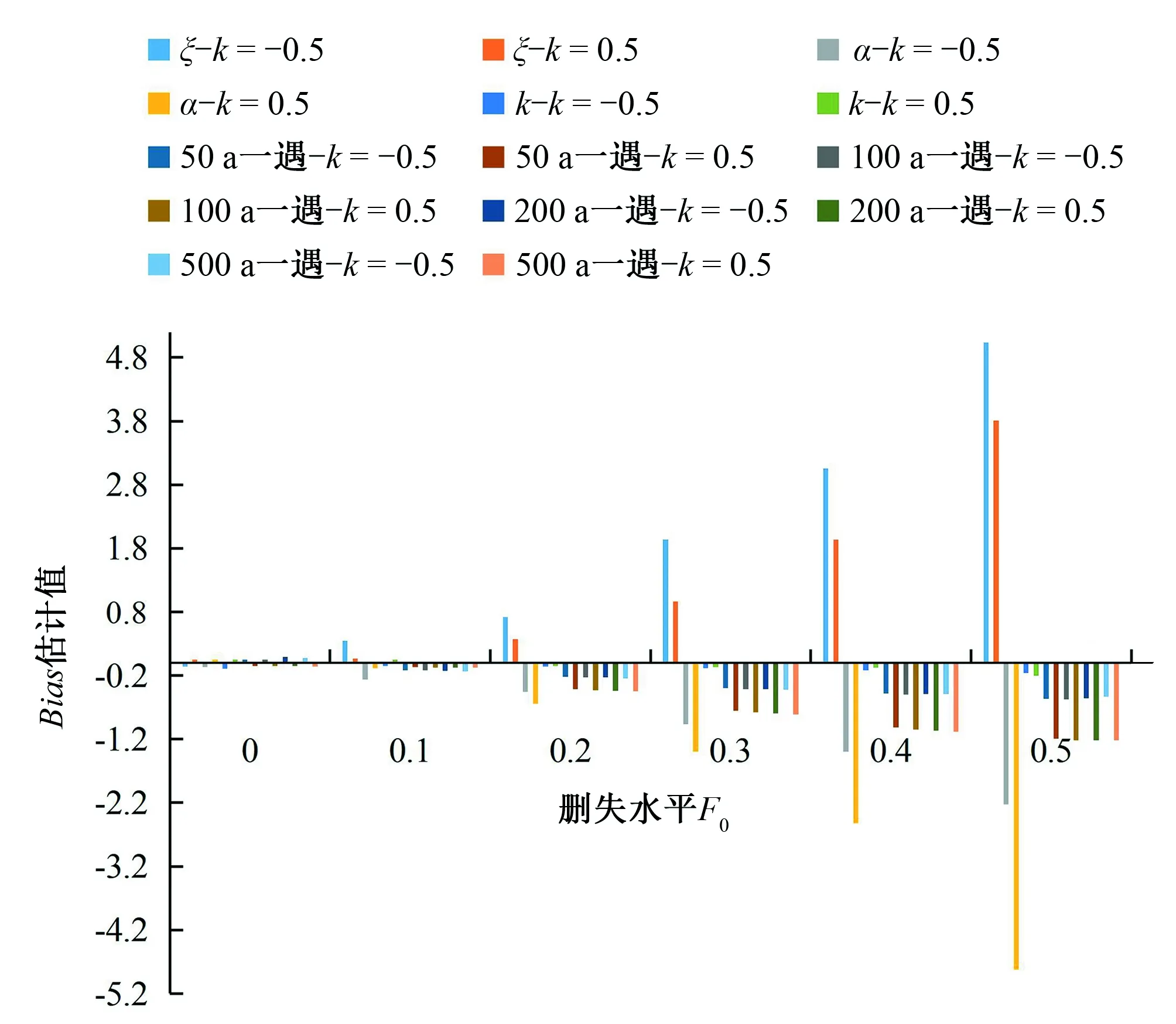
图1 不同删失水平下的PPWM法估计值BiasFig.1 Bias of PPWM estimators in different censoring levels

图2 不同删失水平下的PPWM法估计值SEFig.2 SE of PPWM estimators in different censoring levels

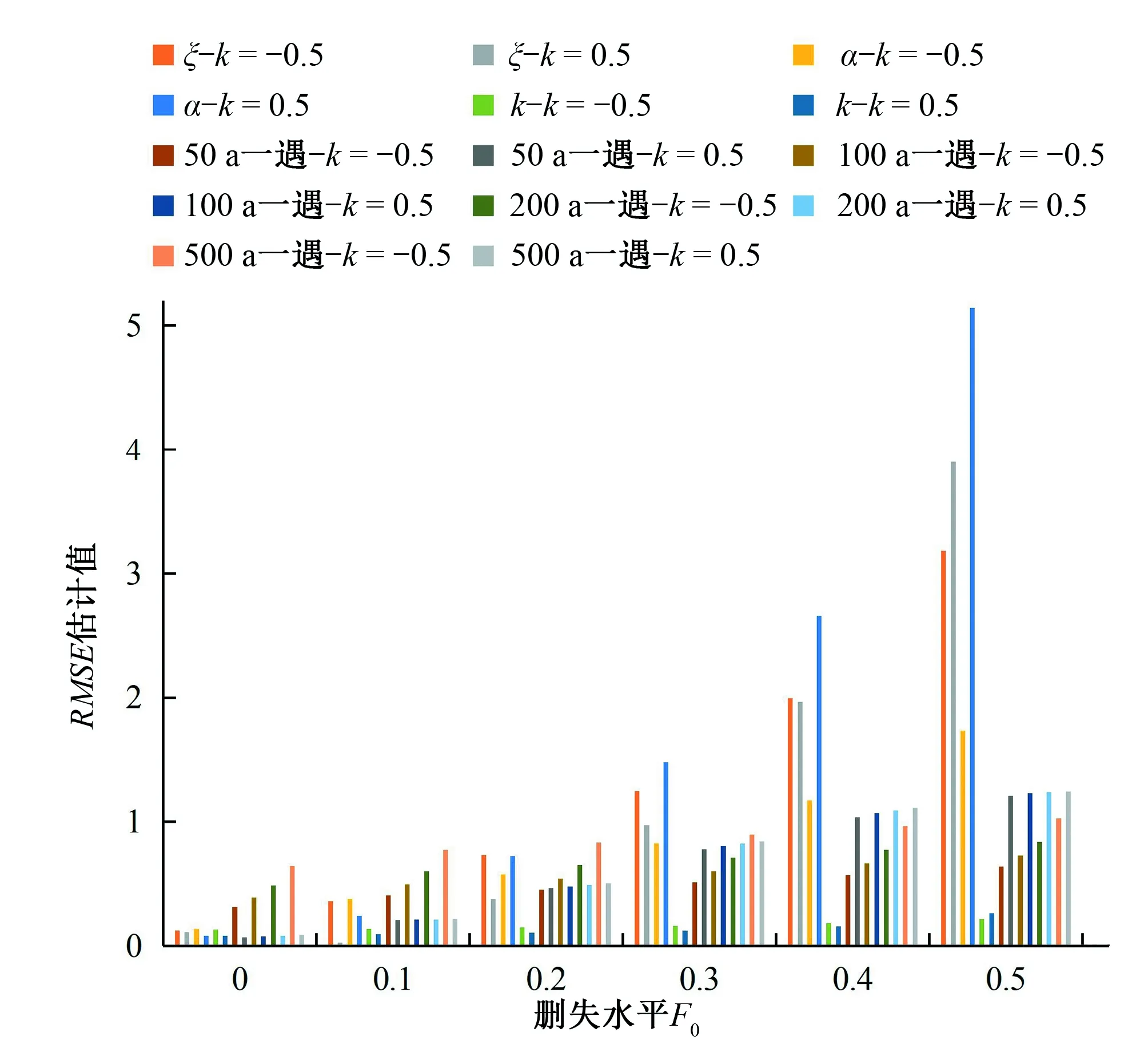
图3 不同删失水平下的PPWM法估计值RMSEFig.3 RMSE of PPWM estimators in different censoring levels

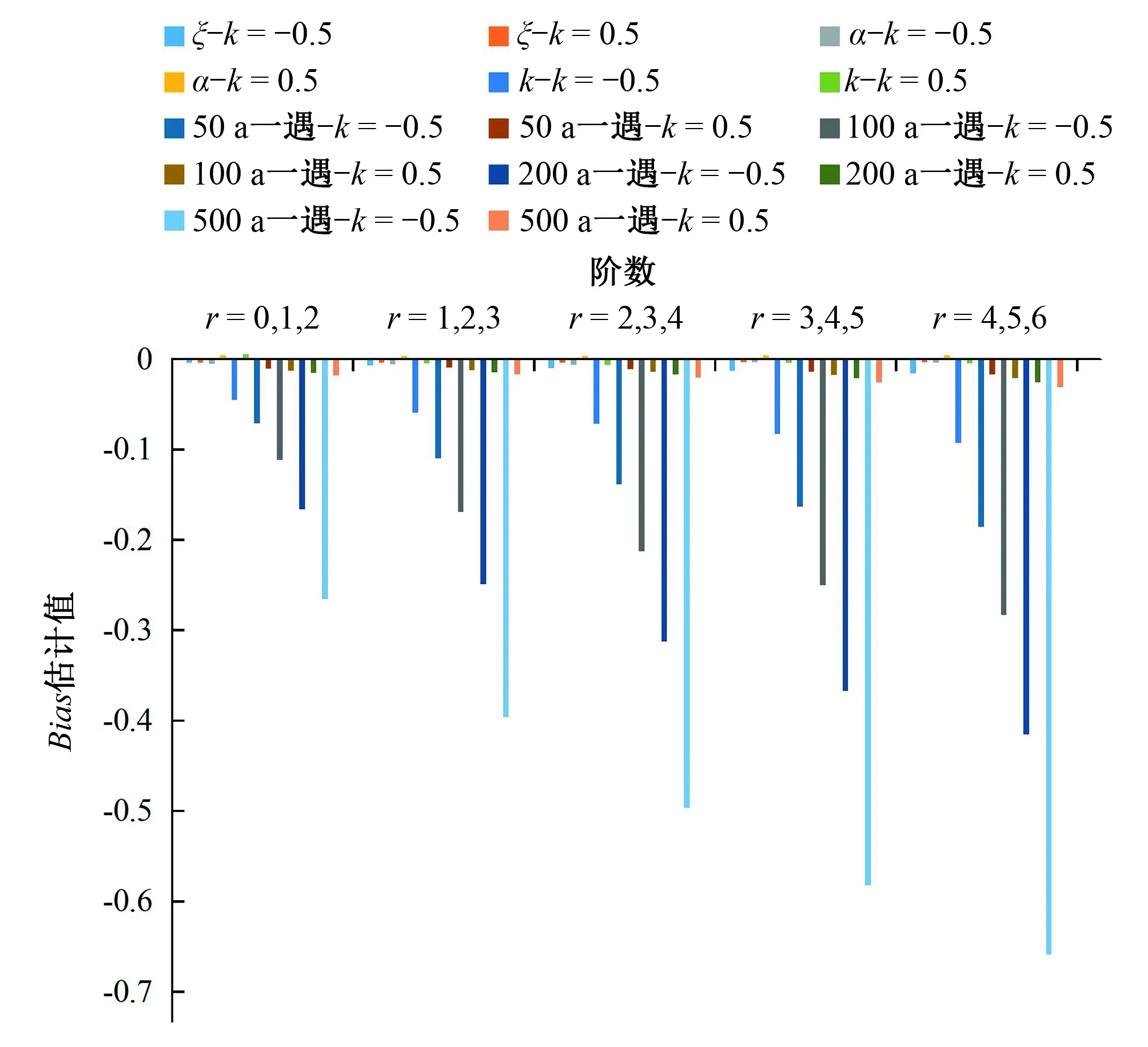
图4 不同阶数下的HPWM法估计值BiasFig.4 Bias of HPWM estimators in different orders

图5 不同阶数下的HPWM法估计值SEFig.5 SE of HPWM estimators in different orders

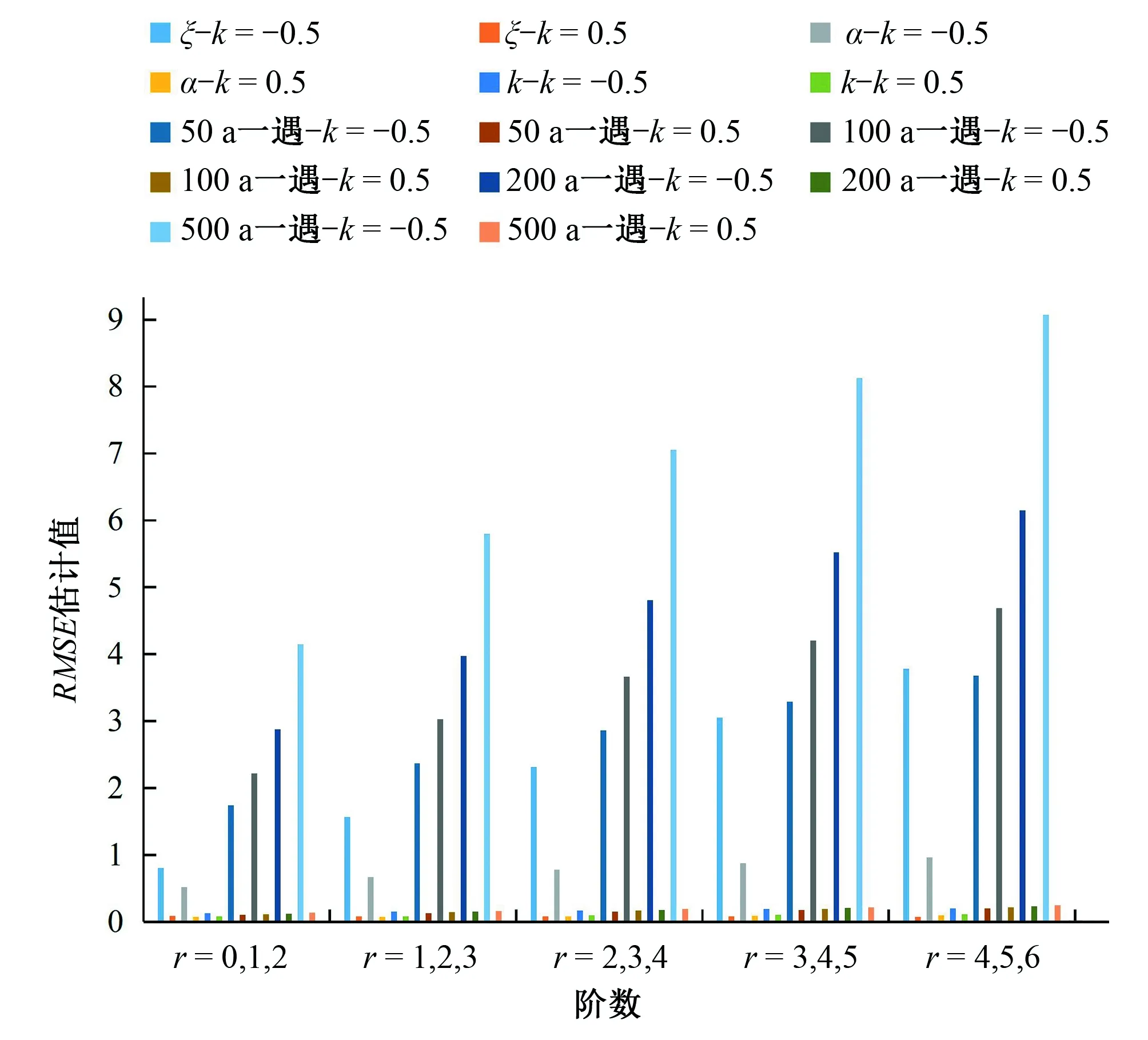
图6 不同阶数下的HPWM法估计值RMSEFig.6 RMSE of HPWM estimators in different orders

3 实例应用

3.1 资料及研究区概况

选用陕西省神木水文站1956-2003年的实测年最大洪峰流量系列资料，系列长度为48年。神木水文站位于陕西省神木县南郊，系黄河一级支流窟野河中游干流控制站，属于国家重要水文站，多年平均径流量4.888 亿m3，实测最大流量高达13 800 m3/s。窟野河流域地处黄河中游暴雨中心区，且水土流失严重，流域内洪水峰高量小、洪峰尖瘦、暴涨暴落，洪枯流量的变幅也很大，洪灾频发，对当地生产生活造成较大威胁，因此，在该站的洪水频率计算中，提高大洪水部分的拟合精度对当地的防灾减灾工作具有重要意义。

3.2 分布参数估计与频率曲线绘制

分别使用PPWM法及HPWM法，借助Matlab R2018a编程对GEV分布的参数进行估计，结果见表5。分别绘制PPWM法和HPWM法的频率曲线，如图7和图8所示，其中F0=0及r=0,1,2相当于普通PWM法。

3.3 拟合效果评价

由图7可知，采用PPWM法估计参数并拟合频率曲线时，随着删失水平F0的提高，实测序列较大值的拟合效果有明显改善，其中F0=0.4时，拟合效果最佳，F0=0.5时，拟合效果有变差的趋势。

由图8可知，采用HPWM法估计参数并拟合频率曲线时，随着概率权重矩阶数的提高，在序列较大值部分，理论频率曲线逐渐接近实测序列，在阶数为r=4,5,6时，拟合效果最优。

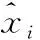
表5 GEV分布参数估计结果Tab.5 Parameter estimates of GEV distribution

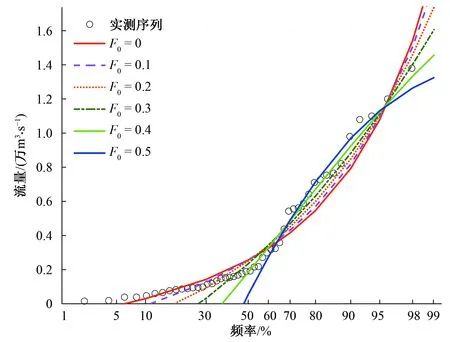
图7 神木站PPWM法频率曲线拟合结果Fig.7 Curve fittings for different censoring levels of PWMs

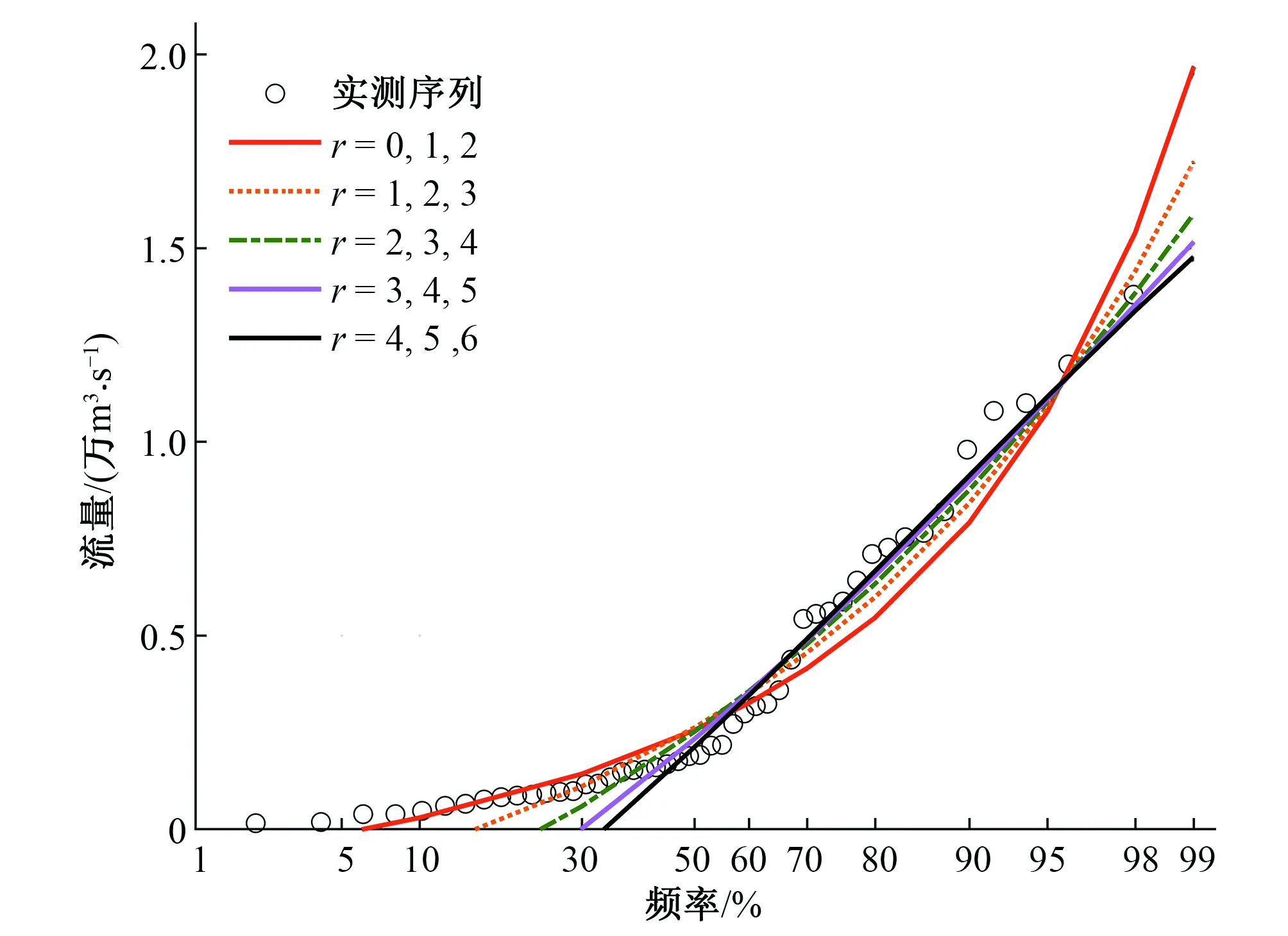
图8 神木站HPWM法频率曲线拟合结果Fig.8 Curve fittings for different orders of PWMs

(23)

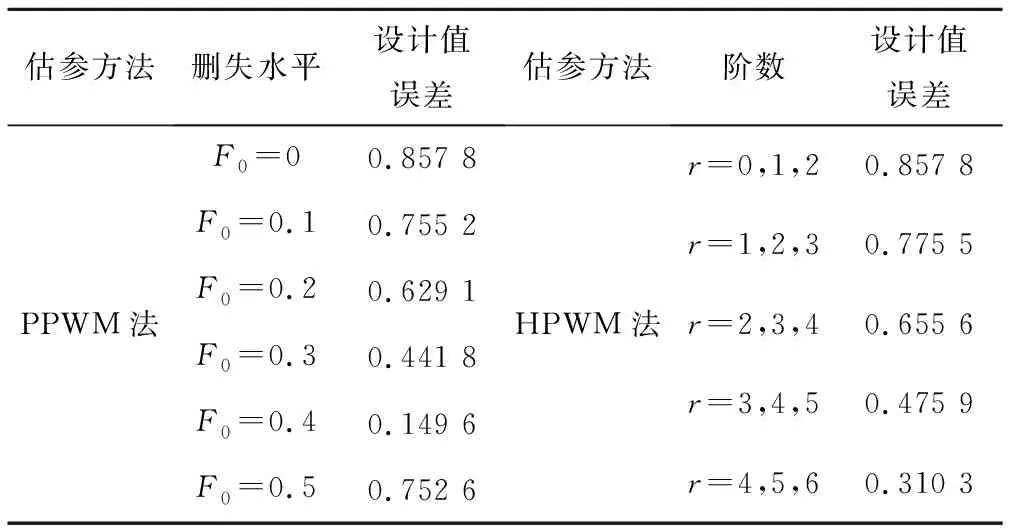
表6 神木站不同估参方法的设计值误差Tab. 6 Quantile errors using different methods in Shenmu station

为直观比较两种方法对同一序列较大值部分拟合效果的优劣，选择每种方法中拟合效果最优的参数组合，即F0=0.4和r=4,5,6的情况，单独绘制频率曲线(图9)进行对比。由图9看出，两种方法的曲线在P>50%时几乎重合，拟合效果不相上下，但HPWM法的曲线更接近最大实测值。

图9 神木站HPWM法和PPWM法拟合结果对比Fig.9 Comparison of Curve fittings of HPWMs and PPWMs

综合蒙特卡洛试验和实例应用的结果可知，HPWM方法的统计特性更加优良且稳定，实例应用中HPWM法和PPWM法的拟合效果基本相当，PPWM方法在P=60%～98%时的设计值的累积误差更小，可根据实际情况灵活选用。

4 结 论

现有研究表明，HPWM法、PPWM法、LH矩法等新型参数估计方法在洪水频率分析中均取得了较为理想的效果，且优于矩法、概率权重矩法等常规估参方法，其复杂计算可借助计算机程序得以简化。目前，国内对于这些新型估参方法的研究相对较少，且多为单一种类的新型估参方法与传统方法的对比研究，缺乏不同新型估参方法之间的横向比较。而在实际工作中，统计特性稳定、估计精度高、计算方便、能切实提高设计值估计精度、改善拟合效果的新型估参方法显然更容易实现推广应用。

PPWM法和HPWM法均为基于概率权重矩法改进的新型参数估计方法，均减小了实测洪水序列中较小流量值对拟合结果的影响。本文通过蒙特卡洛试验，对PPWM法和HPWM法的统计特性进行了模拟分析与比较，以国家重点水文站神木水文站多年实测年最大流量系列为实例，分别对两种方法的适用性进行检验，并比较两种方法的优劣。结果表明：在统计特性方面，HPWM法的无偏性和有效性均显著优于PPWM法，且估计结果稳定；在拟合效果方面，与普通概率权重矩相比，提高PWM的阶数(HPWM法)或增加删失水平(PPWM法)均可显著改善实测洪水序列的拟合效果，PPWM方法在P=60%～98%时的设计值的累积误差更小；在计算难度方面，PPWM法估计量公式推导及计算难度较大，HPWM法计算时仅需改变阶数，计算相对简便，而这两种方法对实例的拟合效果相当。

此外，笔者在此前的研究中发现[21]：HPWM法与PPWM法对陕北地区其他水文站年径流序列的频率分析结果均逊色于普通概率权重矩法，且PWM阶数越高/删失水平越高，拟合效果越差；洪峰流量偏小的站点，HPWM法和PPWM法对拟合效果的改善相对不显著。

综上所述，HPWM法与PPWM法估参均适宜用于洪水频率分析计算，且拟合效果基本相当，适宜用于洪峰流量较大的站点，在实际工作中更推荐使用计算相对简便的HPWM法进行频率分析。