珠江上中游社会-水文多因素的系统动力学生活需水预测
2020-11-23路岚青覃叶红萍
易 彬,陈 璐,路岚青,覃叶红萍
(1. 华中科技大学水电与数字化工程学院,武汉 430074;2. 数字流域科学与技术湖北省重点实验室,武汉 430074)
0 引 言
随着世界经济迅速发展、全球人口加速膨胀、城市化进程普遍加快,世界各地对水资源的需求日益增长。水资源短缺已成为影响世界政治格局、经济发展和社会进步的重要瓶颈问题,其本质在于供给和需求的矛盾和不平衡。联合国数据估计,人类的需水量在两个世纪间发生了深刻变化,自20世纪初期,全球用水量仅4 000 亿m3/a,到20世纪末期,已上升至39 000 亿m3/a。因此,考虑人口增长、经济发展、城市化进程等社会经济因素,开展系统深入的生活需水预测研究,对保障社会经济可持续发展具有重要的现实意义。
需水预测的方法主要有时间序列法[1,2]、回归分析法[3,4]、灰色系统法等[5]。在上述方法中,回归分析法较为成熟,已广泛应用于工程实践,但该方法预测效果依赖于原始数据的长度和可靠性,此外,该方法存在需水预测因子与需水量必须高度相关的局限[6]。针对上述缺陷,灰色系统法、人工神经网络法[7]等黑箱建模方法应运而生,但该类方法要求原始数据在时间尺度上呈指数变化规律,换言之要求数据总体上变化趋势一致,在量级上无大波动,不存在周期性、无序性和突变[8]。然而,实际中大多数需水预测因子呈S型增长[9],因此系统黑箱模型的预测结果往往偏大。系统动力学方法是现阶段常用的一种需水预测方法,该方法是在反馈控制理论基础上,用计算机仿真的手段研究社会经济系统与水资源问题之间关系的一种定量与定性相结合方法,适合处理长期性、周期性等问题。
为厘清社会经济发展与生活用水量的本质关系,研究引入了社会水文学基本概念,融合了自然、人口、经济、环境和人类意识等一系列影响因素,提出了耦合社会-水文多因素的生活需水系统动力学建模方法,辨识了影响生活需水量的关键社会经济因子,构建了社会-水文相关因子与生活需水量互馈耦合网络拓扑图,建立了生产需水系统动力学差分和微分方程组,实现了自然、社会双重驱动下的生活需水预测。
1 影响生活需水的主要社会经济因子辨识
人口规模、生活水平提高导致了居民收入、水价、节水意识的提升以及城镇化进程的加快,这些因素都会导致生活需水量的变化[10]。杨亮等[11]认为人口规模的扩大对水资源损耗的增长具有显著影响。张晓晓等[12]指出城镇人口每增加1万人,城镇居民生活用水量将增加20.91 万m3。因此本文将人口和城市化水平作为影响生活需水变化的重要因素。
此外,城乡居民收入水平与该地区的生活需水量也有密切关系,随着人们消费支出的提高,更多支出将转移到高耗水型消费行业,如伴随居住环境升级以及卫生习惯改善(人类的意识行为),城市居民用水需求在边际上出现递增趋势。冯业栋等[13]发现经济因素对居民用水量的影响远超预期;姚远[14]认为水价、人口及居民人均年收入是决定用水量的重要因素。
综上所述,研究把常住人口、城镇化率、城乡居民收入、节水意识、水价等作为影响生活需水量的重要因素。
2 影响生活需水量的社会经济因子演化规律解析
2.1 马尔萨斯-逻辑回归人口预测模型
马尔萨斯人口增长模型是一种经典人口预测方法,其表达式为:
P(t)=P(t0)er(t-t0)
(1)
式中:P(t)为时刻t的人口;P(t0)为初始时刻t0的人口;r为人口增长率。该模型认为人口将持续成指数增长,当t趋于无穷时,人口也趋于无穷。
事实上,随时间推移,一个地区空间、食物和生育能力会限制本地区的人口,以至于最终该地区人口会趋于稳定,人口增长存在一个阈值,因此,该模型已不再适用。
因增长率是变化的,人口变化过程可用数学公式描述如下:
(2)
求解得:
(3)
式中:N为人口增长阈值。
该模型为马尔萨斯-逻辑回归模型,本文采用该模型进行区域人口的预测。
2.2 Logistic曲线城镇化率预测模型
Logistic曲线估算法是现阶段最为常用的城镇化率估算方法,具体表达式如下:
(4)
式中:δ代表城市化率;C为积分常数;d为待确定参数。
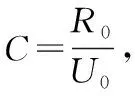
2.3 线性回归居民收入预测模型
城镇、农村居民可支配收入预测旨在探讨收入增加对居民生活用水需求的影响,选择线性曲线对地区城镇、农村可支配收入进行模拟,具体模型表述如下:
(5)
式中:RPIt、UPIt分别代表第t年时的农村、城镇居民人均可支配收入;RPI0、UPI0分别为研究基期t0的农村和城镇居民人均可支配收入;k1代表农村居民人均可支配收入增长率;k2代表城镇居民人均可支配收入增长率。
2.4 居民节水意识预测模型
随着经济增长,居民生活水平不断提高,对家庭生活用水的需求会增加,但在节水教育的普及下,居民素质不断提高,相应的生活需水量增量会放缓,主要驱动原因如下:① 居民家庭节水型器具使用量增加,导致用水量减少;② 培养好的生活用水习惯导致用水量减少(减少淋浴时间,减少洗涤剂用量);③ 合理重复利用生活用水导致用水量减少。相对于水价的提升对生活用水的影响,提高居民节水意识对生活用水量的变化更加明显。在此背景下,本研究提出了节水意识数学描述方法,有效模拟了节水意识对生活用水量的影响。
在理想状态下,假设节水意识K呈线性增长(0≤K≤1),节水意识年增长率θ保持不变,可用以下数学模型表示:
(6)
在实际生活中,居民节水意识实际增长过程是非线性的。近年来,居民素质上升明显,节水意识处于快速提升阶段,但这种提升并不是无节制的,到达一定程度时,上升速度会逐渐放缓,呈现出由快到慢的特征,并逐渐趋近于节水意识上限。基于上述分析,对节水意识数学模型做出如下定义:
(7)
式中:K代表节水意识;θ代表节水意识增长率;M代表节水意识上限。
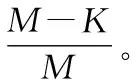
(8)
求解方程得:
(9)
具体确定步骤为:① 节水意识上限参数M的确定,M的取值范围为[0,1],首先设M=1;② 参数A的确定,对于基准年,t=0,根据式(9),K=M-A,假设A的取值在[0,M]之间,不同A值,则得到不同K值;③ 将不同K、M、A值代入需水预测模型,与历史需水量拟合误差最小的A值,即为所求。若当M=1时,无法拟合最优,可调整M的值,按照上述步骤,重新率定,直到拟合结果较优为止。
2.5 居民水价预测模型
水价是影响生活需水量的重要指标,城市水资源供需矛盾的凸显加剧了水安全危机,增强了水商品意识,通过水价的经济杠杆作用促进节约用水已经成为社会共识[15]。随着社会经济不断发展,生活用水水价呈现稳定上升趋势,研究拟采用分段线性函数模拟水价的变化过程,具体模型如下:
(10)
式中:PTi(i=0,1,2,…)代表Ti与前一时间节点间的水价均值。
3 耦合社会-水文多因素的系统动力学生活需水预测模型
根据建立的马尔萨斯-逻辑回归人口预测模型、Logistic曲线城镇化率预测模型、线性回归居民收入预测模型、节水意识预测模型,首先预测常住人口、城镇化率、城镇及农村人均可支配收入、节水意识的未来演化趋势;构建影响生活需水量的社会经济因素因果关系图(如图1所示),依据各变量的因果关系,建立耦合社会-水文多因素的生活需水系统动力学模型,模型表达式如下:
(11)
式中:ΔURWD、ΔRUWD、ΔDWD分别为城市生活需水增量、农村生活需水增量、生活需水总增量;DWDt代表第t年的生活需水量;DWDt-1代表t-1年的生活需水量;UPI代表城市居民人均收入;RPI代表农村居民人均收入;ΔURP代表城镇人口增加值;ΔRUP代表农村人口增加值;ΔTPK代表总人口增加值;Δδ代表城镇化增长率变化值;P代表生活用水水价;χ代表居民收入弹性系数;φ1代表农村人口增量调节系数,表示农村人口变化对生活需水的影响程度;φ2代表城镇人口增量调节系数,表示农村人口变化对生活需水的影响程度;φ1、φ2分别表示农村、城市生活用水水价弹性系数;K代表节水意识。
为进一步解析式(11)的物理意义,提取图1中主要因素对生活需水量的影响关系图,如图2(a)所示。历史研究表明,生活需水量与居民生活购买力系数(即居民可支配收入与生活用水水价的比值)存在显著相关性[16]。在此基础上,研究提出式(11)中第1、第2式,由图2可知,其表征了城市、农村生活需水增量 和 与城市人口增加值 (或城市化导致的农村人口减少值 )、人均可支配收入PI、生活水价 等多种因素的定量映射关系。由图2(a)可知,人口增量、人均可支配收入对生活需水量呈现正反馈态势,居民水价对生活需水增量呈现负反馈态势。通过式(11)可模拟多种因素对生活需水量改变的综合影响。式(11)中第3式表征了生活需水量总增量等于城市需水量增量加农村需水量的增量,为避免生活需水预测出现偏大趋势,研究以居民节水意识对城镇、农村生活需水增量进行修正,即节水意识加强,生活需水量增速变缓[如图2(b)所示],进一步,得到地区生活需水总增量。最后,根据式(11)中第4式通过第t-1年生活需水预测值和生活需水增量计算第t年生活需水量预测值。
4 实例研究
4.1 研究区域概况
本文以珠江上中游为例开展例证研究。珠江上中游由梧州站点以上地区组成,隶属于珠江水资源一级区。地处东经103°09′~111°40′北纬3°41′~26°49′之间,面积为30.43 万km2,珠江上中游包括南北盘江、红柳江、郁江、西江等水资源二级区。涉及区域大部在广西、云南、贵州省份,小部分在越南谅山,具体如表1所示。以下的研究的基准期为2007年。
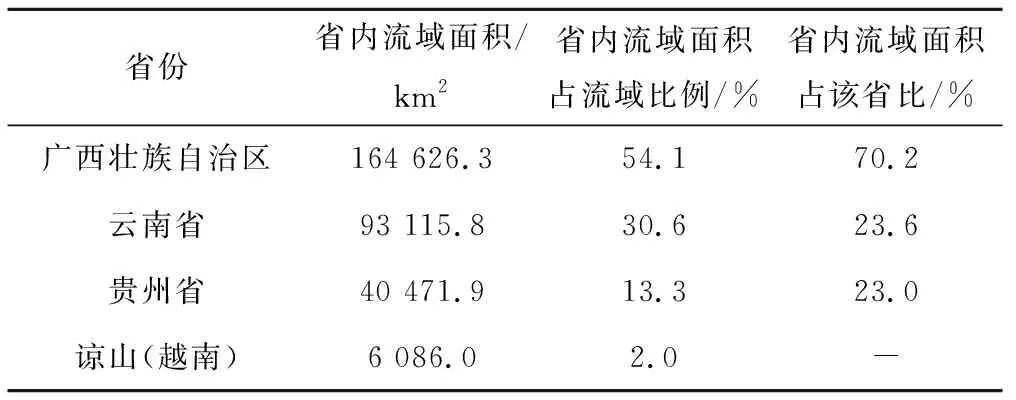
表1 珠江上中游涉及地区及面积比Tab.1 The area and area ratio of the upper and middle reaches of the Pearl River
4.2 影响生活需水量关键指标的预测
采用式(11)建立珠江上中游需水预测模型,分别采用所提马尔萨斯-逻辑回归模型、Logistic模型、线性回归模型、节水意识模拟函数、分段线性函数进行上述因子模拟,各模型参数列于表2。

表2 需水预测模型参数表 Tab.2 Parameter table of water demand prediction model
4.2.1 珠江上中游人口预测结果
珠江上中游地区人口采用马尔萨斯-逻辑回归方程预测,P(t0)为基准期人口数量,首先,参考各地区人口增长规划值确定研究区域人口自然增长率r;然后,假设不同的人口增长阈值,将人口自然增长率r、基准期人口数量代入模型,可得到人口预测值,以人口经验值与预测值拟合最优为准则,确定人口增长阈值N。综上,珠江上中游流域涉及广西、云南、贵州三省的人口自然增长率取值分别为0.8%、0.7%、0.8%;人口增长阈值根据人口自然增长率进行确定,其具体依据为人口自然增长率条件下,人口经验值与模拟值离差平方和最小,模型参数见表2,采用式(3)对珠江上中游的人口进行模拟,模拟结果及相对误差如图3(a)所示,可知,云南省和贵州省人口模拟值与实际值相对误差都在2%以内,广西模拟误差略大,但误差仍在5%以内。因此,人口模拟结果较好,该模型可用于未来人口演化趋势预测。
4.2.2 Logistic曲线城镇化率预测模型

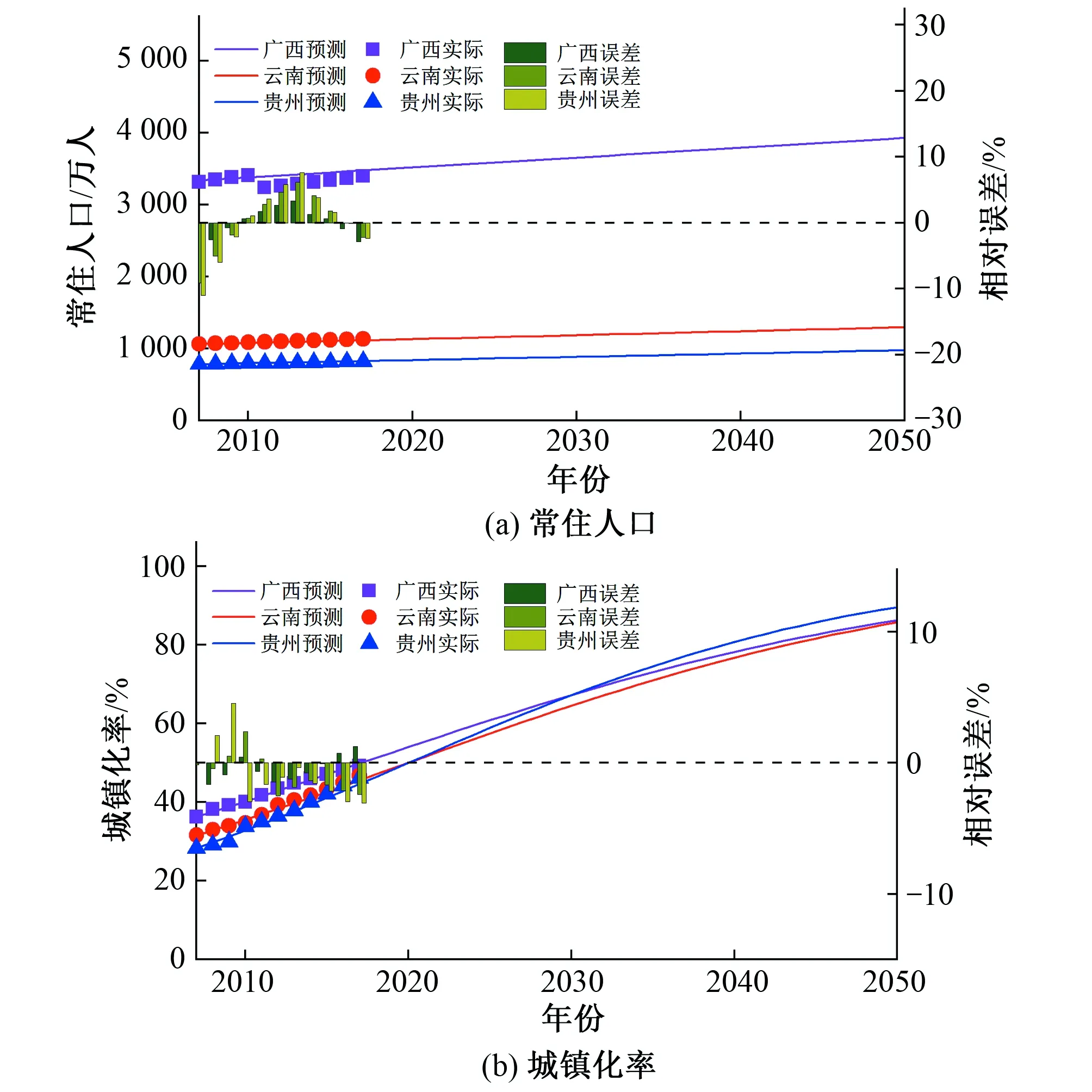
图3 珠江上中游流域人口和城镇化率模拟图Fig.3 Simulation diagram of population and urbanization rate in the upper and middle reaches of the Pearl River Basin
4.2.3 基于线性回归的居民收入预测模型
根据式(5),采用线性模型建立各省农村及城镇居民可支配收入预测模型,其参数采用最小二乘法确定,参数结果如表2所示,采用所建模型对珠江上中游流域各区域城镇化发展状况进行模拟,其模拟值与实际值及二者的相对误差见图4,由图4可知,所建模型与实测值拟合效果较好。
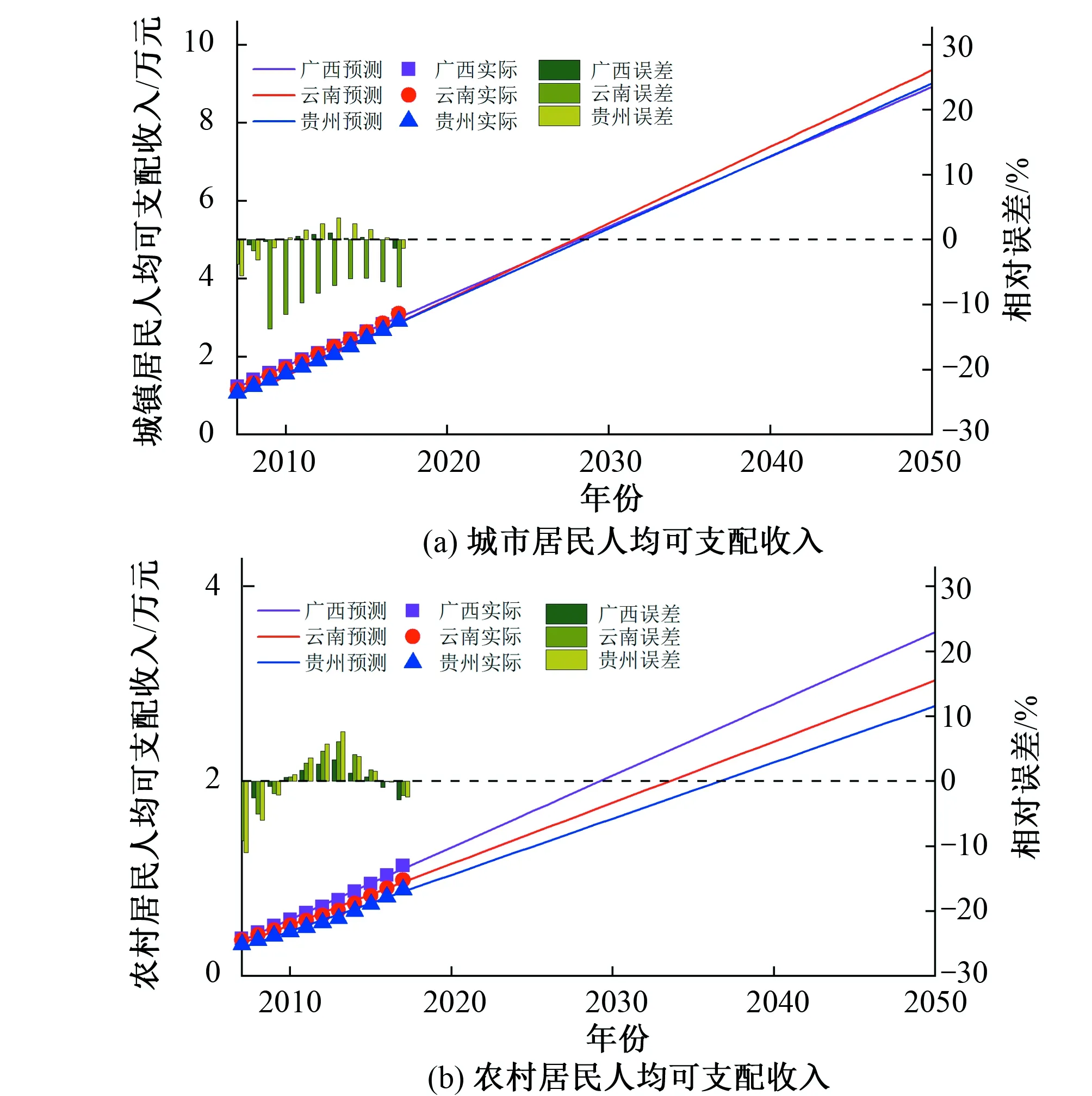
图4 珠江上中游流域农村、城镇人均可支配收入模拟图Fig.4 Simulation diagram of per capita disposable income of rural and urban areas in the upper and middle reaches of the Pearl River
4.2.4 节水意识预测模型
因各省需水增长趋势、经济发展水平、水资源富集程度不一,各省节水意识模拟结果也不尽相同。因节水意识无历史值可供参考,研究以试错法率定节水意识方程的参数值。由上述方法,确定的K、M和A值如表2所示。根据上述建的各省节水意识预测模型,对珠江上中游进行居民节水意识预测,预测结果如图5(a)。预测结果表明广西部分居民节水意识起点较低,2007年为0.35,但是增长速度较快,2050年,其节水意识达到0.85,超过云南、贵州两省;云南省、贵州省节水意识增长曲线类似,2007年,两省节水意识都在0.4,到2050年,两省节水意识都将达到0.8左右。从2007年到21世纪中期,随着国家综合实力提升迅速,国民素质提升较快,因此,节水意识在2030年之前增长较快,截至2030年,3个省节水意识基本达到0.6以上,2030年之后的20年间,居民节水意识仍在缓慢增长,到2050年,我国已经建成社会主义强国,各项发展趋于稳定,珠江上中游居民节水意识经过30年的发展达到中等偏上水平。
4.2.5 水价模拟
各省历史水价均值以该省典型市县水价为标准进行计算,其中广西、云南、贵州三省历史水价均值分别为2.55元、3.45元和2.7元,以社会经济发展节点2020、2030、2050年为水价变化节点,李翠梅等[17]发现节水效果并非随水价的上升稳定增加,当水价范围在3~5元之间时,节水量呈明显下降趋势,因此研究假定各时间分段间水价增幅为20%,各省水价格如表3所示。
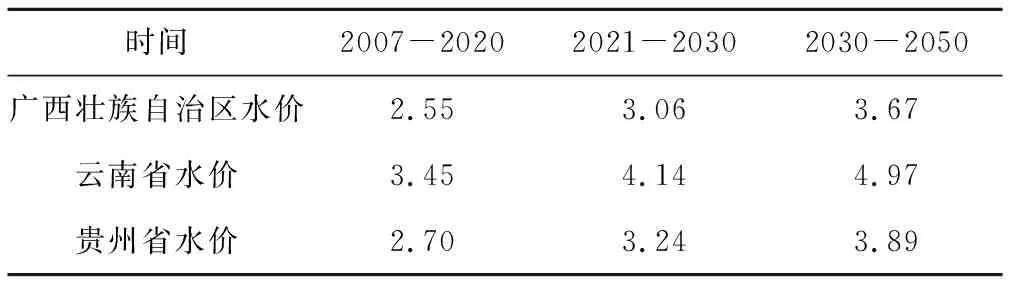
表3 珠江上中游流域水价格模拟 元
4.3 珠江上中游生活需水预测
本研究采用历史检验法验证需水预测模型的效果,将模拟值与真实值进行对比,计算两者相对误差。珠江上中游各省生活用水实际值和模拟值误差结果如图5(b)所示。检验结果表明,各地区模拟值和历史值比较有偏大趋势,各省生活需水的历史模拟总体误差在10%以内,个别年份误差超过该值,原因是各地区存在人口突变或者政策变更,导致的用水统计资料未能保持同步造成。因预测期长达30年,政策的变更均存在未知情况,仅能根据历史资料预测得到未来各因素的大体趋势,因此,模型的模拟结果可反映各省生活需水的发展和演化规律。具体地,珠江上中游流域生活需水总体呈上升趋势,但上升趋势不明显,珠江上中游地区未来生活需水增量较小,总体趋势平稳。其中,广西部分生活需水量由2007年的27.08 亿m3上升到2050年的31.33 亿m3;云南部分由4.71 亿m3上升至6.18 亿m3;贵州部分生活需水由3.57 亿m3增至5.55 亿m3。
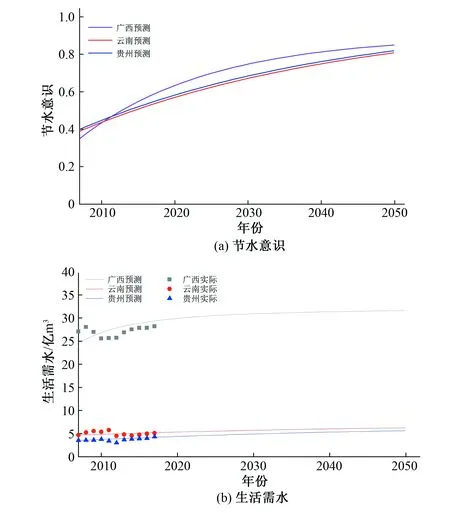
图5 珠江上中游流域各省节水意识和生活需水模拟Fig.5 Simulation of water-saving consciousness and domestic water demand in the upper and middle reaches of the Pearl River Basin
4.4 与现有模型的比较分析
用水配额法已广泛应用于生活需水预测研究中。研究分别采用用水配额法和所提系统动力学方法预测珠江上中游的生活需水量,结果如表4所示。预测结果表明,生活需水配额法在检验期,相对误差都为正值,由此可知预测结果系统性的高于实际值。经计算,用水配额法和系统动力学法的平均相对误差分别为5.16%和7.23%。因此,系统动力学预测方法的预测效果要优于生活需水配额法。
4.5 珠江上中游生活需水预测结果
综上,可以用上述生活预测系统动力学模型对珠江上中游地区进行生活需水预测,采用该模型模拟出2007-2050年的珠江上中游流域内生活需水量,2020、2030、2040、2050年的生活需水预测结果如表5所示。预测结果表明,2020-2030年10年间研究区域生活需水量增加了1.79 亿m3,2030-2050年20年间,生活需水增加1.61 亿m3,表明随着经济发展到一定程度,生活需水量不会随着人口的增加无节制增长,生活需水增长趋势会受到相关影响因素的制约而处于相对稳定状态,如科技的发展可以提高水资源利用率,水价的增长可以促进用水节约,国民素质的提高及居民节水意识的增强,都会一定程度降低生活用水量,这与我国发展规划相符,也和目前发达国家用水趋势一致。
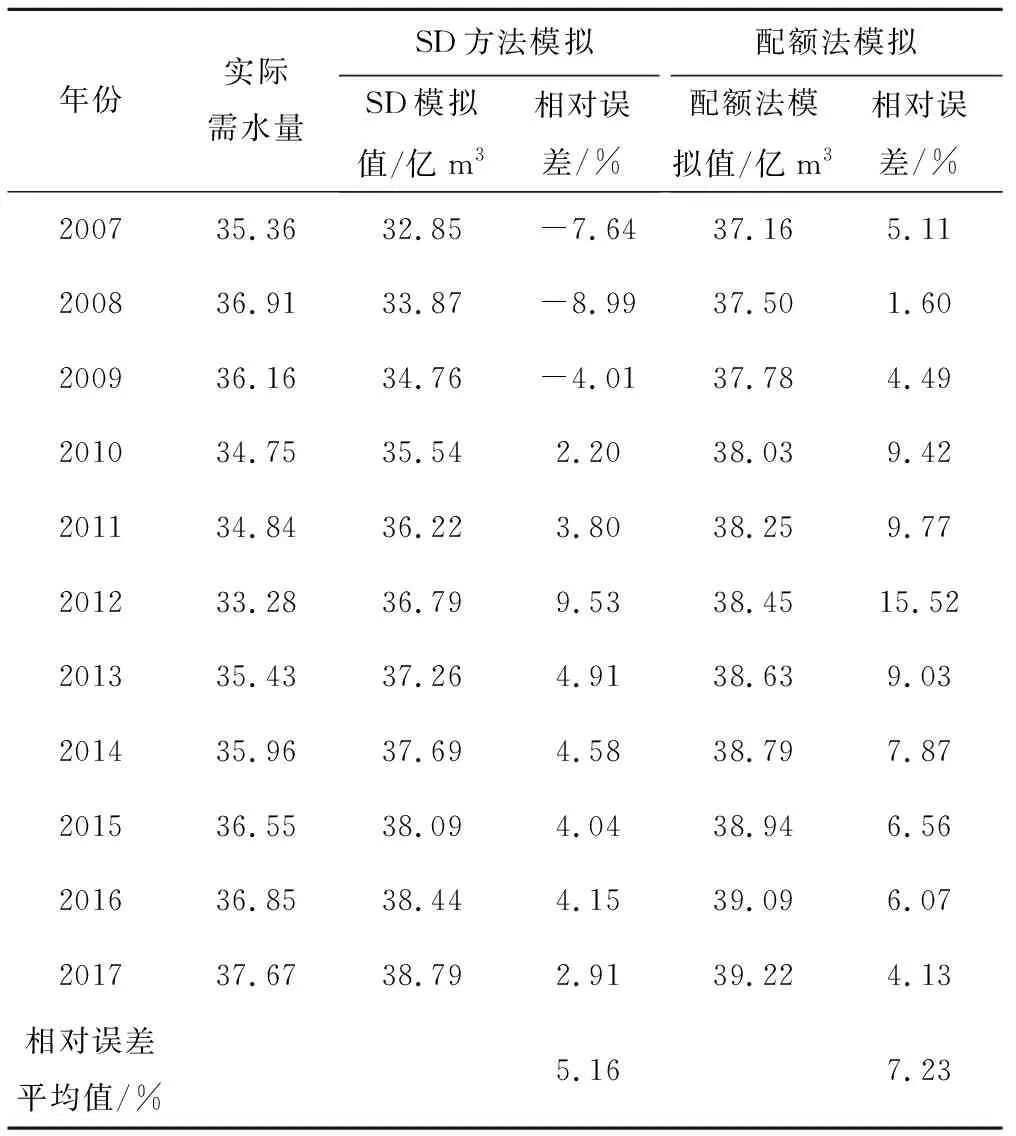
表4 配额法和系统动力学方法预测误差分析Tab.4 Prediction error analysis of quota method and system dynamics method

表5 珠江上中游未来生活需水预测值Tab.5 Forecast results of future domestic water demand in the upper and middle reaches of the Pearl River
5 结 论
研究提出了耦合社会-水文多因素的生活需水预测系统动力学方法,辨识了影响生活需水的关键社会、经济因子,揭示了人口、城镇化率、收入水平的长期演化趋势,首次提出了刻画节水意识演化规律的预测方程,在此基础上,建立了珠江上中游地区生活需水系统动力学模型。主要结果汇总如下:
(1)影响生活需水关键社会、经济因子预测结果表明,各因子历史值与模拟值拟合误差小,预测模型能较好反映珠江上中游地区的社会、经济和节水意识等的变化趋势。
(2)珠江上中游地区生活需水系统动力学模型预测结果表明,历史值与生活需水预测值较为接近,采用该模型进行未来生活需水预测是合理的,未来研究区域生活需水呈缓慢上升趋势,用水情势总体保持稳定。
(3)将所提方法与现有需水配额法进行比较分析,结果表明所提方法预测误差较小。
