基于遥感的秦淮河径流量估算方法

2020-11-23董增川王诗韵贾晴雯金大伟马嘉忆

中国农村水利水电 2020年11期

张璐，董增川，任杰，王诗韵，贾晴雯，金大伟，马嘉忆

(河海大学水文水资源学院，南京 210098)

河流水量计算在水资源规划、洪水预报、水利工程建设等领域有着广泛应用。通常情况下，河流水量数据可以通过水文测站获得，但是水文测站布局有限且部分地区径流资料难以实测，这些情况给洪水灾害管理、水资源调度等工作带来了很大困难。因此，探寻一种对实测资料依赖较小河流水量估算方法对于流域乃至全球河流水量监测具有十分重要的现实意义。

卫星遥感技术正在迅速的发展，其覆盖范围广且能快速的获得地表水资源相关信息，具有实时性、宏观性、周期性和费用低等特点[1]。因此，利用卫星遥感技术进行河流水量估算可以减少对实测资料的依赖，对缺乏水文测站地区水资源规划等工作提供了便利。国内外学者先后尝试利用遥感数据提取河宽、水位等对水量进行估算。Smith等[2]利用SAR卫星图像获取辫状冰川河流的有效宽度，利用河宽与流量的关系估算河流流量，证明了这种新的流量估算方法具有极大的潜力。Jung等[1]人利用 Landsat7 遥感影像提取水体，得到河宽后结合实测的河床断面获取过水断面面积和水力半径，代入曼宁公式估算河流流量，减少了这种估算方法的误差。Kouraev等[3]利用T/P测高数据估算鄂布河流量，通过实测流量与卫星资料的对比分析验证的测高数据流量估算的准确性。姚晓军等[4]以龙巴萨巴湖为例，利用GIS技术对1977-2008年不同年份的遥感影像进行数字化，构建冰碛湖库容-面积计算公式。Ling等[5]利用61景HJ遥感图像提取了荆江江段三个江心洲的面积与周边水文站实测流量构建关系曲线，并验证了方法的有效性和精度。这些方法表明了利用遥感图像估算水量的可行性，为缺乏水文实测资料地区水量的获取提供了多种方法。可是无论是利用遥感图像提取河宽或是水位，这种细微的变化虽然可以通过非常高分辨率的遥感图像来监测，但由于这种高分辨率遥感图像成本高、时间分辨率低，在这种情况下利用河宽和水位来推测河流水量是很困难的。用面积估算的方法以往的研究中多为利用湖泊面积进行库容估算，较少在河道水面面积进行水量估算方面进行深入探索。

选取秦淮河流域为研究区，以Landsat影像为数据源，利用ENVI提取整个流域水面面积，构建了一种具有良好精度的河流水量遥感估算方法。

1 数据来源与方法

1.1 研究区

秦淮河位于江苏境内，地处长江下游南京河段南岸，介于118°39′E～119°19′E，31°34′N～32°8′N之间。干流长约34 km，流域集水面积2 631 km2。秦淮河流域是一个构造盆地，呈扇形，被山丘环绕。流域位于亚热带半湿润季风气候区，多年平均降雨量为1 108.80 mm，降雨量丰富，流域平均径流量为6.95 亿m3。秦淮河有南北两水源，南源为溧水河，北源为句容河。在江宁区西北村漂水河和句容河汇合成秦淮河干流。在江宁东山镇秦淮河干流又分为两支河流，最终这两支河分别从流域西北角的武定门和秦淮新河两出水口流出，汇入长江[6-8]。

1.2 数据来源与预处理

选用1999-2016年Landsat-7和Landsat-8的遥感影像，空间分辨率为30 m，重访周期16 d，数据来源于地理空间数据云(http:∥www.giscloud.cn)。径流量资料来源于长江下游干流区(巢湖、青戈江水阳江、滁河、秦淮河水系)水文年鉴：秦淮新河站闸(118°40′E，31°58′N)、武定门闸(118°51′E，32°02′N)。对覆盖流域的遥感图像进行预处理(辐射定标、大气校正、几何校正以及去云处理)，以获取真实地物光谱反射，纠正图像变形，并保证地物识别的结果的准确性。

1.3 研究方法

1.3.1 构建水面面积-径流量曲线

选取覆盖秦淮河流域的Landsat-8或Landsat-7遥感数据影像，鉴于冬季河流存在结冰和浮冰等不利于研究的情况以及秦淮河水量的年内分配，遥感影像选择4-11月间云量较少的进行研究(这一时期秦淮河流量相对较大，遥感图像中水体边界清晰，进行水面面积提取的结果更加准确)。获取秦淮河流域的DEM数据，用ArcGIS提取流域边界[9]，利用所得到的流域边界裁剪预处理后的遥感影像，作为最终用来提取水面面积的秦淮河流域遥感图像。运用监督分类方法对秦淮河水体信息进行提取。

提取水面面积步骤：①选取水体训练样本。在流域水体的提取中，将地物要素信息分为水体和其他两大类。在秦淮河流域影像范围内选取足够数量的水体训练样本，以克服偶然因素对结果的影响, 并保证训练样本在研究区内均匀分布且具有代表性和典型性[10]。②计算样本可分离度。在选取训练样本后，利用ENVI软件中的compute ROI separability工具，计算每个感兴趣区组合的Jeffries-Matusita距离和转换分离度，两参数取值范围均在0与2.0之间，若样本为合格样本即所选取样本分离度较好则两参数均会大于1.9，而当参数值小于1.8时，样本分离度较差则需要重新选取水体的训练样本[11]。③执行监督分类。有6种分类器常用于监督分类(平行六面体、最小距离、马氏距离、最大似然、神经网络和支持向量机[12])，选取最大似然值法进行监督分类。④进行精度验证。Kappa系数可以反映分类结果图的分类精度，定义如下：

(1)

式中：K为Kappa系数；N为水体训练样本总数；Ppi为某一类水体样本所在列总数；Pli为某一类水体样本所在行总数。

Kappa系数与分类精度有如表1所列的关系[13]。Kappa系数大于0.6可认为分类精度较好，否则重新选取样本提取水面面积。

表1 分类质量与Kappa统计值Table.1 Classification quality and kappa statistics Kappp

计算流域水面面积。已知秦淮河流域总面积2 631 km2，根据ENVI监督分类后所得的水体面积占整个流域面积比值得到秦淮河流域的水面面积。

构建秦淮河水面面积-径流量曲线，用线性、指数、多项式和对数四种线型进行拟合，当相关系数大于0.75时，认为水面面积径流量具有较强的相关性。

1.3.2 选取最优估算模型

利用相关系数对不同线性所得到的估算模型进行初步分析。

用相关指数R2来说明模型估算准确性，R2值越大，估算模型的拟合效果越好；R2值越小，模型的拟合效果越差；R2越接近于1, 则表示回归的效果越好[14]。R2大于0.75，表示模型拟合度高，可解释程度较高；R2小于0.5，表示模型拟合度低，不宜采用。

残差平方和(RSS)为实测径流量与模型估算径流量之差的平方和，定义如下：

(2)

R2为年径流量回归平方和与其总离差平方和的比值，定义如下：

(3)

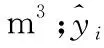
利用AIC和BIC准则进一步比较。

AIC识别准则(赤池信息准则)和BIC识别准则(贝叶斯信息准则)为两种较为常用的模型选择方法[15]。

AIC 准则和BIC准则定义如下：

AIC=2k-2ln(L)

(4)

BIC=kln(n)-2ln(L)

(5)

式中：k为模型的参数个数；n为样本数量；L为似然函数。

AIC值和BIC值越小，表明模型拟合效果越好。

根据比较相关系数、AIC和BIC值的综合结果选定最适合秦淮河的径流量估算模型。

1.3.3 验证模型精度

选取一定长度时间序列径流量数据带入所选择最优模型，利用实测径流量与模型估算径流量线性相关性验证模型精度，R2大于0.75时，认为模型估算的结果具有较好的精度。

2 结果与分析

2.1 年径流量拟合结果与分析

选取水文年鉴中2007-2016年秦淮新河闸和武定门闸年径流量，结合对应年份遥感图像的提取水面面积以此构建水面面积-年径流量曲线，得到秦淮河流域年径流量估算模型。

用线性、多项式、对数和指数4种线型进行拟合，如图1所示多项式和指数拟合结果较好，R2均大于0.75，证明秦淮河流域的水面面积与年径流量间具有较强的相关性。线性与对数模型的R2均小于0.5，不宜用作秦淮河年径流量评估。

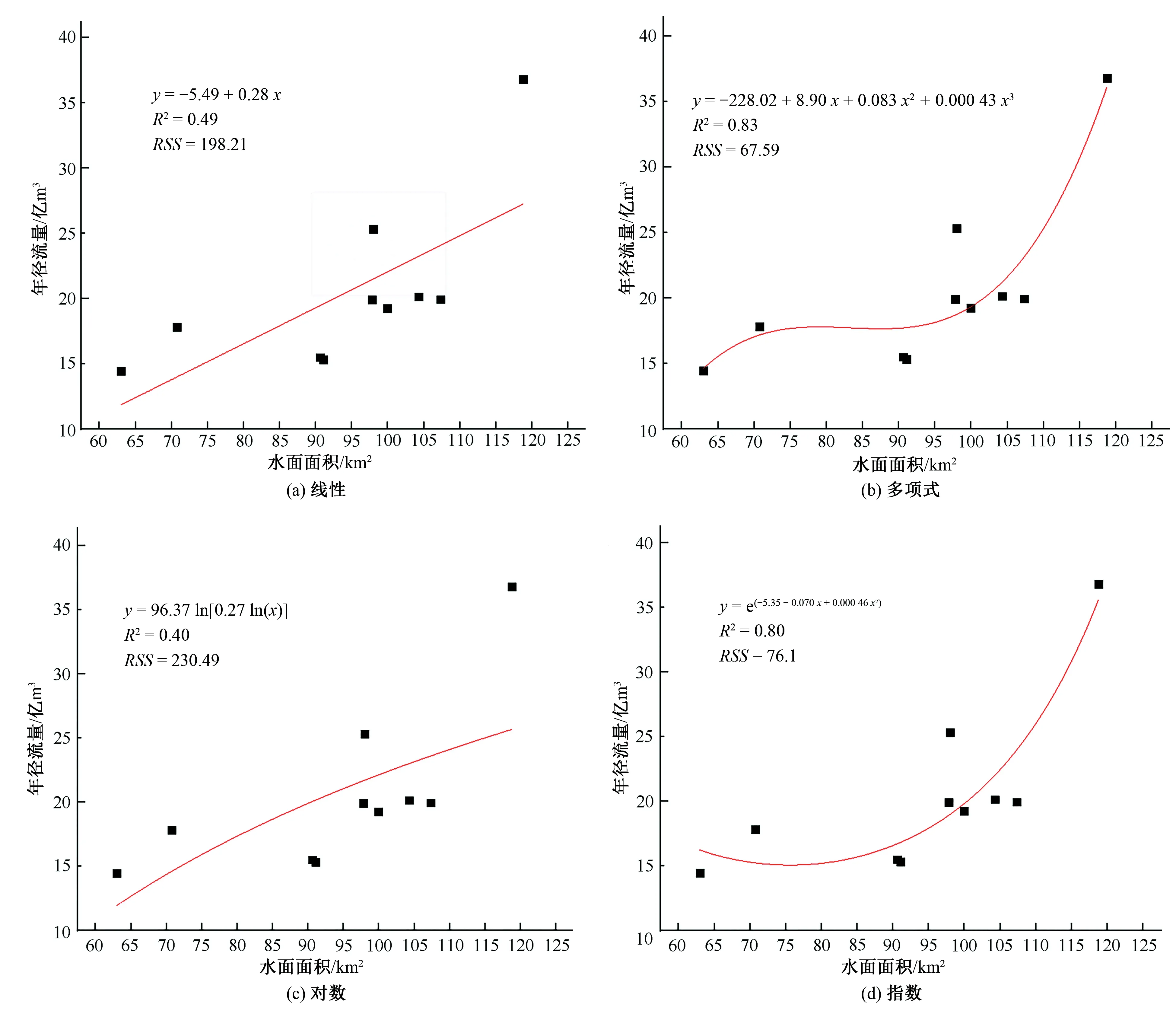
图1 不同线性拟合结果Fig.1 Different linear fitting results

利用AIC和BIC准则对多项式和指数的年径流量估算模型进一步比较，所得各项参数值见表2。

表2中指数模型的AIC和BIC值均小于多项式模型，两者Akaike权重分别为0.020和0.98，表明指数的拟合的结果相较于多项式有50.06倍的可能性是正确的。

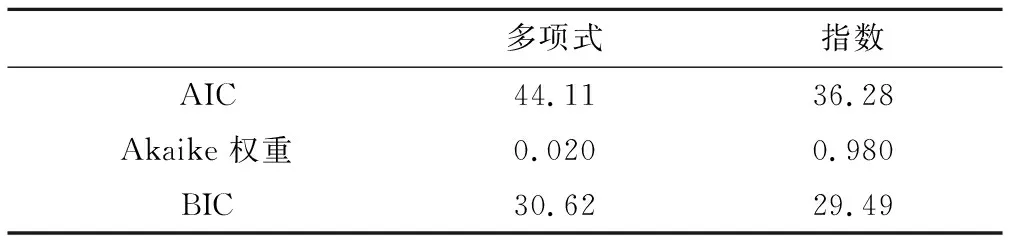
表2 AIC和BIC准则参数值Tab.2 AIC and BIC criteria parameter values

指数和多项式模型R2较为接近，但AIC和BIC的判断表明指数模型更加适用，因此将Q=e5.35-0.070 A+0.000 46 A2作为秦淮河年径流量估算方程，其中Q表示年径流量，A表示流域水面面积。

提取秦淮河1999、2000、2002、2003和2006五年的水面面积作为验证样本，检验指数模型精度。如图2所示，所得估算年径流量与实际年径流具有较强的线性相关性(R2>0.75)，证明指数模型应用于秦淮河年径流的估算具有较好的精度。

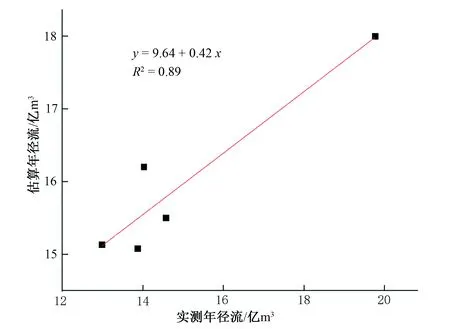
图2 年径流量模型精度验证Fig.2 Accuracy verification of annual runoff model

2.2 月径流量拟合结果与分析

利用2013-2015年期间24个月的数据，构建月尺度的水面面积-径流量曲线，分别用线性、指数、多项式、对数4种线型进行拟合。

如表3所示，水面面积与月径流量之间具有较强的相关性(R2>0.75)，且指数和多项式模型均可比较准确的表达两者关系，利用AIC和BIC准则对两个估算模型进一步分析，选取最优估算模型(表4)。

表3 月尺度曲线拟合结果Tab.3 Monthly scale curve fitting results

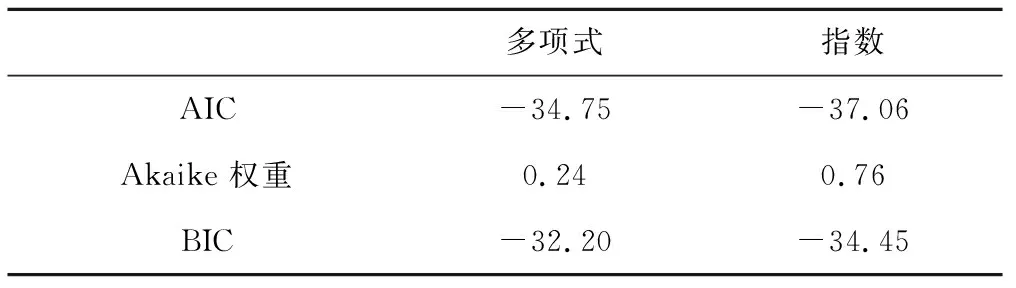
表4 AIC和BIC准则参数值Tab.4 AIC and BIC criterion parameter values

指数模型具有较小的AIC和BIC指，Akaike权重分别为0.24和0.76，表明指数的拟合的结果相较于多项式有3.17倍的可能性是正确的，因此指数模型同样也更加适用于月尺度的径流量估算。

提取2011-2010年期间12个月的水面面积作为样本验证月尺度模型精度。

指数模型估算年径流量与实际年径流具有线性较强相关性(R2>0.75)，证明Q=e-3.45+0.052 A-1.37×104 A2应用于秦淮河月径流的估算精度较高。

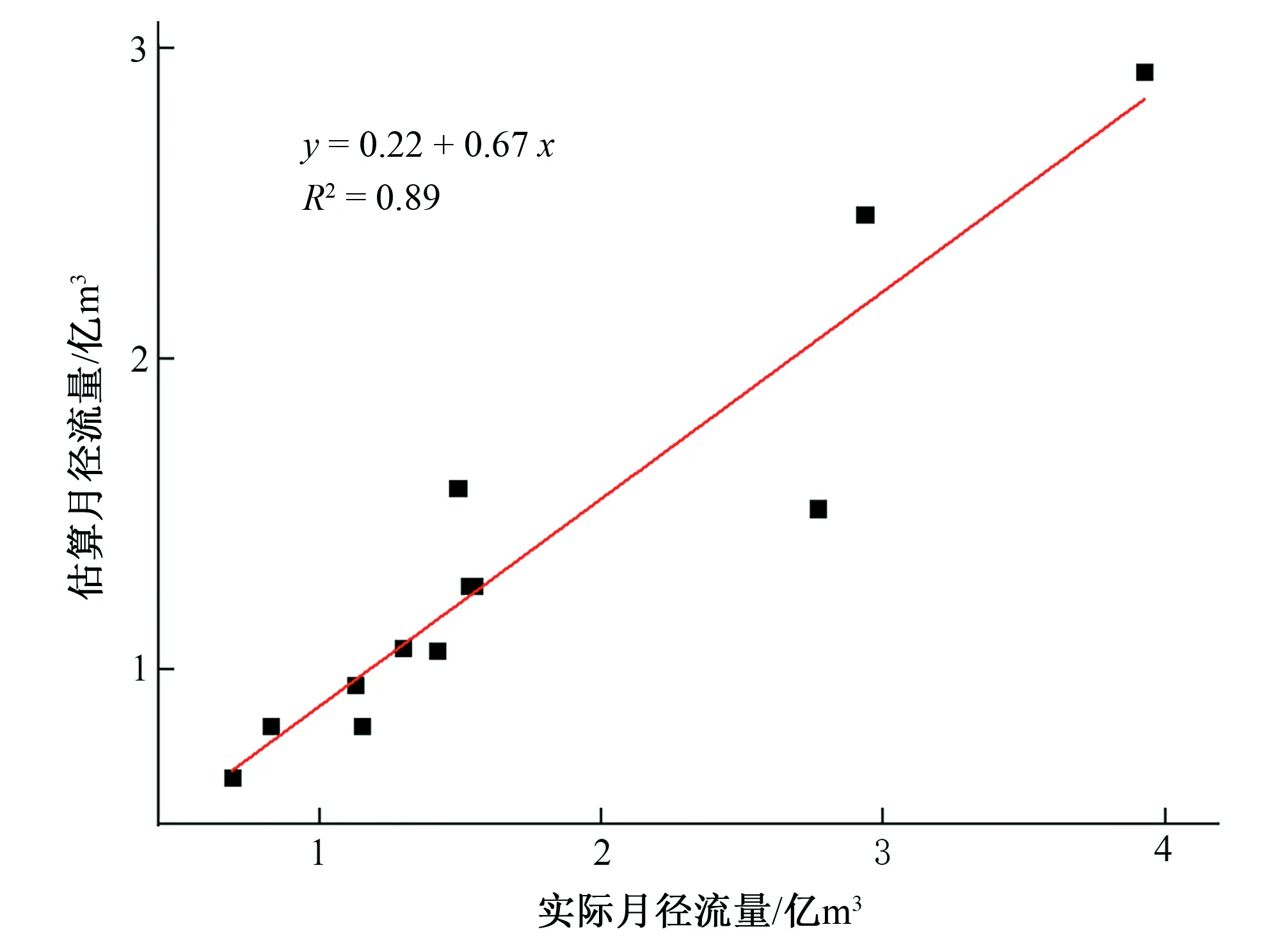
图3 月尺度模型精度验证Fig.3 Monthly scale model accuracy verification

河道横断面形态多呈发育不全的V形、梯形等形状，因此河道径流量的增减会引起河流水面面积的变化，秦淮河水面面积与径流量较好的相关性也进一步论证了用水面面积估算河流径流量的合理性。通过分别对不同线性的秦淮河年尺度和月尺度的估算模型进行对比分析，得到指数估算可最为准确的表述秦淮河水面面积与径流量的关系且适用于不同时间尺度的径流量估算，因此将秦淮河流域径流量估算模型定义为Q=e(1+b A+c A2)其中a、b、c为常数随时间尺度不同而变化。由于年尺度模型所用数据为年内数月的平均面积与相应的年径流量，而在月尺度模型中当月的水面面积变化与其月径流量变化会具有更密切的关系，因此相较于年尺度，月尺度模型普遍具有更高的相关系数，以此可以推断出模型的时间尺度的会影响估算精度，且时间尺度较小的月径流量估算模型精度更高。